| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
+20n.naoufal sadaso maths-au-feminin Hamouda geom Azerty1995 yasserito helloall Mehdi.A Mehdi.O Meded l'intellectuelle yasmine boubou math konica Nayssi az360 expert_run upsilon ali-mes 24 participants |
|
| Auteur | Message |
|---|
geom
Maître
 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Mer 29 Juin 2011, 10:56 | |
| | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Mer 29 Juin 2011, 12:07 | |
| | |
|
| | |
maths-au-feminin
Maître
 Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 16:55 | |
| probleme 33: soit A et B deux points du plan P tel que AB=5 détermine les ensembles suivantes   .(%20-\overrightarrow{MA}+6\overrightarrow{MB})=0%20\right%20\|%20\right%20\}) | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 17:36 | |
| Ton exercice nécessite des connaissances hors-programme de TC (barycentre), mais en tous cas je vous propose ma réponse: Ma réponse pour problème 33:- Spoiler:
Et je n'ai pas de problèmes à vous proposer... | |
|
| | |
maths-au-feminin
Maître
Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 17:50 | |
| - ali-mes a écrit:
- Ton exercice nécessite des connaissances hors-programme de TC (barycentre), mais en tous cas je vous propose ma réponse:
Ma réponse pour problème 33:
- Spoiler:
Et je n'ai pas de problèmes à vous proposer...
bravo ! tu es arrivé à la réponse facilement  j'ai fait AB=5 parce que j'ai supprimé une partie de la question qui dit de construire A et B et les ensembles des points E et F et G | |
|
| | |
maths-au-feminin
Maître
Nombre de messages : 70
Age : 29
Date d'inscription : 07/12/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 17:58 | |
| voila un nouveau probleme
probleme 34
resous dans IR^2 l'equation 2V(x-1)+4V(y-4)=x+y | |
|
| | |
steve 94
Féru
Nombre de messages : 60
Age : 31
Localisation : RABAT
Date d'inscription : 18/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 18:15 | |
| problem 35
https://i.servimg.com/u/f42/16/62/75/03/codeco17.gif | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 18:26 | |
| - steve 94 a écrit:
- problem 35
https://i.servimg.com/u/f42/16/62/75/03/codeco17.gif Il faut respecter les règles (même si le problème 34 est très facile) En plus, tu as mal rédigé le problème 35, voilà un lien dan lequel tu trouvera une réponse https://mathsmaroc.jeun.fr/t17790-olympiadeBonne découverte. | |
|
| | |
steve 94
Féru
Nombre de messages : 60
Age : 31
Localisation : RABAT
Date d'inscription : 18/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Jeu 30 Juin 2011, 18:30 | |
| umm c'est pas la même source !!! | |
|
| | |
upsilon
Maître
Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Ven 01 Juil 2011, 18:27 | |
| Ma solution au problème 34- Spoiler:
2V(x-1)+4V(y-4)=x+y
Donc x+y-2V(x-1)-4V(y-4)=0
Donc x-1+y-4-2V(x-1)-4V(y-4)+5=0
Donc [V(x-1)]²-2V(x-1)+1 +[V(y-4)]²-4V(y-4)+4=0
Donc [V(x-1)-1]²+[V(y-4)-2]²=0
C'est impossible!!(Si [V(x-1)-1]² et [V(y-4)-2]² sont différents de 0)
Autre cas :
V(x-1)-1=0 et V(y-4)-2=0
Donc V(x-1)=1 et V(y-4)=2
Ainsi x-1=1 et y-4=4
Donc x=2et y=8
| |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 20:26 | |
| Puisque personne ne veut proposer, j'interviens avec cet exercice de géométrie:
Problème 35:
Soit ABCD et CDEF deux quadrilatères inscriptibles.
Démontrez que si les droites (AB), (CD) et (EF) sont concourantes, alors le quadrilatère ABFE est inscriptible.
Bonne chance.
Dernière édition par nmo le Lun 04 Juil 2011, 12:17, édité 1 fois | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 21:15 | |
| - nmo a écrit:
- Puisque personne ne veut proposer, j'interviens avec cet exercice de géométrie:
Problème 35:
Soit ABCD et CDEF deux quadrilatères inscriptibles.
Démontrez que si les droites (AB), (CD) et (EF) sont concourantes, alors le quadrilatère ABEF est inscriptible.
Bonne chance. C'est plutôt ABFE ? - Spoiler:
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 22:05 | |
| Ma réponse pour problème 36:- Spoiler:
Soit X l'intersection de (AB), (CD) et (EF). On a ABCD est inscriptible donc  . Et on a  . On conclut que les triangles DXB et AXC sont semblables d'où :  (1) On a CDEF est inscriptible donc  . Et on a  . On conclut que les triangles XCE et XFD sont semblables d'où :  (2) De (1) et (2) on déduit que:  Et on a  . On conclut que les triangles XBE et XFA sont semblables d'où :  (*) Et on a  et  . De (*) on conclut que:  le quadrilatère ABFE est inscriptible.
| |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 22:10 | |
| J'attends vos remarques et observations ... | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 22:20 | |
| En attente de la confirmation de nmo, je vous propose cette équation (très facile). Problème 37:Résoudre dans 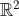 l'équation suivante : ^{2}(xy-2)^{2}+\sqrt{y^{2}-x^{2}}=0) | |
|
| | |
Mehdi.O
Expert sup
Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 22:36 | |
| - ali-mes a écrit:
- nmo a écrit:
- Puisque personne ne veut proposer, j'interviens avec cet exercice de géométrie:
Problème 35:
Soit ABCD et CDEF deux quadrilatères inscriptibles.
Démontrez que si les droites (AB), (CD) et (EF) sont concourantes, alors le quadrilatère ABEF est inscriptible.
Bonne chance.
C'est plutôt ABFE ?
- Spoiler:
C'est une application directe du théorème des axes radicaux  | |
|
| | |
mtb
Féru
Nombre de messages : 30
Age : 29
Date d'inscription : 28/06/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 23:02 | |
| wé facile
on a (x²+y²-4)²(xy-2)²>=0 et racine de (y²-x²)>=0 et bien sur y²>=x² donc valeur absolue de y>=valeur absolue de x et l'equation est (x²+y²-4)²(xy-2)²+racine de y²-x²=0
donc valeur absolue de y =valeur absolue de x et x²=y² donc (2x²-4)²(x²-2)²=0
donc 4(x²-2)ouss4=0 donc x=racine de2 ou x=-racine de2
et y=racine de 2 ou y=-racine de 2 | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Dim 03 Juil 2011, 23:08 | |
| - ali-mes a écrit:
- En attente de la confirmation de nmo, je vous propose cette équation (très facile).
Problème 37:
Résoudre dans 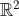l'équation suivante :
solution: (x^2+y^2-4)^2(xy-2)^2+v(y^2-x^2)=0 Donc (x^2+y^2-4)(xy-2)=0 et y^2-x^2=0 Alors x^2+y^2-4=0 et y^2-x^2=0 ou xy-2=0 et y^2-x^2=0 S={(√2 ; √2) ; (-√2 ; √2) ; (√2 ; -√2) ; (-√2 ; -√2) } | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 00:38 | |
| - Mehdi.O a écrit:
- ali-mes a écrit:
- nmo a écrit:
- Puisque personne ne veut proposer, j'interviens avec cet exercice de géométrie:
Problème 35:
Soit ABCD et CDEF deux quadrilatères inscriptibles.
Démontrez que si les droites (AB), (CD) et (EF) sont concourantes, alors le quadrilatère ABEF est inscriptible.
Bonne chance.
C'est plutôt ABFE ?
- Spoiler:
C'est une application directe du théorème des axes radicaux Est ce que ma réponse est juste ? | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 00:40 | |
| - mtb a écrit:
- wé facile
on a (x²+y²-4)²(xy-2)²>=0 et racine de (y²-x²)>=0 et bien sur y²>=x² donc valeur absolue de y>=valeur absolue de x et l'equation est (x²+y²-4)²(xy-2)²+racine de y²-x²=0
donc valeur absolue de y =valeur absolue de x et x²=y² donc (2x²-4)²(x²-2)²=0
donc 4(x²-2)ouss4=0 donc x=racine de2 ou x=-racine de2
et y=racine de 2 ou y=-racine de 2 Postes un nouveau exo, si tu veux ! | |
|
| | |
ali-mes
Expert sup
Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
| |
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 00:44 | |
| | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 00:55 | |
| Problème 38:Soit ABC un triangle . Prouver que : 
Dernière édition par expert_run le Lun 04 Juil 2011, 13:41, édité 2 fois | |
|
| | |
nmo
Expert sup
Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 12:27 | |
| - ali-mes a écrit:
- nmo a écrit:
- Puisque personne ne veut proposer, j'interviens avec cet exercice de géométrie:
Problème 35:
Soit ABCD et CDEF deux quadrilatères inscriptibles.
Démontrez que si les droites (AB), (CD) et (EF) sont concourantes, alors le quadrilatère ABEF est inscriptible.
Bonne chance. C'est plutôt ABFE ? Effectivement. - ali-mes a écrit:
- J'attends vos remarques et observations ...
J'ai lu ta solution, elle est bonne. - expert_run a écrit:
- Soit ABC un triangle . Prouver que :
Il s'agit du problème 38, il faut respecter les règles du jeu.
Dernière édition par nmo le Lun 04 Juil 2011, 18:22, édité 1 fois | |
|
| | |
expert_run
Expert sup
Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Lun 04 Juil 2011, 13:37 | |
| | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> | |
| |
|
| | |
| | << Grand Jeu d'été 2011 de TC ->1ére >> | |
|
