| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
+20n.naoufal sadaso maths-au-feminin Hamouda geom Azerty1995 yasserito helloall Mehdi.A Mehdi.O Meded l'intellectuelle yasmine boubou math konica Nayssi az360 expert_run upsilon ali-mes 24 participants |
|
| Auteur | Message |
|---|
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Jeu 07 Juil 2011, 12:07 Jeu 07 Juil 2011, 12:07 | |
| Solution au problème 40:
angle{AME}=180-angle{ABE}=angle{ABE'}=angle{AM'E'}.
angle{AEM}=angle{ABM}=180-angle{ABM'}=angle{AE'M}.
Donc AEM et AE'M' sont semblables. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Jeu 07 Juil 2011, 12:46 Jeu 07 Juil 2011, 12:46 | |
| oui bravo . tu posté un exe...  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 22:30 Ven 08 Juil 2011, 22:30 | |
| Je vous propose ces 2 exos: Problème 41:Soit ABC un triangle, on construit à l'éxtérieur de ce triangle les carrés  . Notons: \cap%20(CE)) . Montrer que les droites (AP), (A'C) et (A''B) sont concurrents. problème 42:Résoudre dans Z² l'équation: 3x+6y=18.
Dernière édition par ali-mes le Ven 08 Juil 2011, 22:34, édité 1 fois | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 22:31 Ven 08 Juil 2011, 22:31 | |
| Vous pouvez arreter avec la géo!!  J'aime vrmt pas!! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 22:36 Ven 08 Juil 2011, 22:36 | |
| - Nayssi a écrit:
- Vous pouvez arreter avec la géo!!

J'aime vrmt pas!! J'ai proposé l'exo 42, mais croyez moi si vous travaillé dès maintenant de la géométrie, vous allez pas trouvé des difficultés (d'après l'expérience de plusieurs candidats des olympiades), faut bosser la géométrie dès maintenant pour être à la hauteur... | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 22:48 Ven 08 Juil 2011, 22:48 | |
| Solution au problème 42- Spoiler:
On a :3x+6y=18
Soit : x+2y=6
Soit : x+2y=2*1+2*2
Ainsi 1*(x-2)=2*(2-y)
Et comme 1 et 2 premiers entre eux,
Alors : x-2=2k et 2-y=1*k
x=2k+2 et y=2-k avec k de Z
D'où : S={k£ Z/2k+2;2-k)
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 22:54 Ven 08 Juil 2011, 22:54 | |
| Tu peux proposer maintenant un nouveau exo. | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Ven 08 Juil 2011, 23:01 Ven 08 Juil 2011, 23:01 | |
| Problème 43
Résoudre dans IN
ab+bc+ca=2(a+b+c) | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 18:17 Sam 09 Juil 2011, 18:17 | |
| J'ai pas voulut présenter ma réponse hier, mais en tous cas je vais répondre maintenant: Ma réponse pour problème 43:- Spoiler:
On résous dans IN^3 l'équation: ab+ac+bc=2(a+b+c)
Par symétrie de rôles, on peut supposer que: c=<b=<a.
* si c=0, l'équation devient: ab=2(a+b) <=> ab-2a-2b=0 <=> a(b-2)-2b=0
<=> a(b-2)-(2b-4)=4 <=> a(b-2)-2(b-2)=4 <=> (a-2)(b-2)=4
On a: b=<a <=> b-2=<a-2 d'où (a-2=2 et b-2=2) ou (a-2=4 et b-2=1)
<=>(a=4 et b=4) ou (a=6 et b=3)
* si b=c=0, l'équation devient 2a=0 <=> a=0.
* Maintenant supposons que: 1=<c=<b=<a:
l'équation est équivalente à:
ab+ac+bc-2a-2b-2c=0
<=>(ab-a-b)+(ac-a-c)+(bc-b-c)=0
<=>(a(b-1)-b)+(a(c-1)-c)+(b(c-1)-c)=0
<=>(a(b-1)-b)+(a(c-1)-c)+(b(c-1)-c)+3=3
<=>(a(b-1)-b+1)+(a(c-1)-c+1)+(b(c-1)-c+1)=3
<=>(a(b-1)-(b-1))+(a(c-1)-(c-1))+(b(c-1)-(c-1))=3
<=>(a-1)(b-1)+(a-1)(c-1)+(b-1)(c-1)=3
Avec la condition de: 1=<c=<b=<a, on obtient: 0=<(b-1)(c-1)=<(a-1)(c-1)=<(a-1)(b-1)
Ainsi on a :
*3=0+0+3 => (a-1)(b-1)=3 et (a-1)(c-1)=0 et (b-1)(c-1)=0 => (a-1)(b-1)=3 et a=1 et c=1 et b=1=>Absurde (on remplace a=1 et b=1 dans (a-1)(b-1)=3 et on trouve la contradiction).
*3=0+1+2 => (a-1)(b-1)=2 et (a-1)(c-1)=1 et (b-1)(c-1)=0 =>(a-1)(b-1)=2 et (a-1)(c-1)=1 et b=1 et c=1 => Absurde (on remplace b=1 et c=1 dans (a-1)(b-1)=2 et (a-1)(c-1)=1 et on trouve la contradiction).
*3=1+1+1 => (a-1)(b-1)=1 et (a-1)(c-1)=1 et (b-1)(c-1)=1 => a-1=1 et b-1=1 et a-1=1 et c-1=1 et b-1=1 et c-1=1 => a=2 et b=2 et c=2
Synthèse:
Par conséquent: S={(4,4,0)/(0,4,4)/(4,0,4)/(6,3,0)/(3,6,0)/(0,6,3)/(0,3,6)/(3,0,6)/(6,0,3)/(2,2,2)}
A vous de me signaler si vous voyez une faute. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 | |
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 19:28 Sam 09 Juil 2011, 19:28 | |
| Solution au problème 41:
Soit R la rotation de centre A et d'angle 90°, nous R_a(A")=C et R_a(B)=A' ainsi A'C est perpendiculaire à A"B.
Maintenant Soit F l'intersection de ces deux droites, nous avons angle{BPC}=90 et ainsi le quadrilatère BFCP est inscriptible ainsi angle{PFC}=45°. De même nous avons angle{A"FC}=angle{A"AC}=90° ainsi le quadrilatère A'AFC est inscriptible et ainsi angle{AFA"}=45° et ainsi les points A,F et P sont collinéaires, d'où la conclusion. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 19:33 Sam 09 Juil 2011, 19:33 | |
| pourquoi angle{PFC} = 45° !!!! et angle{AFA"}=45° !!! et merci  | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 19:35 Sam 09 Juil 2011, 19:35 | |
| - az360 a écrit:
- pourquoi angle{PFC} = 45° !!!! et angle{AFA"}=45° !!!
et merci  Parce que les deux quadrilatères BFCP et A'AFC sont inscriptibles, je l'ai mentionné | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 19:54 Sam 09 Juil 2011, 19:54 | |
| - Mehdi.O a écrit:
- Solution au problème 41:
Soit R la rotation de centre A et d'angle 90°, nous R_a(A")=C et R_a(B)=A' ainsi A'C est perpendiculaire à A"B.
Maintenant Soit F l'intersection de ces deux droites, nous avons angle{BPC}=90 et ainsi le quadrilatère BFCP est inscriptible ainsi angle{PFC}=45°. De même nous avons angle{A"FC}=angle{A"AC}=90° ainsi le quadrilatère A'AFC est inscriptible et ainsi angle{AFA"}=45° et ainsi les points A,F et P sont collinéaires, d'où la conclusion. Bien, il y a une autre méthode avec Ceva, mais la tienne est plus élégante. A toi le prochain exo. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:06 Sam 09 Juil 2011, 20:06 | |
| Je n'ai pas de problème à proposer je vous laisse la main. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:19 Sam 09 Juil 2011, 20:19 | |
| Ok, je vous propose ces 2 exos:
Problème 44:
Le nombre d'habitants d'un quartier est 160 habitants, Aucun habitant ne dépasse 78 ans. Montrer qu'l existe au moins trois habitants ayant le même age.
Problème 45:
Soit ABC un triangle dont tous les angles sont aigus, et soit H l'otrthocentre de ABC.
Considérons E, F et G les projections orthogonales de A, B et C sur [BC], [AC] et [AB].
Montrer que H est le centre du cercle inscrit au triangle EFG. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:29 Sam 09 Juil 2011, 20:29 | |
| Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:32 Sam 09 Juil 2011, 20:32 | |
| Solution du problème 44:
D'après la version généralisée du principe des tiroirs on a au moins -E(-160/78)=3 habitants ayant le même age.
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:45 Sam 09 Juil 2011, 20:45 | |
| je crois que Mehdi.O ne veut pas proposer un autre exo...
Donc, expert-run poste un nouveau exo. | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:47 Sam 09 Juil 2011, 20:47 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:50 Sam 09 Juil 2011, 20:50 | |
| - Mehdi.O a écrit:
- Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG Les points A, H et E sont collinéaires ... En plus, c'est quoi D ? Je crois que tu as travaillé avec d'autres points, à toi de rectifier... | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:59 Sam 09 Juil 2011, 20:59 | |
| Problème 46: Montrer que l'ensemble des réels x qui vérifient l'inéquation 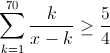 et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 20:59 Sam 09 Juil 2011, 20:59 | |
| - ali-mes a écrit:
- Mehdi.O a écrit:
- Solution au problème 44:
Application directe du principe des tiroirs, vu que 2*78<160.
Solution au problème 45:
Remarquer que les deux quadrilatères AFHE et EHDC sont inscriptibles: ainsi : angle{FEH}=angle{FAH}=angle{BAD}=90-angle{ABC}=angle{HCD}=angle{HED}, aini [EH) est bissectrice de l'angle <FEG et de même on prouve les autres biisectrices, ainsi H est le centre du cercle inscrit de EFG
Les points A, H et E sont collinéaires ... En plus, c'est quoi D ?
Je crois que tu as travaillé avec d'autres points, à toi de rectifier... Oui désolé, voici les points avec lesquelles j'ai travailél, H orthocentre, D P.O de A sur BC, E sur AC et F sur AB. Amicalement. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 21:04 Sam 09 Juil 2011, 21:04 | |
| - expert_run a écrit:
- Problème 46:
Montrer que l'ensemble des réels x qui vérifient l'inéquation 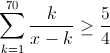 et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. Cela veut-il dire que si on a une intervalle [a,b] sa longueur est b-a ?! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  Sam 09 Juil 2011, 21:06 Sam 09 Juil 2011, 21:06 | |
| - Mehdi.O a écrit:
- expert_run a écrit:
- Problème 46:
Montrer que l'ensemble des réels x qui vérifient l'inéquation 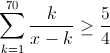 et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. et la réunion d'intervalles disjoints dont la somme des longueurs a pour valeur 1988. Cela veut-il dire que si on a une intervalle [a,b] sa longueur est b-a ?! oui c'est ça. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >> Sujet: Re: << Grand Jeu d'été 2011 de TC ->1ére >>  | |
| |
|
  | |
| | << Grand Jeu d'été 2011 de TC ->1ére >> |  |
|
