| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 09 Jan 2014, 16:43 Jeu 09 Jan 2014, 16:43 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 09 Jan 2014, 17:01 Jeu 09 Jan 2014, 17:01 | |
| Montrer que : 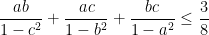 avec a,b,c>0 et a+b+c=1 | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 16:00 Mar 14 Jan 2014, 16:00 | |
|  Mais, avec a=x² ... :  Donc :  Et puisque la fonction x-> x/(x+1) est concave sur IR+ nous avons par Jensen :  . QED . J'aimerais bien, si possible voir ta solution Ahmed Taha. Pour voir seulement s'il y a une solution plus élégante. Merci | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:05 Mar 14 Jan 2014, 17:05 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:08 Mar 14 Jan 2014, 17:08 | |
| Merci pour le livre, intéressant. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 14 Jan 2014, 17:27 Mar 14 Jan 2014, 17:27 | |
| - Humber a écrit:
- Merci pour le livre, intéressant.
c rien  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 16 Jan 2014, 18:16 Jeu 16 Jan 2014, 18:16 | |
| | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 18 Jan 2014, 23:28 Sam 18 Jan 2014, 23:28 | |
| L'inégalité est équivalente à prouver que : ab+bc+ac+abc≥4 ou encore (a-1)(b-1)(1-c)+a+b+c+2abc≥5 Observons que a,b,c ne peuvent être tous supérieurs ou inférieurs à 1. Supposons donc SPDG que (a,b)≥1 et que 1≥c. Nous avons donc (a-1)(b-1)≥0 et donc (a-1)(b-1)(1-c)+a+b+c+2abc≥a+b+c+2abc Il suffit ainsi de prouver que a+b+c+2abc≥5Si abc≥1 l'inégalité est claire parce que a+b+c≥3 . Si 1≥abc : <==>  Prenons la fonction f: x->p/x+2x avec p²=(ab+bc+ac)²≥3abc(a+b+c)=3(ab+bc+ac) ==> p≥3 et x=abc 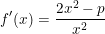 1≥x ==>2x²-p <0 donc f est décroissante sur ]0,1], ainsi f(x)≤f(1) <==> f(x)≥p+2≥5 Donc p/x+2x=(ab+bc+ac)/abc+2abc≥5 ==>a+b+c+2abc≥5. CQFD Finalement je pense que le cas 1≥abc est inutile vu que lorsque(a,b)≥1 et c en est inférieure, abc est systématiquement supérieur ou égal à 1 . Reste à le démontrer. | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 19 Jan 2014, 03:21 Dim 19 Jan 2014, 03:21 | |
| n≥2 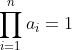 Prouver que : | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 25 Jan 2014, 19:42 Sam 25 Jan 2014, 19:42 | |
| Pour le problème de M. Ahmed TAHA du 9 Janvier 2014, j'ai trouvé une solution dans laquelle on n'utilise que les IAG. Soient a,b et c des réels positifs tel que a+b+c=1. Montrer que ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . On a ab/(1-c^2 )= ab/(〖(a+b+c)〗^2-c^2 )=ab/(a^2+b^2+2ab+2bc+2ca) . On a aussi a^2+b^2+2ab+2bc+2ca≥8〖(a^6 b^6 c^4)〗^(1/  =8a^(3/4) b^(3/4) c^(1/2) ∶IAG . ↔1/(8a^(3/4) b^(3/4) c^(1/2) )≥1/(a^2+b^2+2ab+2bc+2ca) ↔(a^(1/4) b^(1/4))/(8c^(1/2) )≥ab/(a^2+b^2+2ab+2bc+2ca) donc ab/(1-c^2 )≤(a^(1/4) b^(1/4))/(8c^(1/2) ) ,de même on a bc/(1-a^2 )≤(b^(1/4) c^(1/4))/(8a^(1/2) ) et ca/(1-b^2 )≤(c^(1/4) a^(1/4))/(8b^(1/2) ) , donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤1/8 ((a^(1/4) b^(1/4))/(8c^(1/2) )+(b^(1/4) c^(1/4))/(8a^(1/2) )+(c^(1/4) a^(1/4))/(8b^(1/2) )) ≤1/8*3〖((a^(1/4) b^(1/4))/(8c^(1/2) )*(b^(1/4) c^(1/4))/(8a^(1/2) )*(c^(1/4) a^(1/4))/(8b^(1/2) ))〗^(1/3)=3/8 ∶IAG , donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 13:58 Mer 29 Jan 2014, 13:58 | |
| - aymanemaysae a écrit:
- Pour le problème de M. Ahmed TAHA du 9 Janvier 2014, j'ai trouvé une solution dans laquelle on n'utilise que les IAG.
Soient a,b et c des réels positifs tel que a+b+c=1. Montrer que ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 .
On a ab/(1-c^2 )= ab/(〖(a+b+c)〗^2-c^2 )=ab/(a^2+b^2+2ab+2bc+2ca) .
On a aussi a^2+b^2+2ab+2bc+2ca≥8〖(a^6 b^6 c^4)〗^(1/ =8a^(3/4) b^(3/4) c^(1/2) ∶IAG . =8a^(3/4) b^(3/4) c^(1/2) ∶IAG .
↔1/(8a^(3/4) b^(3/4) c^(1/2) )≥1/(a^2+b^2+2ab+2bc+2ca) ↔(a^(1/4) b^(1/4))/(8c^(1/2) )≥ab/(a^2+b^2+2ab+2bc+2ca)
donc ab/(1-c^2 )≤(a^(1/4) b^(1/4))/(8c^(1/2) ) ,de même on a bc/(1-a^2 )≤(b^(1/4) c^(1/4))/(8a^(1/2) ) et ca/(1-b^2 )≤(c^(1/4) a^(1/4))/(8b^(1/2) ) ,
donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤1/8 ((a^(1/4) b^(1/4))/(8c^(1/2) )+(b^(1/4) c^(1/4))/(8a^(1/2) )+(c^(1/4) a^(1/4))/(8b^(1/2) )) ≤1/8*3〖((a^(1/4) b^(1/4))/(8c^(1/2) )*(b^(1/4) c^(1/4))/(8a^(1/2) )*(c^(1/4) a^(1/4))/(8b^(1/2) ))〗^(1/3)=3/8 ∶IAG ,
donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . Bonsoir Aymanemaysae, (a b)^(1/4)/sqrt(c)+(c b)^(1/4)/sqrt(a)+(a c)^(1/4)/sqrt(b) ≥ 3 malheureusement | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 14:45 Mer 29 Jan 2014, 14:45 | |
| Bon, je change de problème pour ne pas laisser le marathon ainsi: En voici un facile : Problème alternatif :Prouver que :  Pour tous réels a,b,c . | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 18:54 Mer 29 Jan 2014, 18:54 | |
| Tout d'abord, On a: |x|+|y|>|x+y| pour tous x;y de R², donc |x|+|1-x|>1 pour tout x. On a par caushy schwarz:  | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 19:03 Mer 29 Jan 2014, 19:03 | |
| Soit a,b et c des réels positifs. Prouvez que:  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 | |
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 19:41 Mer 29 Jan 2014, 19:41 | |
| Soit a,b et c des réels positifs tel que : ab+ab+bc+2abc=1 Montrer que : 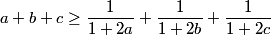 | |
|
  | |
Amine Natik
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 28
Date d'inscription : 26/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 22:56 Mer 29 Jan 2014, 22:56 | |
| Il suffit de poser Cyc(a=x/(y+z) ) . et puis on remplace : Il s'agit de prouver que :
/Sum(x/(y+z)) >= /Sum( (y+z)/(y+z+2x) ) . puisque l'inégalité est homogène on peut supposer x+y+z=1. donc :
<=> /sum( x/(1-x) ) >= / Sum( (1-x)/(1+x) )
<=> /Sum( (3x-1)/(1-x²) ) >=0.
et c'est une conséquence de Jensen car la fonction f(x)=(3x-1)/(1-x²) est convexe sur [0,1] .
CQFD | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 29 Jan 2014, 23:37 Mer 29 Jan 2014, 23:37 | |
| La" fameuse "substitution fait l'affaire. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 30 Jan 2014, 09:56 Jeu 30 Jan 2014, 09:56 | |
| Suite à la remarque de M. Humber, que je remercie amplement, remarque du 29 Janvier 2014 à ma propos de ma proposition pour la résolution du problème de M. Ahmed TAHA du 9 Janvier 2014, je tiens à préciser que la méthode reste valable, malgré une erreur de frappe que j'ai commise: quand j'ai mis le (1/huit) en facteur dans le RHS de l'inéquation, j'ai laissé traîner le (huit) au dénominateur.
En demandant votre pardon pour cette inadvertance, je corrige le dernier paragraphe de ma solution:
donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤1/8 ((a^(1/4) b^(1/4))/(c^(1/2) )+(b^(1/4) c^(1/4))/(a^(1/2) )+(c^(1/4) a^(1/4))/(b^(1/2) )) ≤1/8*3〖((a^(1/4) b^(1/4))/(c^(1/2) )*(b^(1/4) c^(1/4))/(a^(1/2) )*(c^(1/4) a^(1/4))/(b^(1/2) ))〗^(1/3)=3/8 ∶IAG ,
donc ab/(1-c^2 )+bc/(1-a^2 )+ca/(1-b^2 )≤ 3/8 . | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 30 Jan 2014, 12:15 Jeu 30 Jan 2014, 12:15 | |
| Soit a,b et c des réels positifs tel que : ab+bc+ca+2abc=1 Montrer que : 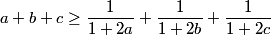 Je me suis permis de rectifier l'énoncé du sujet: j'ai mis ab+bc+ca+2abc=1 à la place de ab+ab+bc+2abc=1. J'ai présumé que ce n'était qu'une faute de frappe. On a 1/(1+2a) + 1/(1+2b) + 1/(1+2c) = (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+4(ab+bc+ca+2abc)+1) = (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+5) : car ab+bc+ca+2abc=1, donc 1/(1+2a) + 1/(1+2b) + 1/(1+2c) < a+b+c <--> (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+5) < a+b+c <--> (4(a+b+c)+4(ab+bc+ca)+3) < 2(a+b+c)^2 + 5(a+b+c) <--> 4(ab+bc+ca) < 2(a^2+b^2+c^2 + 2ab+2bc+2ca)+(a+b+c) <--> 0 < 2(a^2+b^2+c^2)+(a+b+c) : expression logiquement vraie car a,b et c sont des réels positifs, donc 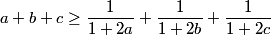 est aussi vraie sous les conditions du problème. Je me permets aussi de me demander si le changement de variables opéré dans l'autre solution proposée, vérifie la condition ab+bc+ca+2abc=1. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 30 Jan 2014, 18:12 Jeu 30 Jan 2014, 18:12 | |
| - aymanemaysae a écrit:
- Soit a,b et c des réels positifs tel que : ab+bc+ca+2abc=1
Montrer que :
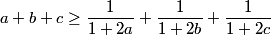
Je me suis permis de rectifier l'énoncé du sujet: j'ai mis ab+bc+ca+2abc=1 à la place de ab+ab+bc+2abc=1. J'ai présumé que ce n'était qu'une faute de frappe.
On a 1/(1+2a) + 1/(1+2b) + 1/(1+2c)
= (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+4(ab+bc+ca+2abc)+1)
= (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+5) : car ab+bc+ca+2abc=1,
donc 1/(1+2a) + 1/(1+2b) + 1/(1+2c) < a+b+c
<--> (4(a+b+c)+4(ab+bc+ca)+3)/(2(a+b+c)+5) < a+b+c
<--> (4(a+b+c)+4(ab+bc+ca)+3) < 2(a+b+c)^2 + 5(a+b+c)
<-->4(ab+bc+ca) < 2(a^2+b^2+c^2 + 2ab+2bc+2ca)+(a+b+c)
<--> 0 < 2(a^2+b^2+c^2)+(a+b+c) : expression logiquement vraie car a,b et c sont des réels positifs, donc
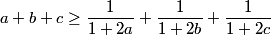
est aussi vraie sous les conditions du problème.
Je me permets aussi de me demander si le changement de variables opéré dans l'autre solution proposée, vérifie la condition ab+bc+ca+2abc=1. non c faut mr aymanemaysae car on a le cas d'égalité si a=b=c=1/2 l'inégalité équivalente a : 2(x+y+z)^2+(x+y+z) > 3+4(xy+xz+yz) | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Jeu 30 Jan 2014, 20:55 Jeu 30 Jan 2014, 20:55 | |
| voici une autre
Soit x,y et z des réels positifs tel que : x+y+z=3
Montrer que : 3(xy+xz+yz)²+xyz(xy+xz+yz)>10xyz
et que : 9(xy+xz+yz)+4xyz(xy+xz+yz)>4(xy+xz+yz)²+3xyz | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 01 Fév 2014, 21:24 Sam 01 Fév 2014, 21:24 | |
| Merci M. Ahmed TAHA pour la remarque: j'ai oublié de prendre en compte le (3) dans mon passage de la ligne : <--> (4(a+b+c)+4(ab+bc+ca)+3) < 2(a+b+c)^2 + 5(a+b+c)
à la ligne : <--> 4(ab+bc+ca) < 2(a^2+b^2+c^2 + 2ab+2bc+2ca)+(a+b+c)
ce qui a fait chavirer mon bâteau et jeter ma démonstration à l'eau.
Je vous suis très reconnaissant. | |
|
  | |
Nas8
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 28
Date d'inscription : 26/11/2011
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Fév 2014, 15:09 Dim 02 Fév 2014, 15:09 | |
| Soit x,y et z des réels positifs tel que : x+y+z=3
Montrer que : (E) 3(xy+xz+yz)²+xyz(xy+xz+yz)>10xyz
(E) (x+y+z)(1/x + 1/y + 1/z)(xy+yz+yz) + (xy+yz+yz) > 10
10(xy+yz+yz) > 10 ==> (xy+yz+xz) > 1 ce qui doit etre correct | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 02 Fév 2014, 15:40 Dim 02 Fév 2014, 15:40 | |
| - aymanemaysae a écrit:
- Merci M. Ahmed TAHA pour la remarque: j'ai oublié de prendre en compte le (3) dans mon passage de la ligne : <--> (4(a+b+c)+4(ab+bc+ca)+3) < 2(a+b+c)^2 + 5(a+b+c)
à la ligne : <--> 4(ab+bc+ca) < 2(a^2+b^2+c^2 + 2ab+2bc+2ca)+(a+b+c)
ce qui a fait chavirer mon bâteau et jeter ma démonstration à l'eau.
Je vous suis très reconnaissant. ahlan mr aymanemaysae kan 3lik tkemel lborhan o ghatl9a blli dik l'inégalité sahla voir ce lien http://www.artofproblemsolving.com/Forum/viewtopic.php?f=51&t=573326&p=3375908#p3375908 j'ai déja fait la même démonstration
Dernière édition par Ahmed Taha le Dim 02 Fév 2014, 15:45, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
