| | Grand Jeu d'Hiver TSM 2007-2008 |  |
|
+37Sasuke yassine-mansouri Weierstrass raito321 $arah Laalej *pilote militaire * R.kira abdellatif90 Fourrier-D.Blaine clever007 hamzaaa JASPER saiif3301 kalm mouadpimp fermat1988 Nea® sweet_girl coucou namily adam o0aminbe0o codex00 prof rockabdel callo wiles ali 20/20 lonly omis otman4u badr mohamed_01_01 Conan stof065 Alaoui.Omar 41 participants |
|
| Auteur | Message |
|---|
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 07:19 Sam 29 Sep 2007, 07:19 | |
|
- Être Inscrit(éléves Du TSM)
- Être sérieux ,On est là Pour étudié!
-Écrire le Numéro d'exercice proposé et le livre et Tout L'énoncer .
-Essayé De Poster Tout Les exercice du Livre Soit Assez Facile Ou difficile!
- Ne pas utiliser le langage SMS .
- Jamais de hors sujet .
- Essayez si c'est possible d'écrire vos réponses à l'aide de latex ou de maths-type ou le autre logiciel de maths .(Pour MATHTYPE ICI)
- Ne trichez pas .
- Tous les exos concernant le programme TSM .
-Les réponses doivent posté ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
-chaque réponse Lisible , correcte et Complète Vaut 2 points.
En cas de retard ou Triche .. le participant aura -2points.
-Pour Obtenir Une étoile  il Faut Avoir 20 Points. il Faut Avoir 20 Points.
-Pour l'aide Consulter le groupe organisateurs :Alaoui.Omar,Stof065 par mp ou émail Pas ICI.
 Liste des participant: Liste des participant:Samrota Alaoui.omar Badr Wiles Conan Coucou Omis o0aminbe0o ali 20/20 baku mohamed_01_01 surferrip callo stof065 otman4u JASPER codex00 ali_tox rockabdel prof kalm reda031-245 galoiscauchey youf105 safa Nea  namily saiif3301 clever007 yassine-mansouri abdellatif90 *pilote militaire * $arah Liste des Observateurs :Mr.PAtrick (pco)

Dernière édition par le Mar 29 Jan 2008, 22:54, édité 15 fois | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 08:26 Sam 29 Sep 2007, 08:26 | |
| EX N°:1 ( Demonstration du propriété 3.3 page 19 du livre almoufid) Soit f Une fonction admis une limite a x_0 tel que:  Demontrer en utilisant la definition topographique du limite que : 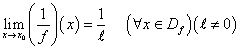 Pour l'aide Consulter le groupe organisateurs :Alaoui.Omar,Stof065 par mp ou email Pas ICI.
| |
|
  | |
stof065
Expert sup

 Nombre de messages : 540 Nombre de messages : 540
Age : 34
Date d'inscription : 01/02/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 11:49 Sam 29 Sep 2007, 11:49 | |
| trés bonne exo  départ exceptionnel  | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 12:02 Sam 29 Sep 2007, 12:02 | |
| je pose : A = quelque soit . et I I = valeur absolue soit e=epsilon > 0 on veux arriver à : il existe α > 0 tel que pour tout x de Df: Ix-x0I =< α => I 1/f(x) - 1/L I < e on a : limf(x) =L ( L#0) x->x0 donc f admet une valeur minimale m sur l'intervale I (de centre x0) <=> (Ax£I) : m =< f(x) => m =< I f(x) I => m ILI =< I Lf(x) I donc (Ax£I) : 1/ I Lf(x) I =< 1/ m ILIet on a : limf(x) =L ( L#0) x->x0 <=> (Ax£I) il existe α > 0 tel que pour tout x de I : Ix-x0I =< α => I f(x) - L I < e => I (f(x)-L)/(Lf(x) I < e => I 1/f(x) - 1/L I < edonc lim 1/f(x) = 1/L  x->x0 | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 12:19 Sam 29 Sep 2007, 12:19 | |
| Bonne Reponse ,Alors Poste " EX N°:2 " | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 12:26 Sam 29 Sep 2007, 12:26 | |
| EX N°:2 "
c'est l'exercise 71 page 42 du livre almoufid :
soit f une fonction numéique continue sur R tel que :
(Ax£R) : f(x) # x (A = quelque soit )
Montrer que l'équation : fof(x) = x n'admet aucun solution dans R | |
|
  | |
mohamed_01_01
Expert grade1

 Nombre de messages : 465 Nombre de messages : 465
Age : 34
Date d'inscription : 07/09/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 12:42 Sam 29 Sep 2007, 12:42 | |
| f(x) est contenue est defirent en x donc que soit x£R (f(x)>x ou
f(x)<x) si f(x)>x donc f(f(x)>f(x)>x donc f(fx) n'igale pas x pour f(x)<x donc f(f(x)<f(x)<x donc f(f(x) est defirent de x | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 14:13 Sam 29 Sep 2007, 14:13 | |
| | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 14:45 Sam 29 Sep 2007, 14:45 | |
| c juste mohamed_01_01
poste exo N3 | |
|
  | |
mohamed_01_01
Expert grade1

 Nombre de messages : 465 Nombre de messages : 465
Age : 34
Date d'inscription : 07/09/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:09 Sam 29 Sep 2007, 15:09 | |
| | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:12 Sam 29 Sep 2007, 15:12 | |
| - mohamed_01_01 a écrit:
- ex90 page44
rediger le pour qui na pas de livres | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:23 Sam 29 Sep 2007, 15:23 | |
| salut
f(x) est contuni sur [a,b]
=> f[a,b]=[m,M]
alors quelque soit x : m<=f(x)=<M
alors m<=f(x_1)=<M
m<=f(x_2)=<M
m<=f(x_3)=<M
m<=f(x_n)=<M
alor n.m =<f(x1)+f(x_2)+..+f(x_n)=<n.M
d'aprés t.v.i
existe c de [a,b]tels que f(c)=1/n.[f(x1)+f(x_2)+..+f(x_n)]
ps: il ya une faute dans l'exo
f est continue sur [a,b] et pas [0;1] | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:27 Sam 29 Sep 2007, 15:27 | |
| oui , c pour cette faute que je l'ai laisser , alors mohamed tu dois changer l'exo | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:36 Sam 29 Sep 2007, 15:36 | |
| - Alaoui.Omar a écrit:
- EX N°:1 ( Demonstration du propriété 3.3 page 19 du livre almoufid)
Soit f Une fonction admis une limite a x_0 tel que:

Demontrer en utilisant la definition topographique du limite que :
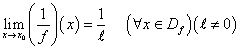
Pour l'aide Consulter le groupe organisateurs :Alaoui.Omar,Stof065 par mp ou email Pas ICI.
mais a si omar la réponse de cette exercice est ecrite sur le livre tu dois donner un autre exo | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:40 Sam 29 Sep 2007, 15:40 | |
| - otman4u a écrit:
- Alaoui.Omar a écrit:
- EX N°:1 ( Demonstration du propriété 3.3 page 19 du livre almoufid)
Soit f Une fonction admis une limite a x_0 tel que:

Demontrer en utilisant la definition topographique du limite que :
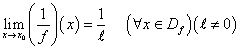
Pour l'aide Consulter le groupe organisateurs :Alaoui.Omar,Stof065 par mp ou email Pas ICI.
mais a si omar
la réponse de cette exercice est ecrite sur le livre
tu dois donner un autre exo oui ta raison | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:40 Sam 29 Sep 2007, 15:40 | |
| | |
|
  | |
mohamed_01_01
Expert grade1

 Nombre de messages : 465 Nombre de messages : 465
Age : 34
Date d'inscription : 07/09/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:45 Sam 29 Sep 2007, 15:45 | |
| oui c'est juste et f est contenue sur [a;b] ;poste l'exerice n4 | |
|
  | |
otman4u
Expert grade2

 Nombre de messages : 349 Nombre de messages : 349
Age : 33
Date d'inscription : 29/04/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:48 Sam 29 Sep 2007, 15:48 | |
| exo n 4
exo 70 p 42
f:[a,b]--->[a,b] et f est contunie sur [a,b]
montrer que f admet un ponit solide(نقطة صامدة) | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:56 Sam 29 Sep 2007, 15:56 | |
| - otman4u a écrit:
- exo n 4
exo 70 p 42
f:[a,b]--->[a,b] et f est contunie sur [a,b]
montrer que f admet un ponit solide(نقطة صامدة) est que le piont solide vaut dire que f est constanre sur le segment a ;b | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:57 Sam 29 Sep 2007, 15:57 | |
| nokta samida ca veut dire existe un c en [a,b] tel ke f(c)=c
poson h(x)=f(x)-x et continue
a<f(a)<b=> 0<f(a)-a
a<f(b)<b => f(b)-b<0
alors h(a).h(b)<0 et pui selon tvi existe un certain c de [a.b] tels ke f(c) =c dou le resulta | |
|
  | |
badr
Expert sup

 Nombre de messages : 1408 Nombre de messages : 1408
Age : 35
Localisation : RIFLAND
Date d'inscription : 10/09/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 15:59 Sam 29 Sep 2007, 15:59 | |
|
Dernière édition par le Sam 29 Sep 2007, 16:02, édité 1 fois | |
|
  | |
mohamed_01_01
Expert grade1

 Nombre de messages : 465 Nombre de messages : 465
Age : 34
Date d'inscription : 07/09/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 16:00 Sam 29 Sep 2007, 16:00 | |
| c'est juste omis donne l'exo n5 | |
|
  | |
omis
Expert grade2

 Nombre de messages : 333 Nombre de messages : 333
Age : 33
Date d'inscription : 25/03/2007
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 16:12 Sam 29 Sep 2007, 16:12 | |
| Exo n:5
exo 89 page 44
f et g deux fonctions definie de [0,1]-->[0,1] et continue sur [0,1]
supposant que fog(x)=gof(x) qqsoit x £ [0,1]
montrez qu'il existe un certain alpha £[0,1] : f(alpha)=g(alpha) | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  Sam 29 Sep 2007, 17:43 Sam 29 Sep 2007, 17:43 | |
| supposons que pour tout x de [0;1] f(x)#g(x) (avec le TVI)
=>
(quelque soit x de [0;1]) f(x)>g(x) ou (quelque soit x de [0;1]) f(x)<g(x)
on prend la fonction h(x) = f(x)-g(x) (quelque soit x de [0;1]) h(x) > 0 ou (quelque soit x de [0;1]) h(x) < 0
h est continue sur [0;1] donc elle admet une valeur minimale m et une valeur maximale M sur [0;1]
<=>
(quelque soit x de [0;1]) h(x) >= m ou (quelque soit x de [0;1]) h(x) =<M
<=> (quelque soit x de [0;1]) f(x)-g(x) >= m *
ou (quelque soit x de [0;1]) f(x) - g(x) =< M **
j'etudie le cas (*) pour le cas (**) c'est une symetrie.
(*) par une simple reccurence on trouve que :
(quelque soit n de N*) (quelque soit x de [0;1]) f[n](x) >= g[n](x)+nm
et on a f[n] et g[n] sont aussi continues sur [0;1] puisque f et g sont continues sur [0;1] vers [0;1].
donc (quelque soit x de [0;1]) -1 =< f[n](x) - g[n](x) =< 1
et on a
(quelque soit n de N*) (quelque soit x de [0;1]) f[n](x) - g[n](x) >= nm
et lim nm = +00 donc lim f[n](x) - g[n](x) = +00
n->+00 n->+00
contradiction
avec le fait que (quelque soit x de [0;1]) -1 =< f[n](x) - g[n](x) =< 1
=> (il existe c de [0;1]) f(c) = g(c) | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 | |
  | |
Contenu sponsorisé
 |  Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008 Sujet: Re: Grand Jeu d'Hiver TSM 2007-2008  | |
| |
|
  | |
| | Grand Jeu d'Hiver TSM 2007-2008 |  |
|
