Grand Jeu d'Hiver TSM 2007-2008

Alaoui.Omar a écrit:

badr a écrit:

oki Omar

soit f une fonction définie sur R et périodique de période T .on suppose qu’il existe un réel `k tel que
limf(x)=k
x-->+00
1. montrer que f est constante de constante ...??!`

De Kél COnstante tu Parle?

f(x)=k qq soit x de R

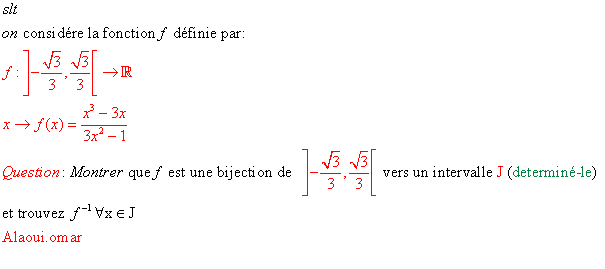P.S 2Jours sont déjà passé Badr!

Est ce que c'est Trés Difficile Cet exo?! C'est Grave Vraiment essayé vous arrivez.

Le fait que
tan(3t)=(3tant-tan^3t)/(1-3tan²t)
résoud cet exo

codex00 a écrit:

Le fait que
tan(3t)=(3tant-tan^3t)/(1-3tan²t)
résoud cet exo

SVP La Reponse COMPTé c'est de A a Z et Pas des idées ,Nous Somme Pas dans le forum d'olympiad!

Désolé, mais j'ai po suffisemment de temps je crois que c'est la même chose pour les autres membres, c'est pour ça qu'ils répondent po (désolé pour cet hors sujet)

codex00 a écrit:

Désolé, mais j'ai po suffisemment de temps je crois que c'est la même chose pour les autres membres, c'est pour ça qu'ils répondent po (désolé pour cet hors sujet)

Ben quand Meme essaye de redigé Une Courte Solution Claire ,COmme ça On continuera Notre Jeu .

Vraiment désolé

En plus il y a un décalage entre les membres ! on est encore en suites suivant le nouveau programme !

coucou a écrit:

En plus il y a un décalage entre les membres ! on est encore en suites suivant le nouveau programme !

Le premier Leçon c'est les limites et continuation Pas Les Suites Dans Le programme

enfin je parle des fonctions réciproques ! je vois que certanis ont dèjà fait ! alors que c'est la 4ème leçon je crois
(oui les suites est la 2eme leçon)

AUtre Exercice:

la deuxieme limite :
lim x[(1+1/x +1/x^3 ) +m ]
+00

1 er cas :
m#-1
a - m supérieur à -1 lim=+00
b- m inférieur à -1 lim=-00

2 eme cas :
m=-1

lim (x²+1)/[(x^3+x²+1)^2/3 + x(x^3+x²+1)^1/3 +x²)]
+00
=1/3


la deuxieme limite:
lim (x^4 +x^3)^1/4 -x
+00
= lim x^3/[(x^4+x^3)^1/4 + x)(( x^4+x^3)^1/2 + x²)]


= 1/4

et arctan est continue en 1/4
donc l=+00

alors ?

Ou est c'est Toute a fait Juste Callo TU peux Poster ton exercice Mnt.
A+

un exo normal :
ex 59 des suites :
P(x)=x^n + x^(n-1)+..............+x-1

1-montrer que P(x)=0 admet une solution unique a_n appartenant à [0,1]
2-montrer que (a_n) est decroissante
3-montrer que 2*a_n = 1+ (a_n)^n+1
4-determiner lim a_n

1) calcule p(0)=-1<0 et p(1)=n-1>0 (n£N*)..
2)on considere Pn(x)=x^n...+x-1..on a Pn+1(x)>Pn(x)
donc Pn+1(a_(n+1))>Pn(a_n+1) donc 0>Pn(a_n+1)=>
Pn(a_n)>Pn(a_n+1) on P'(x)>0 donc a_n>a_n+1(P est contnue sur R)
3)Pn(a_n)=a_n^n....a_n+1-2=((a_n^(n+1)-1)/(a_n-1))-2=0 d'ou la resultat
4) a_n decroisante est masgora donc convergente donc liman=l (0<l<1)
donc lim(2*a_n)=2l=lim(a_n^(n+1)+1)=0+1 donc l=1/2

comment tu t'es permis d'écrire :lim(a_n^(n+1)+1)=0+1 ??
c vrai qu'on a lim q^n=0 si -1<q<1
mais là il sagit d'une suite!!

coucou a écrit:

comment tu t'es permis d'écrire :lim(a_n^(n+1)+1)=0+1 ??
c vrai qu'on a lim q^n=0 si -1<q<1
mais là il sagit d'une suite!!

calculer lim(a_n^(n+1))="l^(+00)"=0 (car 0<l<1)

l'intervalle [0,1] est fermé ( 1 est comprise) donc il faut penser comment l'eliminer. Mais en tt la methode est bonne.

salut oui c'est vrai callo ; et pour elimner cette cas il n'ya qu'à calculer a_2 (on va trouve que a_2^2+a_2-1=0) pn va trv que a_2=c<1 et a_n est decroisante donc que soit n>=2 a_n<c don l<=c<1..donc l#1

voici mon exo:
on considre une suite a_n est converge telque l est sa finie demontrer que lim((a_1+a_2....a_n)/n)=l

dejà posté . voir lemme de cesario ou klk chose comme ça postée par codex aujourd'hui .

ok je vais le changer