Grand Jeu d'Hiver TSM 2007-2008

Conan a écrit:

supposons que pour tout x de [0;1] f(x)#g(x) (avec le TVI)

=>

(quelque soit x de [0;1]) f(x)>g(x) ou (quelque soit x de [0;1]) f(x)<g(x)

on prend la fonction h(x) = f(x)-g(x) (quelque soit x de [0;1]) h(x) > 0 ou (quelque soit x de [0;1]) h(x) < 0

h est continue sur [0;1] donc elle admet une valeur minimale m et une valeur maximale M sur [0;1]

<=>
(quelque soit x de [0;1]) h(x) >= m ou (quelque soit x de [0;1]) h(x) =<M

<=> (quelque soit x de [0;1]) f(x)-g(x) >= m *
ou (quelque soit x de [0;1]) f(x) - g(x) =< M **

j'etudie le cas (*) pour le cas (**) c'est une symetrie.

(*) par une simple reccurence on trouve que :

(quelque soit n de N*) (quelque soit x de [0;1]) f[n](x) >= g[n](x)+nm

et on a f[n] et g[n] sont aussi continues sur [0;1] puisque f et g sont continues sur [0;1] vers [0;1].

donc (quelque soit x de [0;1]) -1 =< f[n](x) - g[n](x) =< 1

et on a
(quelque soit n de N*) (quelque soit x de [0;1]) f[n](x) - g[n](x) >= nm

et lim nm = +00 donc lim f[n](x) - g[n](x) = +00
n->+00 n->+00

contradiction
avec le fait que (quelque soit x de [0;1]) -1 =< f[n](x) - g[n](x) =< 1

=> (il existe c de [0;1]) f(c) = g(c)

waw
tu as juste recopier la methode de dimadima
de A a Z
on veut des methodes originals pour b1 manipuler les lecons

lonly a écrit:

waw
tu as juste recopier la methode de dimadima
de A a Z
on veut des methodes originals pour b1 manipuler les lecons

attention a ce que tu dis lonly , cet exo je l'ai fais il y a pas mal de temps , d'ailleur je n'ai pas copier , mais seulement je connaisser bien la démarche

otman4u a écrit:

Alaoui.Omar a écrit:

EX N°:1 ( Demonstration du propriété 3.3 page 19 du livre almoufid)

Soit f Une fonction admis une limite a x_0 tel que:


Demontrer en utilisant la definition topographique du limite que :

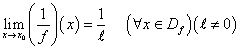
Pour l'aide Consulter le groupe organisateurs :Alaoui.Omar,Stof065 par mp ou email Pas ICI.

mais a si omar
la réponse de cette exercice est ecrite sur le livre
tu dois donner un autre exo

Non , La réponse de cet exo n'est pas ecrite Sur Le livre (tu peux verifier avant de Posté ton message .

voici l'exo N6 (l'exo 72 page 42 almoufid)

soit f une fonction numérique continue sur [0;1] tel que f(0) = f(1)

montrer qu'il existe c de ]0;1[ tel que f(c) = (1-c)/(1+c)

posan h(x)=(1+x)f(x)-(1-x)
h(x) est continu
0<f(0)<1=>f(0)-1<0 =>h(0)<0
0<f(1)<1=> 0<2f(1)<2=> h(1)>0
h(0).h(1)<0 et selon tvi existe un certain c de]0,1[ tels que f(c) =(1-c)/(1+c)

que est ce que tu dis conan?

omis a écrit:

posan h(x)=(1+x)f(x)-(1-x)
h(x) est continu
0<f(0)<1=>f(0)-1<0 =>h(0)<0
0<f(1)<1=> 0<2f(1)<2=> h(1)>0
h(0).h(1)<0 et selon tvi existe un certain c de]0,1[ tels que f(c) =(1-c)/(1+c)

attention les amis , qui a dis que 0=< f(x) =<1

wa 0<f(0)<1 et po f(x)

omis a écrit:

wa 0<f(0)<1 et po f(x)

exactement , explique nous pourqoui ? 0<f(0)<1

ok ds le cours en a une remarque trés importante ke notre prof de math ns la dit
tou les fonctions continue sur un intervale [a,b] sont bornés

ma demo et juste ?? une confirmation

oui c'est juste tout fonction contenue [a;b]est donc borne mais pas borne par 0 et 1 votre demonstration est pas juste et dans l'exercice de manuel il y a une manque des donnes il faut ajoute que f:[0;1]->[0;1]

mohamed_01_01 a écrit:

oui c'est juste tout fonction contenue [a;b]est donc borne mais pas borne par 0 et 1 votre demonstration est pas juste et dans l'exercice de manuel il y a une manque des donnes il faut ajoute que f:[0;1]->[0;1]

c pour cela que j'ai posté cet exo , je voulais savoir exactement s'il y a une solution , ou bien un manque de donnés

donc pose un autre maintenant

bon je le change donc par:
(exo 75 pages 42 almoufid)

soit f et g deux fonction de [0;1] vers [0;1] tel que :

f et g sont continues sur [0:1] et f ([0;1]) = [0:1]


montrer qu'il existe x0 de [0;1] tel que : f(x0) = g(x0)

on supose que h(x)=f(x)-g(x) on f([0;1])=[0;1] donc il ya
f(x0)=0 et f(y0)=1 donc h(x0)=-g(x0)<0 et h(y0)=1-g(x0)>0 donc h(x0)h(y0)<0 d'ou la resultat

bien vu mohamed

tu peux posté ton exo

Conan a écrit:

mohamed_01_01 a écrit:

oui c'est juste tout fonction contenue [a;b]est donc borne mais pas borne par 0 et 1 votre demonstration est pas juste et dans l'exercice de manuel il y a une manque des donnes il faut ajoute que f:[0;1]->[0;1]

c pour cela que j'ai posté cet exo , je voulais savoir exactement s'il y a une solution , ou bien un manque de donnés

si en ajoute cette donné la demo sera juste nn ?

ex 92 page 44
limx->+00(f(x)/x)=1 demontrer que f(x)=x ademet une solution en R+ (desole pour le retatrd)

qq soit epsilon >0 il existe un alpha >0 |f(x)/x-1|<epsilon telque x£R*

==>-x<f(x)<x on suppose
h(x)=f(x)-x ==>

h(x)<0 d'ou e resultat

h(x)<0 c'est pas pour tout x de R+ et bien plus votre demonstration n'est tres claire pour tout les eleve ...rremonce la redaction

badr a écrit:

qq soit epsilon >0 il existe un alpha >0 |f(x)/x-1|<epsilon telque x£R*

==>-x<f(x)<x on suppose
h(x)=f(x)-x ==>

h(x)<0 d'ou e resultat

salut
d'ou tu as eu la relation rouge,?

otman4u a écrit:

badr a écrit:

qq soit epsilon >0 il existe un alpha >0 |f(x)/x-1|<epsilon telque x£R*

==>-x<f(x)<x on suppose
h(x)=f(x)-x ==>

h(x)<0 d'ou e resultat

salut
d'ou tu as eu la relation rouge,?

|f(x)/x-1|<epsilon ==>(-epsilon +1)x<f(x)<x.(epsilon+1)

et j'ai suprimer epsiln puisque il est positive

badr a écrit:

otman4u a écrit:

badr a écrit:

qq soit epsilon >0 il existe un alpha >0 |f(x)/x-1|<epsilon telque x£R*

==>-x<f(x)<x on suppose
h(x)=f(x)-x ==>

h(x)<0 d'ou e resultat

salut
d'ou tu as eu la relation rouge,?

|f(x)/x-1|<epsilon ==>(-epsilon +1)x<f(x)<x.(epsilon+1)

et j'ai suprimer epsiln puisque il est positive

pour le suprimer tu dois donner a epsilon la valeur 0 ce qui est impossible
en + si epsilom est 0 => x=<f(x)=<x et pas -x