| | ******Grand jeu , Inequalities for ever****** |  |
|
+12y-a-ss-i-n-e yassine-mansouri lightshadow codex00 mhdi badr_210 h-o-u-s-s-a-m Figo *pilote militaire * greatestsmaths rachid18 memath 16 participants |
|
| Auteur | Message |
|---|
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 | |
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 02:13 Ven 04 Juil 2008, 02:13 | |
| voici une autre solution:
on met S l expression du cote gauche de l inegalite :
on a ac Chebychev:
S >= {2/3}.(a^3 +b^3 +c^3).({1/a²}+{1/b²}+{1/c²})
=> {2/3}.(a+b+c).(a^3 +b^3 +c^3).({1/a²}+{1/b²}+{1/c²})
=> {2/3}.(a²+b²+c²)²({1/a²}+{1/b²}+{1/c²}) (appliquant C.S)
={2/3}.(a²+b²+c²).(a²+b²+c²).({1/a²}+{1/b²}+{1/c²})
=>6(a²+b²+c²) (tjr C.S)
=> 2 (a²+b²+c² => (a+b+c)²/3 =1/3 )
proposes nous memath ine autre inegalite. | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 02:18 Ven 04 Juil 2008, 02:18 | |
| oké la voila : probleme :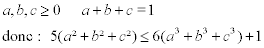 | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 02:33 Ven 04 Juil 2008, 02:33 | |
| voici ma solution:
5(a²+b²+c²)(a+b+c)=5(a^3+b^3+c^3)+5ab(a+b)+5bc(b+c)+5ac(a+c)
on doi prouver que:
a^3+b^3+c^3+1 =>5ab(a+b)+5bc(b+c)+5ac(a+c)
=>a^3+b^3+c^3+ (a+b+c)^3 =>5ab(a+b)+5bc(b+c)+5ac(a+c)
=>a^3+b^3+c^3+3abc => ab(a+b)+bc(b+c)+ac(a+c) ce qui est Schur.
alors???. | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 02:48 Ven 04 Juil 2008, 02:48 | |
| c ussi ma sollution , à toi mntnt  | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 03:18 Ven 04 Juil 2008, 03:18 | |
| ok,voila une autre:
inegalite:
a,b et c des nombres positifs et reels tel que a²+b²+c²=1,prouvez que:
a/(a^3+bc) +b/(b^3+ac)+ c/(c^3+ac) >= 3 | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 03:53 Ven 04 Juil 2008, 03:53 | |
| je vé juste donné mes idees car fia n3aas daba :z: l inegalité equivaut sum(a²/(a^4+abc))>= 3 on a abc=< 1/3V(3) on definie f(x)=x/(x²+1/3V(3)) jé pa calculé mé f a l air convexe loll , donc f(a²)+f(b²)+f(c²)>=3f(1/3)>=3 je vé verifier dem1. bonn nuit  | |
|
  | |
greatestsmaths
Maître

 Nombre de messages : 174 Nombre de messages : 174
Age : 34
Date d'inscription : 22/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 12:06 Ven 04 Juil 2008, 12:06 | |
| Cadeau de mon voyage 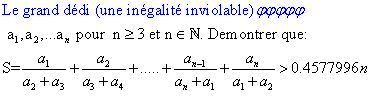 j'ai oublié de dire que les tous a_i>0 | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 13:57 Ven 04 Juil 2008, 13:57 | |
| ou c'est moi qui c est trompé ou ton inegalité est faible. deja pour n=3 l inegalité est plus faible que la classique celle de nessbit. jé fait tt simplement comme ceci : par homogeineté de l inegalité on peut supposer que :  et on a clairement :  et par convexité de x:--> x/(1-x) on a :  | |
|
  | |
greatestsmaths
Maître

 Nombre de messages : 174 Nombre de messages : 174
Age : 34
Date d'inscription : 22/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 15:50 Ven 04 Juil 2008, 15:50 | |
| seulement cette inégalié n'est pas homogéne | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Ven 04 Juil 2008, 17:56 Ven 04 Juil 2008, 17:56 | |
| par definition de l homogeineté je dirai que l inego est homogene | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Sam 05 Juil 2008, 02:13 Sam 05 Juil 2008, 02:13 | |
| @ greatsetmaths : ma sollution est juste .
à moi maintenant :
a,b,c,d>=0 , et a²+b²+c²+d²=1.
trouvez le maximum de :
a^3(b+c+d)+b^3(a+c+d)+c^3(a+b+d)+d^3(a+b+c)
Dernière édition par memath le Mar 08 Juil 2008, 15:22, édité 1 fois | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Dim 06 Juil 2008, 13:25 Dim 06 Juil 2008, 13:25 | |
| alors ??!!! je poste la sollution ?? | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 14:36 Mar 08 Juil 2008, 14:36 | |
| allez les inegosman !!!! un indice , le maximum recherché est 3/4  | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 15:16 Mar 08 Juil 2008, 15:16 | |
| t es sur que tu veux pas dire le minimum? | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 15:23 Mar 08 Juil 2008, 15:23 | |
| desolé jé commi une faute dans l enoncé , c est a²+b²+c²+d²=1 pas abcd=1.
3/4 est le maximum , LHS =< 3/4 | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 15:40 Mar 08 Juil 2008, 15:40 | |
| - memath a écrit:
- @ greatsetmaths : ma sollution est juste .
à moi maintenant :
a,b,c,d>=0 , et a²+b²+c²+d²=1.
trouvez le maximum de :
a^3(b+c+d)+b^3(a+c+d)+c^3(a+b+d)+d^3(a+b+c) LHS=a²(ab+ac+ad)+b²(ab+bc+bd)+c²(ac+cd+bc)+d²(ad+bd+cd) et ac tchebychev on a : LHS <= (1/2)(ab+ac+ad+bc+bd+cd) <= (1/4)(3a²+3b²+3c²+3d²)= 3/4 (j ai utilisé AM-GM dans la deuxième) alors? | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:04 Mar 08 Juil 2008, 16:04 | |
| tu dois verifier que si a>=b>=c>=d on a : ab+ac+bc =< ab+bc+bd =< ac+cd+bc =< ad+bd+cd ce qui n est pas le cas  | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:31 Mar 08 Juil 2008, 16:31 | |
| je pense qu on doit se verifier que si a<= b <= c <=d
on a ab+ac+ad =< ab+bc+bd =< ac+cd+bc =< ad+bd+cd
ce qui est vrai. | |
|
  | |
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:35 Mar 08 Juil 2008, 16:35 | |
| Salut
vous avez demontré que
a^3(b+c+d)+b^3(a+c+d)+c^3(a+b+d)+d^3(a+b+c)=< 3/4
mais faut verifié que la valeur 3/4 est atteinte je croi | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:41 Mar 08 Juil 2008, 16:41 | |
| la valeur 3/4 est atteinte dans le cas ou a=b=c=d=1/V4 | |
|
  | |
Figo
Maître
 Nombre de messages : 196 Nombre de messages : 196
Age : 32
Date d'inscription : 18/09/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:43 Mar 08 Juil 2008, 16:43 | |
| alors est que ma solution est juste? | |
|
  | |
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:47 Mar 08 Juil 2008, 16:47 | |
| il lui manque cette verification ^^ | |
|
  | |
yassine-mansouri
Expert grade1

 Nombre de messages : 426 Nombre de messages : 426
Age : 34
Localisation : Tetouan
Date d'inscription : 18/02/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 16:48 Mar 08 Juil 2008, 16:48 | |
| - memath a écrit:
- la valeur 3/4 est atteinte dans le cas ou a=b=c=d=1/V4
oui c clair mais il faut l'ajouter en tt cas | |
|
  | |
y-a-ss-i-n-e
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 33
Localisation : maroc
Date d'inscription : 21/12/2007
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  Mar 08 Juil 2008, 17:31 Mar 08 Juil 2008, 17:31 | |
| - memath a écrit:
- la valeur 3/4 est atteinte dans le cas ou a=b=c=d=1/V4
mais a²+b²+c²+d²=1 et 4(1/16)=0.25 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: ******Grand jeu , Inequalities for ever****** Sujet: Re: ******Grand jeu , Inequalities for ever******  | |
| |
|
  | |
| | ******Grand jeu , Inequalities for ever****** |  |
|
