| | Préparation Aux Olympiades 2012/2013 |  |
|
+14sadaso ZYGOTO *youness* lamperouge Soukaina Amaadour Ahmed Taha causchy schwarz 47 boubou math Thelastmetalsong9 Gauss-Maxwell k.abdo Humber alidos adeltouzani 18 participants |
|
| Auteur | Message |
|---|
causchy schwarz 47
Féru
 Nombre de messages : 38
Age : 29
Date d'inscription : 11/07/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Lun 10 Déc 2012, 22:25 | |
| ben poste un exo humber ou toi ahmed taha ;;; | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Lun 10 Déc 2012, 22:36 | |
| donc a Mr Humber de poste un exo car hwa lli 7at ljawab hwa lwel  | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| |
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 10:19 | |
| Solution Problème 13- Spoiler:
| |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 12:31 | |
| - *youness* a écrit:
- Solution Problème 13
- Spoiler:
Juste  . A toi de proposer un exercice . | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 13:14 | |
| autre solution :
on pose a=cos^2(x) et b=sin^2(x)
on trouve facilement ab=a^3+b^3 et a+b=1 donc ab(a+b)=a^3+b^3 <=> (a+b)(a-b)^2=0 et en deduir .... | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 13:19 | |
| Proposer une multitude de solutions, oui mais avec une multitude d'exercices aussi  | |
|
| | |
ZYGOTO
Féru
Nombre de messages : 58
Age : 30
Date d'inscription : 19/10/2011
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 13:21 | |
| soit x,y,z>0 montrer que  | |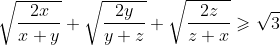
|
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| |
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 18:08 | |
| Solution au problème 14 : - Spoiler:
| |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 18:45 | |
| - *youness* a écrit:
- Problème 14:
 c faciile par Jensen avec f(x)=x/rac(x-1) => f"(x)>0 donc LHS >= 3f(1/3)= rac(3/2) | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 18:59 | |
| - ZYGOTO a écrit:
- soit x,y,z>0
montrer que 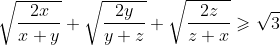L'exercice est faux !
Dernière édition par Humber le Mer 12 Déc 2012, 13:03, édité 3 fois | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 18:59 | |
| - Ahmed Taha a écrit:
- *youness* a écrit:
- Problème 14:
c faciile par Jensen avec f(x)=x/rac(x-1) => f"(x)>0 donc LHS >= 3f(1/3)= rac(3/2) Bien ! Tu n'a qu'à proposer un exercice alors ^^ . Je n'en ai pas pour l'instant . | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 19:18 | |
| | |
|
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 19:44 | |
|
Dernière édition par Humber le Mar 11 Déc 2012, 20:09, édité 1 fois | |
|
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| |
| | |
Humber
Expert grade2
Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 20:10 | |
| | |
|
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mar 11 Déc 2012, 20:22 | |
| | |
|
| | |
*youness*
Maître
Nombre de messages : 132
Date d'inscription : 16/08/2011
| |
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 08:27 | |
| - *youness* a écrit:
- ZYGOTO a écrit:
- soit x,y,z>0
montrer que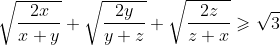
C'est Faux, Essayez Avec x=1, y=80, z=6400
Je Pense L'exo est:
La Solution:
- Spoiler:
c faut khay youness nta byanti blli }) et par nesbit donc }\geq&space;3) maghadi tssa3dek f 7ta 7aja en plus had l'inego deja kayna f l forum ici https://mathsmaroc.jeun.fr/t17181-exercice-d-olympiadeo man3ref chkon lli 7at l'inégo f mathlinks  ww.artofproblemsolving.com/Forum/viewtopic.php?f=52&t=511950&p=2874650#p2874650 | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 08:35 | |
| Problème 15:
Trouver toutes les fonctions f : IR -> IR, telles que pour tout x;y £ IR on ait : f(x²+f(y))=y+f²(x) | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 27
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 14:27 | |
| Pour le Problème 14 , Mr Ahmed taha rah tu as donné une autre inégalité dans le lien que tu as Posté qui est Bien sur très évidente . Bon le Problème 14 a résisté et résiste sur mes tirs qui Proviennent de Mon fusil a Pompe , je vais essayer Bientot avec Mon kalachnikov U6A30 . Solution du Problème 15- Spoiler:
f(x²+f(y))=y+f²(x)
Soit P(x,y) l'assertion f(x²+f(y))=y+f²(x)
P(0,x) f(f(y))=y+f²(0)
posons f(0)=c donc f(f(y))=y+c²
f(x²+f(y))=y+f²(x) donc f(f(x²+f(y)) =f(y+f²(x) )
donc x²+f(y)+c²= f(y+f²(x)) (1)
Posons y=0 donc x²+c+c²=f(f²(x))
donc x²+c²= f(f²(x))-c
Ainsi Dans (1) ça donne f(y+f²(x))=f(f²(x)) +f(y)-c
équivant à f(y+f²(x))-c = f(f²(x))-c + f(y)-c
Posons g(x)=f(x)-c
Via L7aje Cauchy il est facile de voir que g(x)=ax donc f(x)=ax+c
réciproquement la seule fonction qui satisfait l'EF est f(x) =x
N.B : a Lire  | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 20:16 | |
| - alidos a écrit:
- Pour le Problème 14 , Mr Ahmed taha rah tu as donné une autre inégalité dans le lien que tu as Posté qui est Bien sur très évidente . Bon le Problème 14 a résisté et résiste sur mes tirs
qui Proviennent de Mon fusil a Pompe , je vais essayer Bientot avec Mon kalachnikov U6A30 .
Solution du Problème 15
- Spoiler:
f(x²+f(y))=y+f²(x)
Soit P(x,y) l'assertion f(x²+f(y))=y+f²(x)
P(0,x) f(f(y))=y+f²(0)
posons f(0)=c donc f(f(y))=y+c²
f(x²+f(y))=y+f²(x) donc f(f(x²+f(y)) =f(y+f²(x) )
donc x²+f(y)+c²= f(y+f²(x)) (1)
Posons y=0 donc x²+c+c²=f(f²(x))
donc x²+c²= f(f²(x))-c
Ainsi Dans (1) ça donne f(y+f²(x))=f(f²(x)) +f(y)-c
équivant à f(y+f²(x))-c = f(f²(x))-c + f(y)-c
Posons g(x)=f(x)-c
Via L7aje Cauchy il est facile de voir que g(x)=ax donc f(x)=ax+c
réciproquement la seule fonction qui satisfait l'EF est f(x) =x
N.B : a Lire
pour le prob 14 il y a deux solution ma sol et la sol de Mr Humber et le lien c la solution du prob de Mr ZYGOTO + BRAVO et MERCI pour ta sol donc a toi de poster un exo | |
|
| | |
alidos
Expert grade2
Nombre de messages : 352
Age : 27
Localisation : Goulmima
Date d'inscription : 04/02/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 21:12 | |
| de rien ^^ , Konte na9sséd le Problème 14 celui de Zygoto j'ai vu que Mr younéss a dit que c'est faux . j'ai bien galérer avec cette inégalité . pour l'inégalité LHS=< 3 c'est elle a qui j'ai dit qu'elle est évidente, Bon .pour accélèrer ce Marathon Again je Propose ce Problème. Problème 16 Résoudre dans IN ^{3}=(x-y-6)^2) | |
|
| | |
Ahmed Taha
Maître
Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 Mer 12 Déc 2012, 22:00 | |
| - alidos a écrit:
- de rien ^^ , Konte na9sséd le Problème 14 celui de Zygoto j'ai vu que Mr younéss a dit que c'est faux . j'ai bien galérer avec cette inégalité . pour l'inégalité LHS=< 3 c'est elle a qui j'ai dit qu'elle est évidente, Bon .pour accélèrer ce Marathon Again je Propose ce Problème.
Problème 16
Résoudre dans IN
ah bon Solution probleme 16 puisque x,y£IN donc x+y=<|x-y-6| => x=<3 x=0 => p(y)=y^3-y^2-12y-36=0 pour p(4)<0 et p(5)>0 et p tazayodya donc S_1={} de meme pour x£{1,2,3} on trouve finalement S={(1,3)} P.S c un exo du troisieme test d l'annee dernier | |
|
| | |
Contenu sponsorisé
| | Sujet: Re: Préparation Aux Olympiades 2012/2013 | |
| |
|
| | |
| | Préparation Aux Olympiades 2012/2013 | |
|
