| | ***Grand Jeu D'été de T.C->Première*** |  |
|
+35xyzakaria samix Ayoub M-H l_Soufiane_l ll_Ayoub_ll smash Galois 94 n.naoufal marouan777 {}{}=l'infini soukki memath Hajar'S anass-sci Figo red11 hunter Kabylia merkam abdellah=einstein khalid545 oussama1305 houssa Afaf ziko00212 MohE amjad92b La volonté MouaDoS meryeem sweet-mounir HMXXMH houssam110 majdouline mathsmaster 39 participants |
|
| Auteur | Message |
|---|
La volonté
Maître
 Nombre de messages : 115 Nombre de messages : 115
Age : 31
Date d'inscription : 15/05/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Jeu 09 Juil 2009, 22:57 Jeu 09 Juil 2009, 22:57 | |
| | |
|
  | |
La volonté
Maître
 Nombre de messages : 115 Nombre de messages : 115
Age : 31
Date d'inscription : 15/05/2009
 | |
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Jeu 09 Juil 2009, 23:36 Jeu 09 Juil 2009, 23:36 | |
| solution du problème:
soit H le projeté orthogonal de A sur [BC]
AH=h
considérons le triangle AHC:
d'apres Pythagore on a :
h²=b²-HC² (1)
------------------------------
considérons ABH:
h²=c²-BH² (2)
--------------------------------
de (1) et (2) on a :
2h²=b²c²+-(CH²+BH²)
<=>4h²=2b²+2c²-2(CH²+BH²) *
-----------------------------------------------
on sait que :
2(CH²+BH²)≥(CH+BH)²=a²
<=>2(CH²+BH²)≥a²
alors -2(CH²+BH²)≤-a² **
------------------------------------------------
de * et ** on a :
4h²≤2b²+2c²-a²
Dernière édition par majdouline le Jeu 09 Juil 2009, 23:43, édité 1 fois | |
|
  | |
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Jeu 09 Juil 2009, 23:37 Jeu 09 Juil 2009, 23:37 | |
| Salut,
Liakoun H lmas9it l3amoudi li A 3ala (BC):
(BH-CH)²>=0
BH²+CH²-2BH*CH>=0
2BH²+2CH²-(BH+CH)²>=0
2BH²+2CH²-a²>=0
ns avons:BH²=c²-h² CH²=b²-h²
on remplaçant:4h² | |
|
  | |
red11
Expert sup

 Nombre de messages : 674 Nombre de messages : 674
Age : 31
Date d'inscription : 28/06/2007
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Jeu 09 Juil 2009, 23:38 Jeu 09 Juil 2009, 23:38 | |
| Oups desolé majdouline( poste your exercise) | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Ven 10 Juil 2009, 11:27 Ven 10 Juil 2009, 11:27 | |
| bJr..... xd...1 minute  dsl de vous faire attendre...on continue encore avec la géométrie  problème proposé: soit ABC un triangle isocele en A....la bissectrice de de l'angle ABC coupe [AC]en D tel que:BC=AD+BD.... problème proposé: soit ABC un triangle isocele en A....la bissectrice de de l'angle ABC coupe [AC]en D tel que:BC=AD+BD....
trouver la mesure de l'angle BACgood luck  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mar 14 Juil 2009, 11:33 Mar 14 Juil 2009, 11:33 | |
| bJr.... dsl  ....je crois que vous aurez besoin de la relation suivante: sinA.cosB=1/2*[sin(A+B)+sin(A-B)] donc je vous donne encore plus de temps...mais qui sait vous pouvez trouver une solution sans utiliser cette relation!!!!!  | |
|
  | |
La volonté
Maître
 Nombre de messages : 115 Nombre de messages : 115
Age : 31
Date d'inscription : 15/05/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 13:38 Mer 22 Juil 2009, 13:38 | |
| Bonjour On doit continuer. voilà un exercice: 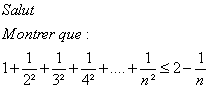 | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 14:15 Mer 22 Juil 2009, 14:15 | |
| nn c pas toi qui doit poster j vais poster la solution du probleme ce soir accompagné d'un nouveau probleme!!!!!! | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 14:16 Mer 22 Juil 2009, 14:16 | |
| bonjour . soit k app à IN - {0,1} . puisque , 0 < k(k-1) =< k^2 alors on a : 1/k^2 < 1/k(k-1) . ce qui veut dire : 1/k^2 < 1/k-1 - 1/k . donc par sommation de 2 à n on trouve : 1/2^2 + 1/3^2 + ..... + 1/n^2 =< 1 - 1/n . c'est à dire : 1 + 1/2^2 + 1/3^2 + ..... + 1/n^2 =< 2 - 1/n cqfd . @ +  . | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 16:22 Mer 22 Juil 2009, 16:22 | |
| oué c ça Galois94  ....ou bien avec la récurrence ....on demontre que c vrai pour n=1 et n=2 et puis on suppose que c vrai pour n et on démontre que c vrai pour n+1...c simple...il existe plusieurs méthodes  | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 18:20 Mer 22 Juil 2009, 18:20 | |
| | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 | |
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 20:34 Mer 22 Juil 2009, 20:34 | |
| C'est super facile, allez les gars ...  | |
|
  | |
xyzakaria
Expert grade2
 Nombre de messages : 374 Nombre de messages : 374
Age : 31
Date d'inscription : 12/12/2008
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 20:52 Mer 22 Juil 2009, 20:52 | |
| slt^^ majdouline j vois pas l image><. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 20:57 Mer 22 Juil 2009, 20:57 | |
| ok ziko...voici l'exo ...résoudre dans IR: x=2[sqrt{x-2}]+3  | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 21:40 Mer 22 Juil 2009, 21:40 | |
| bonsoir : on a : D = [2,+00[ . pour x app à D on a : [V(x-2)] = (x-3)/2 . or , [V(x-2)] app à IN ==> (x-3)/2 = k ==> x = 2k+3 où k app à IN . et par suite on aura : [V(2k+1)] = k . autrement dit , k =< V(2k+1) < k+1 . ie k^2 - 2k-1 =< 0 et k^2 > 0 . ie (k-1)^2 =< 2 et k app à IN - {0} . ie |k -1| =< V2 et k app à IN - {0} . ie k = 1 ou k = 2 . donc , S = {5;7} . @ +  . | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 22:18 Mer 22 Juil 2009, 22:18 | |
| bonne solution Galois94  ...c'est à toi mnt!!!! | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 22:33 Mer 22 Juil 2009, 22:33 | |
| dsl explique moi comment il as trouvé " k^2 - 2k-1 =< 0 " | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Mer 22 Juil 2009, 23:15 Mer 22 Juil 2009, 23:15 | |
| bonsoir marouan777 . on a : a =< x =< b <==> a =< x et x =< b . or , k=<V(2k+1) < k+1 <==> k =< V(2k+1) et V(2k+1) < k+1 . <==> k^2 =< 2k+1 et 2k+1 < (k+1)^2 <==> .......... je crois que c'est claire maintenant marouan . @ +  . | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Jeu 23 Juil 2009, 02:55 Jeu 23 Juil 2009, 02:55 | |
| bonsoir . soit f une fonction définie sur IR et vérifiant : f(x+2) = f(x-1).f(x+5) , pour tout x dans IR . Montrer que f est périodique . @ +  . | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Ven 24 Juil 2009, 13:58 Ven 24 Juil 2009, 13:58 | |
| solution du probleme:(pas sure)
1)-définition:
soit f une fonction
f est dite périodique si pour tout x de Df on a : x+p£Df
tel que: f(x)=f(x+p)
--------------------------------------------------------------
ma solution(sauf erreur)se base sur le changement de variable:
on a f(x+2)=f(x-1).f(x+5)
posons x+2=X...on obtient alors:
f(X)=f(X-3).f(X+3)
f(x)=f(x-3).f(x+3) (1)
-------------------------------------------------------------------
posons maintenant x=X-3
--->f(X-3)=f(X-6).f(X)
f(x-3)=f(x).f(x-6) (2)
----------------------------------------------------
on a :f(x)=f(x-3).f(x+3)
posons x=X+3
f(X+3)=f(X).f(X+6)
f(x+3)=f(x).f(x+6) (3)
-------------------------------------------------------------------
si f(x-3) et f(x-3) sont non nuls:
alors f(x) et non nulle aussi car :f(x)=f(x-3).f(x+3)
multiplions (1) par (2):
f(x).f(x-3)=f(x-3).f(x+3).f(x).f(x-6)
alors:f(x+3).f(x-6)=1
f(x-6)=1/f(x+3)
<=>f(x-9)=1/f(x) (a)
-----------------------------------------------------------------------------
multiplions mnt (1) par (3):
f(x).f(x+3)=f(x-3).f(x+3).f(x).f(x+6)
alors f(x-3).f(x+6)=1
f(x+6)=1/f(x-3)
f(x+9)=1/f(x) (b)
------------------------------------------------
de (a) et (b) on a :
f(x-9)=f(x+9)
f(x)=f(x+18)
on a Df=IR
alors x+18£Df
et on a : f(x+18)=f(x)
alors f est périodique
-----------------------------------------------
maintenant si f(x-3) ou f(x+3) sont nuls...
on a :f(x)=f(x-3).f(x+3)
alors f(x)=0
d'où f(x+p)=0
f(x+p)=f(x)
pour tout p£IR --->p£Df
alors f est périodique
-----------------------------------------------------
dans tous les cas on a :f est périodique
Dernière édition par majdouline le Ven 24 Juil 2009, 18:18, édité 3 fois | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Ven 24 Juil 2009, 16:27 Ven 24 Juil 2009, 16:27 | |
| bonjour . c'est ça l'idée majdouline , mais regarde l'égalité ( 3 ). on a : f(x+3) = f(x).f(x+6) et non pas f(x).f(x-6) !!!!! . @ +  . | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Ven 24 Juil 2009, 16:29 Ven 24 Juil 2009, 16:29 | |
| merci bien galois94 pour votre indication erreur d'inattention j vais la corriger immediatement | |
|
  | |
Galois 94
Maître
 Nombre de messages : 157 Nombre de messages : 157
Age : 30
Date d'inscription : 26/06/2009
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  Ven 24 Juil 2009, 16:39 Ven 24 Juil 2009, 16:39 | |
| bonjour : il ya tjs une erreur majdouline , essaye de la trouver la période n'est pas : 12 . @ +  . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: ***Grand Jeu D'été de T.C->Première*** Sujet: Re: ***Grand Jeu D'été de T.C->Première***  | |
| |
|
  | |
| | ***Grand Jeu D'été de T.C->Première*** |  |
|
