Préparations aux olympiades de tronc commun (2009-2010)

Heu oui tu a raison désolé c'est une faute d'innatention je corrige !!

C'est un exo de T-C , Pas besoin d'utiliser un récurrence ^^

Dijkschneier a écrit:

qui ne semble pas être aussi parfait que ça..

codex00 a écrit:

Pourquoi ca ne semble po être un carré parfait ?

Ensuite, on sait que :

Or, et (les nombres ne se terminent pas par un 5), donc
Ainsi, puisque l'exposant de 5 est impair, n ne peut être un carré parfait

Slt tu pourrais m'expliquer stp ce que tu veut dire par tout les exposants de sa decomposition en facteurs premié sont pairs ; et merci ^^

si jamais A est carré parfait et a/A et b/A
alors A=a^(2n) x b^(2m) x c^(2k)

darkpseudo a écrit:

Slt tu pourrais m'expliquer stp ce que tu veut dire par tout les exposants de sa decomposition en facteurs premié sont pairs ; et merci ^^

Soit A un entier. La décomposition en facteurs premiers de A est unique et s'écrit : tels que est une suite d'entiers naturels non nuls et une suite de nombres premiers.
Maintenant :

Merci pour la regle que je connaissais pas ^^ c'est gentil a vous deux

Je ne sais pas si ma précédente solution a été approuvé. Je me risque toutefois, non sans péril, à lancer un nouveau problème :
Problème :
Soit a, b et c des réels strictement positifs.
Montrer que :

Ta solution est acceptable mais il existent d'autre plus simple ^^

Par exemple :

Autre façon de dire la même chose :

Le nombre N peut s'écrire :
N=2000(1+2000(1+2000(…etc…)))
avec 2000=2x2x2x2x5x5x5
Le terme multiplicateur de 2000 n'est divisible ni par 2 ni par 5 (car il est obtenu en ajoutant 1 à un multiple de 2 et de 5).
N ne peut pas être un carré parfait car 5x5x5 n'est pas un carré.
N ne peut pas être un cube car 2x2x2x2 n'est pas un cube.
Et plus généralement, il ne peut pas être écrit sous la forme d'une
puissance entière N=n^p avec p>3 car ni (2x2x2x2) ni (5x5x5) ne
peuvent l'être.
Conclusion: N ne peut pas se mettre sous la forme d'une puissance entière N=n^p, quelque soit p>1.

Dijkschneier a écrit:

Je ne sais pas si ma précédente solution a été approuvé. Je me risque toutefois, non sans péril, à lancer un nouveau problème :
Problème :
Soit a, b et c des réels strictement positifs.
Montrer que :

D'après chebychev + AM-GM



donc il suffit de prouver que :



et par AM-GM on a :



avec égalité si a=b=c

Sois ABC un triangle et BD le médiatrice du ségment [AC]

tel que : l'angle DBC=BAD=x et BDA=45°

TRouver x .

samix a écrit:

Sois ABC un triangle et BD le médiatrice du ségment [AC]

tel que : l'angle DBC=BAD=x et BDA=45°

TRouver x .

C'est faux BDA=90° (médiatrice=واسط).

Si c'est juste déssinez la figure.

samix a écrit:

D'après chebychev + AM-GM

Je ne pense pas que ce passage soit tout à fait correcte.. Pour pouvoir utiliser Chebyschev de la sorte, les suites doivent être toutes deux croissantes ou toutes deux décroissantes. Ainsi, si tu supposes , on ne peut avoir :

Oui même avis >.<
Mais si j'arrive pas à trouver un contre-exemple ^^

Je pense que Samix a une explication pour ca

Contre exemple :

solution de l'inégalité proposée:
il est bien remarquable que l'inégalité est homogène (car f(a,b,c)=f(ka,kb,bc)
on peut donc supposer que abc=1
l'inégalité devient:

commençons par prouver (1) :

par Am-Gm on a:

alors:

-------------------------------------------------------------------------------
revenons à l'inégalité qu'on veut démontrer
depuis (1) il suffit de prouver que :

notons a+b+c=X
l'inégalité est équivalente à:
p(X)=X²-4X+3≥0
delta=2²
X1=1 et X2=3
alors P(X) est positif sur [3,+00[
or par Am-Gm on a : a+b+c≥3 (car abc=1)
CQFD .....

Bravo ! Ta preuve est quasiment similaire à la mienne. Toutefois, pour montrer que , j'ai plutôt utilisé le lemme de Titu..

samix a écrit:

Sois ABC un triangle et BD le médiatrice du ségment [AC]
tel que : l'angle DBC=BAD=x et BDA=45°
TRouver x .

J'ai bien trouvé que x=15° mais je n'arrive plus à la démontrer.
Je vous propose cet exercice:
x est un réel vérifiant x^2-x-1=0.
Trouvez des réels a et b tels que x^10=ax+b.
Bonne chance.

Donc, et

Dijkschneier a écrit:

Donc, et

C'est vrai. J'attend ton exercice.
Ou il est autorisable à tout le monde de poster. J'attend, sinon je poste le mien à 17 heures.

Remarque pour l'exo :
a et b sont des nombres de la suite Fibonacci

Sylphaen a écrit:

Remarque pour l'exo :
a et b sont des nombres de la suite Fibonacci

Ça va de soi !

Je propose ce problème :
Problème :
Soient 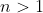et tels que
Prouver que :

V(1-Xi) =>1-Xi≥1 ce qui implique que tous les Xi sont égal à 1.

Y'a t-il pas une erreur ?