| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 16:05 Lun 14 Déc 2009, 16:05 | |
| Bon bein si tu veut po poster je poste ^^ :
soi AB et DC deux segment du plan tel que A,B,C, et D sont différents
dessinez touts les cercles auxquels appartient les quatres A,B,C,D
( avec justification )
Et trouvez le cas ou il ne pourra pas y avoir de cercle qui rempli la consigne !!
Dernière édition par darkpseudo le Lun 14 Déc 2009, 17:37, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 17:36 Lun 14 Déc 2009, 17:36 | |
| Le premier cas CAB+CDA=180°.
On dessine la médiatrice du segment AD et la médiatrice du segment BC. Le point d'intersection est le centre du cercle qui entoure A,B,C,D.
Le cas où on ne peut pas entourer les points A,B,C,D avec un cercle est celui où CAB+CDA#180°.
J'espère que c'est juste.
J'attends ta confirmation.
Dernière édition par nmo le Mer 23 Juin 2010, 11:11, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 17:39 Lun 14 Déc 2009, 17:39 | |
| Dsl mais c'est faux ; au fait la question c'est pas de me trouver un cas particulier mais de dessinez les deux segment a main levez et puis de trouver une facon de dessiné les cercles | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 17:57 Lun 14 Déc 2009, 17:57 | |
| Voici la méthode avec laquelle j'ai résolu mon exercice.
On a m+n=p
Donc m+n+mn=p+mn
Donc m+n+mn+1=p+1+mn.
Donc m(1+n)+1+n=mn+mn.
Donc (m+1)(n+1)=2mn.==>(a)
Du fait que m+n=p
On a m=p-n.
Donc m+1=p+1-n.
Ensuite m+1=mn-n.
Enfin m+1=n(m-1).==>(1)
De même n+1=m(n-1).==>(2)
Et lorsqu'on remplace 1 et 2 dans a
On trouve m(n-1)n(m-1)=2mn.
Donc (n-1)(m-1)=2.====>parceque m#0 et n aussi.
Les diviseur de 2 sont 1 et 2.
Donc on a deux cas (n-1)=1 et (m-1)=2 ou (n-1)=2 et (m-1)=1.
Le premier cas:
On a n-1=1 et m-1=2.
Donc n=2 et m=3.
Le deuxième cas
On a n-1=2 et m-1=1.
Donc m=2 et n=3.
Finalement p=3+2=2+3=5.
Que diras-tu darkseudo?
Je n'ai pas compri ta méthode.
Dernière édition par nmo le Mer 23 Juin 2010, 11:15, édité 2 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 18:00 Lun 14 Déc 2009, 18:00 | |
| - darkpseudo a écrit:
- Dsl mais c'est faux ; au fait la question c'est pas de me trouver un cas particulier mais de dessinez les deux segment a main levez et puis de trouver une facon de dessiné les cercles
Je n'ai pas compri. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 18:17 Lun 14 Déc 2009, 18:17 | |
| Pour te faciliter la tache ^^ ... Je vais donner une partie de la réponse :
On cherche un point M tel que : AM=BM=CM=DM
tu voit donc ce point sera le centre d'un cercle est ce cercle aura pour rayons : AM et BM et CM et DM
sachant que A et B et C et D sont différents les uns des autres et que AB et CD ne font pas parti de la même droite trouve moi un cas ou ces deux segment ne seront inscrit par aucun cercle ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 18:26 Lun 14 Déc 2009, 18:26 | |
| Je pense que lorsqe l'une des segments est perpendiculaire sur l'autre. J'attends ta confirmation. et un point est lemilieu du segments.
Exemple AB est perpendiculaire sur CD et B est le milieu de CD.
Dernière édition par nmo le Lun 14 Déc 2009, 18:39, édité 1 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 18:35 Lun 14 Déc 2009, 18:35 | |
| tu n'as trouvé qu'un cas particulié ^^ et tu n'as pas répondu a la premiére question ; or pour répondre a la deuxiéme faut savoir répondre a la premiére et justifié ta réponse !! Puisque ya po tro de monde je te laisse une derniére chance apré je repondrais ^^ Au fait cette exo c'est un prof qui me l'as donné et tu verra aprés que c'est pas difficil il faut juste savoir commencer ^^ bonne chance a toi | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 18:41 Lun 14 Déc 2009, 18:41 | |
| Je pense que lorsque trois point sont allignés.J'attend ta confirmation. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 19:17 Lun 14 Déc 2009, 19:17 | |
| Voici un exercice très dur:
Troits robinets à débits constant alimentent un réservoir.
On ouvre deux seulement des trois robinets;
le réservoir est rempli en 30 minutes.
Lorsque l'on ouvre deux autres il est rempli en 35 minutes
et quand on en ouvre encore deux autres il est remli en 42 minutes.
1/Quel temps faut-il à chacun des robinets pour remplir seul le réservoir?
2/Lorsque les trois robinets sont ouverts combien de temps faut-il pour remplir le réservoir?
3/Le robinets dont le débits est le plus fort débite 20 litres de moins à la minute que les autres réunis
Calculez la capacité du réservoir.
Bonne chance.
Dernière édition par nmo le Ven 28 Jan 2011, 14:50, édité 2 fois | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 14 Déc 2009, 19:49 Lun 14 Déc 2009, 19:49 | |
| Bon bein deja pour mon probléme ^^ il n'y a pas de cercle lorsque les médiatrice de AB et BC et CD et AD ne se son pas concourantes ( elles ne se croisent pas en un point ) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 20 Déc 2009, 15:29 Dim 20 Déc 2009, 15:29 | |
| Je vais vous attendre jusqu'à jeudi prochain et je posterai ma réponse. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 25 Déc 2009, 14:41 Ven 25 Déc 2009, 14:41 | |
| Comme il y avait hier les coupures d'électricité je n'ai pas pu poster la solution, je la posterai dans quelques temps.
Attendez un peu.
Dernière édition par nmo le Mer 23 Juin 2010, 11:17, édité 1 fois | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 25 Déc 2009, 14:56 Ven 25 Déc 2009, 14:56 | |
| salam
pour darkpseudo
ton texte n'est pas l'original
donc tu as mal rédigé l'énoncé
il fallait tout simplement demander :
quelle condition sur A,B,C et D pour que l'on puisse faire passer un cercle
par les 4 points
la réponse : il suffit que 3 des médiatrices soient concourantes.
. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 25 Déc 2009, 15:18 Ven 25 Déc 2009, 15:18 | |
| Soit x,y,z les débits respectifs des trois robinets, exprimés en litre par minutes et soit R la capacité du réservoir en litres.
Les deux premiers robinets coulent pendant 30 minutes, donc le premiers fourit 30x litres et le deuxième 30y litres avec 30x+30y=R.
Nous obtenons deux autres équations de la même façon et finalement nous sommes conduits à la résolution du système:
x+y=R/30.
y+z=R/35.
z+x=R/42.
De la première équation nous tirons x=(R/30)-y
et si nous remplaçons dans la troisième équation nous obtenons le système équivalent
x=(R/30)-y.
y+z=R/35.
-y+z=(R/42)-(R/30)=-(R/105).
La résolution du système formé par les deux dernières équations donne z=R/105 et y=2R/105 et vous trouverez x=R/70.
Si en une minutes le troisième robinet remplit le 1/105 du réservoir il lui faudra 105 minutes pour le remplir complètement.
De même il faudra 52.5 minutes pour le second et 70 minutes pour le premier.
2/Lorsque les trois robinets sont ouverts en même temps ils coulent pendant une durée t qui est bien sûr identique pour les trois.
On obtiendra alors l'équation: (R/70)t+(2R/105)t+(R/105)t=R.
équivalente à (3/70)t=1.
ILfaut donc 70/3, soit environ 23 minutes , aux trois robinets pour remplir le réservoir.
3/C'est le premier robinet qui a le plus fort débits donc x+20=y+z.
donc (R/70)+20=(2R/105)+(R/105) en résulte qui donne R=1400 litres.
Sauf erreur.
Dernière édition par nmo le Mer 23 Juin 2010, 11:18, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 25 Déc 2009, 15:23 Ven 25 Déc 2009, 15:23 | |
| Voilà un exercice plus simple:
Factorisez A sachant que:
A=(a^2)(b-c)+(b^2)(c-a)+(c^2)(a-b)
Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 25 Déc 2009, 20:14 Ven 25 Déc 2009, 20:14 | |
| 3 factorisations sont envisageables. Par exemple : (ab+ac+bc-a^{2})) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 15:04 Sam 26 Déc 2009, 15:04 | |
| - Dijkschneier a écrit:
- 3 factorisations sont envisageables.
Par exemple : (ab+ac+bc-a^{2})) Il faut terminer la factorisation. Réessaye. Il y a une seule factorisation.
Dernière édition par nmo le Mer 23 Juin 2010, 11:08, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 16:18 Sam 26 Déc 2009, 16:18 | |
| A=(b+c)(ac-ab)+(b-c)(a²+bc)
=(b+c).a(c-b)+(b-c)(a²+bc)
=(b-c)(a²+bc-ab-ac)
=(b-c)(a-c)(a-b) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 16:26 Sam 26 Déc 2009, 16:26 | |
| C'est vrai Sylphaen.
A toi de poster un exo ou quelqu'un d'entre vous.
Dernière édition par nmo le Mer 23 Juin 2010, 11:08, édité 1 fois | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 16:37 Sam 26 Déc 2009, 16:37 | |
| Soit n £ [N un nombre tels que :
n= 2000 2000 ..... 2000
Le nombre 2000 se répète 2000 fois .
Est ce que n est un carré parfait ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 17:44 Sam 26 Déc 2009, 17:44 | |
| %20\\%20&=%202000%20\times%20\frac{(10^{3})^{2001}-1}{10^{3}-1}%20\\%20&=%20\frac{2000}{999}\times(10^{6006}-1)%20\\%20&=%20\frac{2000}{999}\times999...9%20\\%20&=%20\frac{2000}{111}\times111...1%20\end{align*}) qui ne semble pas être aussi parfait que ça.. | |
|
  | |
codex00
Expert sup

 Nombre de messages : 2122 Nombre de messages : 2122
Age : 34
Localisation : No where !!!
Date d'inscription : 30/12/2006
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 26 Déc 2009, 21:11 Sam 26 Déc 2009, 21:11 | |
| Pourquoi ca ne semble po être un carré parfait  ? | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 27 Déc 2009, 12:18 Dim 27 Déc 2009, 12:18 | |
| montrons par récurence montrons que : 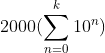 n'est pas un carré parfait pour k=0 2000 n'est pas un carré parfait supposont que c'est vrai pour n et montrons que sa l'est aussi pour n+1 donc montrons que :  n'est pas un carré parfait on a  puisque cette somme n'est jamais un carré parfait donc la récurence est juste ^^ Enfin je pense !!
Dernière édition par darkpseudo le Dim 27 Déc 2009, 13:18, édité 1 fois | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 27 Déc 2009, 12:30 Dim 27 Déc 2009, 12:30 | |
| Ta récurrence ne semble pas avoir été très bien construite : l'hérédité devrait normalement se faire de la sorte : %20\text%20{%20n%27est%20pas%20parfait%20}) | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
