| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 21:58 Sam 27 Mar 2010, 21:58 | |
| Sinon , on peut remarquer que :
1/2·3/4·5/6· ... ·99/100 < 1/10
Il suffit donc de la prouver.
----------------------------------------------------------------------------
Posons : A = 1/2·3/4·5/6· ... ·99/100. et B = 2/3·4/5·6/7· ... ·98/99.
2/3 > 1/2, 4/5 > 3/4, ..., 98/99 > 97/98, 1 > 99/100.
à partir de ce dérnier on a : A < B. Donc : AB = 1/100 (1) ( en simplifiant en utilisant l'observation .. )
Alors : A2 < AB < 1/100, et on se retourne plus géneral :
1/2·3/4·5/6· ... ·(2n-1)/2n < 1/(2n), (2)
A(n) = 1/2·3/4·5/6· ... ·(2n-1)/2n,
B(n) = 2/3·4/5·6/7· ... ·(2n-2)/(2n-1).
A(n) < 1/(3n+1). (3)
ce qui donne : (3') A(n) < 1/(3n),
-------------------------------------------------------------
Et on a A(1) = 1/2 = 1/(3·1+1).
ce qui est faux avec 2
Car : A(2) = 1/2·3/4 = 3/8 < 1/7 = 1/(3·2+1),
Faisant le carré :
9/64 < 1/7,pour 7·9 = 63 < 64
Posons : n=k
(4) A(k) < 1/(3k+1).
Et on prouve que n=k+1
(5) A(k+1) < 1/(3(k+1)+1) = 1/(3k+4).
et parceque : A(k+1) = A(k)·(2k+1)/(2k+2), (4)
Il parait clairement que : (6) A(k+1) < (2k+1)/(2k+2)·1/(3k+1).
---------------------------------------------------------------------------
Et mtn on fait le carré du coté droit :
[(2k+1)/(2k+2)·1/(3k+1)]2 = (2k+1)2 / ((2k+2)2(3k+1))
= (2k+1)2 / (12k3 + 28k2 + 20k + 4)
= (2k+1)2 / [(12k3 + 28k2 + 19k + 4) + k]
= (2k+1)2 / [(2k+1)2(3k+4) + k]
< (2k+1)2 / [(2k+1)2(3k+4)]
= 1 / (3k+4),
Qui est exactement le coté droit de (5) et qui prouve (6)
Enfin , on peut finir et trouver clairement le résultat. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 | |
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 22:06 Sam 27 Mar 2010, 22:06 | |
| Donc calculez-moi : EX 1:   EX2: a+b+c=abc,M.Q:a(1-b²)(1-c²)+b(1-a²)(1-c²)+c(1-a²)(1-b²)=4abc. Bonne chance. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 | |
  | |
zouhir
Féru
 Nombre de messages : 55 Nombre de messages : 55
Age : 33
Date d'inscription : 14/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 22:47 Sam 27 Mar 2010, 22:47 | |
| la premiére foit LaTeX sur mathsmaroc | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 29 Mar 2010, 15:25 Lun 29 Mar 2010, 15:25 | |
| - M.Marjani a écrit:
- Donc calculez-moi :

EX2:
a+b+c=abc,M.Q:a(1-b²)(1-c²)+b(1-a²)(1-c²)+c(1-a²)(1-b²)=4abc.
Bonne chance. - Spoiler:
Sauf erreur.  Au plaisir ! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 29 Mar 2010, 18:49 Lun 29 Mar 2010, 18:49 | |
| - mizmaz a écrit:
- M.Marjani a écrit:
- Donc calculez-moi :

EX2:
a+b+c=abc,M.Q:a(1-b²)(1-c²)+b(1-a²)(1-c²)+c(1-a²)(1-b²)=4abc.
Bonne chance. - Spoiler:
Sauf erreur. 
Au plaisir ! C'est juste. Mais j'ai pas compris la methode oO + j'ai dis (1-1/4) , t'as écris (1-1/2^3) et t'as trouvé le méme résultat oO Vous pouvez m'expliquez ce truc. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 | |
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 29 Mar 2010, 21:48 Lun 29 Mar 2010, 21:48 | |
| - M.Marjani a écrit:
- Donc calculez-moi :
EX2:
a+b+c=abc,M.Q:a(1-b²)(1-c²)+b(1-a²)(1-c²)+c(1-a²)(1-b²)=4abc.
Bonne chance. - Spoiler:
Sauf erreur.  Au plaisir ! | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 30 Mar 2010, 15:08 Mar 30 Mar 2010, 15:08 | |
| - mizmaz a écrit:
- M.Marjani a écrit:
- Donc calculez-moi :
EX2:
a+b+c=abc,M.Q:a(1-b²)(1-c²)+b(1-a²)(1-c²)+c(1-a²)(1-b²)=4abc.
Bonne chance. - Spoiler:
Sauf erreur. 
Au plaisir ! C'est juste , trés bien mizmaz. Une petite remarque : pour démontrer une résultat, on parti d'une coté pour démontrer l'autre coté. A vous de postez. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 30 Mar 2010, 17:09 Mar 30 Mar 2010, 17:09 | |
| Okay. Calculez :  Le truc continue jusqu'à l'infini.  | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 30 Mar 2010, 21:45 Mar 30 Mar 2010, 21:45 | |
| On pose @=RAC(1+RAC(1+RAC(1+...
Donc @=RAC(1+@)
On élève au carré @²=1+@
Equivalent de @²-@-1=0
Delta, discriminant, égale (-1)²-4(1)(-1)=1+4=5
Racine du discriminant égale RAC(5)
Les deux solutions de cette équation sont
@1=-(-1)-RAC(5)sur2(1)=(1-V5)/2
@2=-(-1)+RAC(5)sur2(1)=(1+V5)/2
On élimine @1 qui est négatif, ce qui nous laisse le nombre d'or | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 30 Mar 2010, 22:26 Mar 30 Mar 2010, 22:26 | |
| Exact !  A toi. | |
|
  | |
Calculus
Féru
 Nombre de messages : 49 Nombre de messages : 49
Age : 30
Date d'inscription : 26/02/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 30 Mar 2010, 23:07 Mar 30 Mar 2010, 23:07 | |
| | |
|
  | |
oussama1305
Expert grade1

 Nombre de messages : 443 Nombre de messages : 443
Age : 32
Localisation : Casablanca
Date d'inscription : 25/05/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 13:16 Mer 31 Mar 2010, 13:16 | |
| Voir que 4 est une racine évidente. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 18:23 Mer 31 Mar 2010, 18:23 | |
| - Sylphaen a écrit:
- La factorisation est un peu magik ^^ sinon voici une autre solution pour l'équation :
On fixe y=1/x on se ramène à :
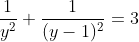
Pour équilibrer ( avoir une équation de 2éme degré) on pose z=y-1/2
Ca donne :
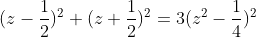
encore un changement de variable : a=z²>=0
ca donne :
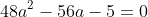
La solution positif est a=5/4
Puis on trouve aisément les valeurs de x Voici une solution plus simple: On a ^2}=3) . On pose x=y+1. Cette équation équivaut à ^2+\frac{(y+1)^2}{y^2}=3) . Donc  . Donc  . Donc  . Maintenant, on pose t=y+1/y. Cette équation équivaut de nouveau à  . Et finalement  . Et il ne reste que calculer le discriminent et remplacer pour trouver les valeurs de x. P.S: les résultats en hauts sont justes.
Dernière édition par nmo le Jeu 01 Avr 2010, 17:54, édité 1 fois (Raison : Faute) | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 18:57 Mer 31 Mar 2010, 18:57 | |
| Bonne idée nmo mais il ya une petite faute que tu viens de faire : ^2+\frac{(y-1)^2}{y^2}=3) Il faudrait faire (y-2)² à la place de y² ( voir au dénominateur ) + dans la prochaine étape t'as fais (y-1)²=y²-2x+1 S'il est juste une éxplication , car tu sais plus que moi ce que t'as fait  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 19:05 Mer 31 Mar 2010, 19:05 | |
| On peut utiliser la dévision euclidienne , et on a 4 racine évidente , alors x-4=0 Donc => x=4 ... ( 0=<x=<196 )
C'est la seule résultat que je pense. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 19:16 Mer 31 Mar 2010, 19:16 | |
| - Dijkschneier a écrit:
Problème 1 :
Résoudre dans [0;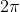 ] l'inéquation : ] l'inéquation : }}\geq%20\sqrt{2}\cos{(2x)}) . .
Voici ma solution: On a }}\geq%20\sqrt{2}\cos{(2x)}) . Premièrement, on doit poser: 2x=X. Donc }}\geq%20\sqrt{2}\cos{(X)}) . D'autre part, on sait que pour tout réel X, on a 1>=sin x>=-1. Donc 2>=sin x +1>=0. Donc le domaine de définition de cette équation est IR. Donc V2>=V(sin x =1).==>(1) Et on a 1>=cos x>=-1. Donc V2>=V2*cos x>=-V2.==(2) Et de 1 et 2, l'inéquation équivaut à }})^2\geq%20(\sqrt{2}\cos{(X)})^2) . Donc }\geq%20 2\cos^2{(X)}) . Donc }+\cos^2{(X)}+\sin{(X)}\geq%20 2\cos^2{(X)}) . Donc }+\sin{(X)}\geq%20 \cos^2{(X)}) . Donc }+\sin{(X)}\geq%20 1-\sin^2{(X)}) . Donc }+\sin{(X)}-1\geq%20 0) . On pose: t=sin x. L'inéquation devient  . Considérons le trinôme 2t^2+t-1. Le discriminent de ce trinôme est 9. (1^2-4*2*(-1)=1+8=9) Donc les solutions de l'équation 2t^2+t-1=0 sont les suivants: (pour diminuer les lignes de solutions)  et  . On factorise ce trinôme comme suit 2t^2+t-1=2(t+1)(t-1/2). Soit 2t^2+t-1=(t+1)(2t-1). On s'est arrété à  . Donc (2t-1)\geq%20 0) . Donc }+1)(2\sin{(X)}-1)\geq%20 0) . Donc, en divisant par }+1) car il est positif d'après 1 }-1\geq%20 0) . Donc }\geq%20 1) . Donc }\geq%20 \frac{1}{2}) . Résolvons cette équation }=\frac{1}{2}) . On a }=\frac{1}{2}) . Et on sait que  . Donc }) . Donc X=Pi/6 +2kPi ou X=Pi-Pi/6 +2kPi. Donc X=Pi/6 +2kPi ou X=5Pi/6 +2kPi. Et puisque X appartient à l'intervalle [0;2Pi]. Donc 0=<X=<2Pi. Donc 0=<Pi/6 +2kPi=<2Pi ou 0=<5Pi/6 +2kPi=<2Pi. Donc 0=<1/6 +2k=<2 ou 0=<5/6 +2k =<2. Donc -1/6=<2k=<2-1/6 ou -5/6=<2k=<2-5/6. Donc -1/6=<2k=<11/6 ou -5/6=<2k=<7/6. Donc -1/12=<k=<11/12 ou -5/12=<k=<7/12. Donc k=0 ou k=0. On remplace k par sa valeur dans l'expression X=Pi/6 +2kPi. Pour k=0, on trouve X=Pi/6. On remplace k par sa valeur dans l'expression X=5Pi/6 +2kPi. Pour k=0, on trouve X=5Pi/6. Donc les deux solution dans [0;2Pi] sont Pi/6 et 5Pi/6. Pour que }\geq%20 \frac{1}{2}) il faut que X appartient à l'intervalle [Pi/6;5Pi/6]. Donc Pi/6=<X=<5Pi/6. Donc Pi/6=<2x=<5Pi/6. Donc Pi/12=<x=<5Pi/12. Et finalement les solution de l'équation de départ est S=[Pi/12;5Pi/12]. Sauf faute de frappe. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 19:18 Mer 31 Mar 2010, 19:18 | |
| - M.Marjani a écrit:
- Bonne idée nmo
mais il ya une petite faute que tu viens de faire :
^2+\frac{(y-1)^2}{y^2}=3)
Il faudrait faire (y-2)² à la place de y² ( voir au dénominateur )
+ dans la prochaine étape t'as fais (y-1)²=y²-2x+1
S'il est juste une éxplication , car tu sais plus que moi ce que t'as fait  Bonne remarque, il fallait poser x=y+1. Merci pour la réponse. C'est édité.
Dernière édition par nmo le Jeu 01 Avr 2010, 17:52, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 19:28 Mer 31 Mar 2010, 19:28 | |
| - mizmaz a écrit:
- M.Marjani a écrit:
- Donc calculez-moi :

Bonne chance. - Spoiler:
Sauf erreur. 
Au plaisir ! J'ai une autre methode du collège, la voici: On a (1-\frac{1}{9})(1-\frac{1}{16})...(1-\frac{1}{625})) . Donc (1-\frac{1}{3^2})(1-\frac{1}{4^2})...(1-\frac{1}{25^2})) . Donc (1+\frac{1}{2})(1-\frac{1}{3})(1+\frac{1}{3})...(1-\frac{1}{25})(1+\frac{1}{25})) . Donc (1-\frac{1}{3})...(1-\frac{1}{25})*(1+\frac{1}{2})(1+\frac{1}{3})...(1+\frac{1}{25})) . Donc  . Donc  . Donc  . Donc  . | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 22:07 Mer 31 Mar 2010, 22:07 | |
| A vous de poser  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mer 31 Mar 2010, 23:17 Mer 31 Mar 2010, 23:17 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 19:04 Jeu 01 Avr 2010, 19:04 | |
| - Sylphaen a écrit:
- Dijkschneier a écrit:
- Deux autres, tant qu'on y est :
Problème 2 :
Soit ABC un triangle. a,b et c sont ses longueurs de côté, et alpha, bêta et gamma ses angles respectifs.
Montrez que :  . . On utilise la formule de Alkashi pour trouver que :
 Je ne pense pas, voici ma methode: Avant de commencer, pour que cela soit juste, il faut que  soit juxtaposée au côté de longueur a,  soit juxtaposée au côté de longueur b, 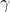 soit juxtaposée au côté de longueur c. Avec AB=c et AC=b et BC=a. Soit H le projeté orthogonal de A sur [BC]. On a dans le triangle AHB  . Donc  . Donc  . Et on a dans le triangle AHC  . Donc  . Donc  . D'autre part, on a 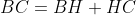 . Donc  .==>(1) De même  .==>(2) De même  .==>(3) Pour démontrer l'égalité proposée, on développe le côté droit: On a (\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1)=a*\cos{\alpha}+a*\cos{\beta}+a*\cos{\gamma}-a+b*\cos{\alpha}+b*\cos{\beta}+b*\cos{\gamma}-b+c*\cos{\alpha}+c*\cos{\beta}+c*\cos{\gamma}-c) . Donc (\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1)=a*\cos{\alpha}+b*\cos{\beta}+c*\cos{\gamma}+c*\cos{\beta}+b*\cos{\gamma}-a+c*\cos{\alpha}+a*\cos{\gamma}-b+a*\cos{\beta}+b*\cos{\alpha}-c) . Donc (\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1)=a*\cos{\alpha}+b*\cos{\beta}+c*\cos{\gamma}+a-a+b-b+c-c) . Donc (\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1)=a*\cos{\alpha}+b*\cos{\beta}+c*\cos{\gamma}) . CQFD. P.S: C'est le dernier exercice du cours de la trigonométrie. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 19:16 Jeu 01 Avr 2010, 19:16 | |
| - Calculus a écrit:
- Solve in iR:
8=x+V(14+Vx) - M.Marjani a écrit:
- On peut utiliser la dévision euclidienne , et on a 4 racine évidente , alors x-4=0 Donc => x=4 ... ( 0=<x=<196 )
C'est la seule résultat que je pense. Tu as commis une faute, le domaine de définition est [0;8]. On a 8=x+V(14+Vx). Donc 8-x=V(14+Vx). Donc (8-x)^2=[V(14+Vx)]^2. Donc 64-16x+x^2=14+Vx. Donc 64-16x+x^2=14+2-2+Vx. Donc 64-16x+x^2=16+Vx -2. Donc 16(4-x)+x^2-16+2-Vx=0. Donc 16(2-Vx)(2+Vx)+(x-4)(x+4)+(2-Vx)=0. Donc (2-Vx)[16(2+Vx)+1]+(x-V2)(x+V2)(x+4)=0. Donc (2-Vx)[16(2+Vx)+1+(x+V2)(x+4)]=0. Donc (2-Vx)[(2+Vx)(16+x+4)+1]=0. Donc 2-Vx=0 ou (2+Vx)(16+x+4)+1=0. On voit clairement que (2+Vx)(16+x+4)+1 ne peut jamais valoir 0. Donc 2-Vx=0. Donc 2=Vx. Donc x=4. Donc S={4}. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
