| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 20:18 Jeu 01 Avr 2010, 20:18 | |
| - nmo a écrit:
- Calculus a écrit:
- Solve in iR:
8=x+V(14+Vx) - M.Marjani a écrit:
- On peut utiliser la dévision euclidienne , et on a 4 racine évidente , alors x-4=0 Donc => x=4 ... ( 0=<x=<196 )
C'est la seule résultat que je pense. Tu as commis une faute, le domaine de définition est [0;8].
On a 8=x+V(14+Vx).
Donc 8-x=V(14+Vx).
Donc (8-x)^2=[V(14+Vx)]^2.
Donc 64-16x+x^2=14+Vx.
Donc 64-16x+x^2=14+2-2+Vx.
Donc 64-16x+x^2=16+Vx -2.
Donc 16(4-x)+x^2-16+2-Vx=0.
Donc 16(2-Vx)(2+Vx)+(x-4)(x+4)+(2-Vx)=0.
Donc (2-Vx)[16(2+Vx)+1]+(x-V2)(x+V2)(x+4)=0.
Donc (2-Vx)[16(2+Vx)+1+(x+V2)(x+4)]=0.
Donc (2-Vx)[(2+Vx)(16+x+4)+1]=0.
Donc 2-Vx=0 ou (2+Vx)(16+x+4)+1=0.
On voit clairement que (2+Vx)(16+x+4)+1 ne peut jamais valoir 0.
Donc 2-Vx=0.
Donc 2=Vx.
Donc x=4.
Donc S={4}. Nous pouvons également considérer la fonction f telle que : =x+\sqrt{14+\sqrt{x}}) . Nous avons donc  . Étudions maintenant les variations de f sur son domaine de définition : \in%20D_{f}^{2}\setminus%20x%3Ey\Rightarrow%20\sqrt{x}%3E\sqrt{y}\Rightarrow%2014+\sqrt{x}%3E14+\sqrt{y}\Rightarrow%20\sqrt{14+\sqrt{x}}%3E\sqrt{14+\sqrt{y}}\Rightarrow%20x+\sqrt{14+\sqrt{x}}%3Ey+\sqrt{14+\sqrt{y}}\Rightarrow%20f(x)%3Ef(y)) Et donc f est strictement croissante sur son domaine de définition. Delà nous pouvons affirmer que pour toute équation de la forme suivante : =m\setminus%20m\in%20IR) , il n'existe qu'une seule ou aucune solution. Remarquons donc que 4 est une solution évidente de l'équation =8) et affirmons que c'est la seule et unique.  Finalement,  . Au plaisir !  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 22:22 Jeu 01 Avr 2010, 22:22 | |
| [quote="nmo"] - Calculus a écrit:
- Solve in iR:
8=x+V(14+Vx) - M.Marjani a écrit:
- On peut utiliser la dévision euclidienne , et on a 4 racine évidente , alors x-4=0 Donc => x=4 ... ( 0=<x=<196 )
C'est la seule résultat que je pense. Tu as commis une faute, le domaine de définition est [0;8]. quote] oO, comment t'as eu [0,8] ? bon prend V2=V(V(V(x))) <=> x=16>V2 ! | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 22:29 Jeu 01 Avr 2010, 22:29 | |
| - nmo a écrit:
- Calculus a écrit:
- Solve in iR:
8=x+V(14+Vx) - M.Marjani a écrit:
- On peut utiliser la dévision euclidienne , et on a 4 racine évidente , alors x-4=0 Donc => x=4 ... ( 0=<x=<196 )
C'est la seule résultat que je pense. Tu as commis une faute, le domaine de définition est [0;8].
quote]
oO, comment t'as eu [0,8] ? bon prend V2=V(V(V(x))) <=> x=16>V2 ! Il a eu [0,8] en posant  Et donc puisque :  Alors :  (*) Et puisque nous avons une racine carrée écrite de la sorte : 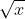 Alors :  (**) De (*) et (**) nous déduisons que :  Au plaisir !  | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 01 Avr 2010, 22:40 Jeu 01 Avr 2010, 22:40 | |
| Excusez le double-post. Tiens, on peut même aller plus loin et dire que puisque  Alors  Au plaisir ! | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 02 Avr 2010, 10:29 Ven 02 Avr 2010, 10:29 | |
| - Sylphaen a écrit:
- Voici un exo pour vous :
MQ:
 - M.Marjani a écrit:
- Sinon , on peut remarquer que :
1/2•3/4•5/6• ... •99/100 < 1/10
Il suffit donc de la prouver.
----------------------------------------------------------------------------
Posons : A = 1/2•3/4•5/6• ... •99/100. et B = 2/3•4/5•6/7• ... •98/99.
2/3 > 1/2, 4/5 > 3/4, ..., 98/99 > 97/98, 1 > 99/100.
à partir de ce dérnier on a : A < B. Donc : AB = 1/100 (1) ( en simplifiant en utilisant l'observation .. )
Alors : A2 < AB < 1/100, et on se retourne plus géneral :
1/2•3/4•5/6• ... •(2n-1)/2n < 1/(2n), (2)
A(n) = 1/2•3/4•5/6• ... •(2n-1)/2n,
B(n) = 2/3•4/5•6/7• ... •(2n-2)/(2n-1).
A(n) < 1/(3n+1). (3)
ce qui donne : (3') A(n) < 1/(3n),
-------------------------------------------------------------
Et on a A(1) = 1/2 = 1/(3•1+1).
ce qui est faux avec 2
Car : A(2) = 1/2•3/4 = 3/8 < 1/7 = 1/(3•2+1),
Faisant le carré :
9/64 < 1/7,pour 7•9 = 63 < 64
Posons : n=k
(4) A(k) < 1/(3k+1).
Et on prouve que n=k+1
(5) A(k+1) < 1/(3(k+1)+1) = 1/(3k+4).
et parceque : A(k+1) = A(k)•(2k+1)/(2k+2), (4)
Il parait clairement que : (6) A(k+1) < (2k+1)/(2k+2)•1/(3k+1).
---------------------------------------------------------------------------
Et mtn on fait le carré du coté droit :
[(2k+1)/(2k+2)•1/(3k+1)]2 = (2k+1)2 / ((2k+2)2(3k+1))
= (2k+1)2 / (12k3 + 28k2 + 20k + 4)
= (2k+1)2 / [(12k3 + 28k2 + 19k + 4) + k]
= (2k+1)2 / [(2k+1)2(3k+4) + k]
< (2k+1)2 / [(2k+1)2(3k+4)]
= 1 / (3k+4),
Qui est exactement le coté droit de (5) et qui prouve (6)
Enfin , on peut finir et trouver clairement le résultat. Je n'arrive pas à comprendre ta methode genérale,donc je réponds: Posons d'abord: A=1/2*3/4*5/6*...*9999/10000 et B=2/3*4/5*6/7*... *9998/9999. On sait que 4>3 et 16>15 et ... et 99960004>99960003 . Donc 2*2>3*1 et 4*4>3*5 et ... et 9998*9998>9999*9997. Donc 2/3>1/2 et 4/5>3/4 et ... et 9998/9999>9999/10000 et 1>9999/10000. Donc 1/2*3/4*5/6*...*9999/10000<2/3*4/5*6/7*... *9998/9999. Donc A<B. Donc A*A<B*A. Donc A^2<1/2*3/4*5/6*...*9999/10000*2/3*4/5*6/7*... *9998/9999*1. Donc A^2<1/10000. Donc A^2<(1/100)^2. Donc A<1/100. Donc 1/2*3/4*5/6*...*9999/10000<1/100. CQFD. Sauf faute de calcul.
Dernière édition par nmo le Lun 05 Avr 2010, 11:09, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 02 Avr 2010, 11:41 Ven 02 Avr 2010, 11:41 | |
| Les problèmes proposés:
1/Montrez que le produits de quatres nombres entiers consécutifs augmenté de 1 est un carré parfait.
2/p et q sont des entiers successifs.
Montrez que p^2+q^2+(pq)^2 est un carré parfait.
Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 02 Avr 2010, 13:54 Ven 02 Avr 2010, 13:54 | |
| 1/ Soit n un entier arbitraire, et soit A le produit de quatre nombres entiers consécutifs augmenté de 1. A peut être noté (n+2)(n+3)+1) , et donc, (n+2)(n+3)+1=n^4+6n^3+11n^2+6n+1=(n^2+3n+1)^2) . 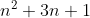 est entier, par construction de n, et de fait, ^2) est un carré parfait. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 02 Avr 2010, 14:01 Ven 02 Avr 2010, 14:01 | |
| 2/ Soit p un entier arbitraire. q est le successeur de p, et par conséquent, 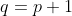 . Par suite, ^2%20=%20p^2%20+%20(p+1)^2%20+%20(p(p+1))^2%20=%20p^4+2p^3+3p^2+2p+1) . Laborieusement, la factorisation de ce polynôme peut être trouvée, et est ^2) .  étant entier, par construction de p, il s'ensuit que A est un carré parfait. | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 02 Avr 2010, 14:07 Ven 02 Avr 2010, 14:07 | |
| 2/ par symetrie des roles , on peut prendre q=p+1 ^2%20=%20p^2%20+%20(p+1)^2%20+p^2(p+1)^2%20=%20p^4+2p^3%20+%203p^2+2p+1=(p^2-p+1)^2) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 03 Avr 2010, 18:40 Sam 03 Avr 2010, 18:40 | |
| Que Dijkschneier poste un nouveau exercice.
Ses réponses sont justes. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 04 Avr 2010, 20:16 Dim 04 Avr 2010, 20:16 | |
| RE  - nmo a écrit:
- Sylphaen a écrit:
- Voici un exo pour vous :
MQ:
 - M.Marjani a écrit:
- Sinon , on peut remarquer que :
1/2•3/4•5/6• ... •99/100 < 1/10
Il suffit donc de la prouver.
----------------------------------------------------------------------------
Posons : A = 1/2•3/4•5/6• ... •99/100. et B = 2/3•4/5•6/7• ... •98/99.
2/3 > 1/2, 4/5 > 3/4, ..., 98/99 > 97/98, 1 > 99/100.
à partir de ce dérnier on a : A < B. Donc : AB = 1/100 (1) ( en simplifiant en utilisant l'observation .. )
Alors : A2 < AB < 1/100, et on se retourne plus géneral :
1/2•3/4•5/6• ... •(2n-1)/2n < 1/(2n), (2)
A(n) = 1/2•3/4•5/6• ... •(2n-1)/2n,
B(n) = 2/3•4/5•6/7• ... •(2n-2)/(2n-1).
A(n) < 1/(3n+1). (3)
ce qui donne : (3') A(n) < 1/(3n),
-------------------------------------------------------------
Et on a A(1) = 1/2 = 1/(3•1+1).
ce qui est faux avec 2
Car : A(2) = 1/2•3/4 = 3/8 < 1/7 = 1/(3•2+1),
Faisant le carré :
9/64 < 1/7,pour 7•9 = 63 < 64
Posons : n=k
(4) A(k) < 1/(3k+1).
Et on prouve que n=k+1
(5) A(k+1) < 1/(3(k+1)+1) = 1/(3k+4).
et parceque : A(k+1) = A(k)•(2k+1)/(2k+2), (4)
Il parait clairement que : (6) A(k+1) < (2k+1)/(2k+2)•1/(3k+1).
---------------------------------------------------------------------------
Et mtn on fait le carré du coté droit :
[(2k+1)/(2k+2)•1/(3k+1)]2 = (2k+1)2 / ((2k+2)2(3k+1))
= (2k+1)2 / (12k3 + 28k2 + 20k + 4)
= (2k+1)2 / [(12k3 + 28k2 + 19k + 4) + k]
= (2k+1)2 / [(2k+1)2(3k+4) + k]
< (2k+1)2 / [(2k+1)2(3k+4)]
= 1 / (3k+4),
Qui est exactement le coté droit de (5) et qui prouve (6)
Enfin , on peut finir et trouver clairement le résultat. Je n'arrive pas à comprendre ta methode genérale.. L'idée c'est prouvé que : 1/2•3/4•5/6• ... •99/100 < 1/10 Quand t-il sera prouvé on peut facilement trouvé une autre fois l'inégalité demandé. (j'ai fais trois methode la deuxiéme était trés facile, mais celle-çi est la plus compliqué éxcuse. ^^') A vous Dijckacheiner. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 05 Avr 2010, 11:15 Lun 05 Avr 2010, 11:15 | |
| - Sylphaen a écrit:
- Voici un exo pour vous :
MQ:
 J'ajoute celui-ci: Montrez que  . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 10 Avr 2010, 18:37 Sam 10 Avr 2010, 18:37 | |
| Je réponds moi-même:
Posons d'abord: A=1/2*3/4*5/6*...*9999/10000 et B=2/3*4/5*6/7*... *9998/9999.
Donc 2A=3/4*5/6*...*9999/10000 et B=2/3*4/5*6/7*... *9998/9999.
On sait que 9>8 et 25>24 et ... et 99980001>99980000.
Donc 3*3>4*2 et 5*5>6*4 et ... et 9999*9999>9998*10000.
Donc 3/4>2/3 et 5/6>4/5 et ... et 9999/10000>9998/9999.
Donc 3/4*5/6*...*9999/10000>2/3*4/5*6/7*... *9998/9999.
Donc 2A>B.
Donc 2A*A>B*A.
Donc 2A^2>1/2*3/4*5/6*...*9999/10000*2/3*4/5*6/7*... *9998/9999*1.
Donc 2A^2>1/10000.
Donc 2A^2>(1/100)^2.
Donc AV2>1/100.
Donc A>1/100V2.
Donc 1/2*3/4*5/6*...*9999/10000>1/100V2.
CQFD.
Sauf faute de calcul. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 10 Avr 2010, 18:44 Sam 10 Avr 2010, 18:44 | |
| Je vous proposes les deux exercices suivants:
Le premier exercice:
Soient a, b, et c trois réels positifs.
Montrez que (bc+1)/a +(ab+1)/c +(ac+1)/b>=6.
Le deuxième exercice:
Soient D et D' deux droites du plan tel qu'ils se coupent en A.
On pose deux points E et F tels qu'ils n'appartiennent ni à (D), ni à (D').
Expliquer comment on peut déterminer M de (D) et N de (D') pour que le quadrilatère EFMN soit un paralléllipipède.
Bonne chance.
Dernière édition par nmo le Dim 11 Avr 2010, 12:25, édité 1 fois | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 10 Avr 2010, 19:00 Sam 10 Avr 2010, 19:00 | |
| - nmo a écrit:
- Je vous proposes les deux exercices suivants:
Le premier exercice:
Soient a, b, et c trois réels.
Montrez que (bc+1)/a +(ab+1)/c +(ac+1)/b>=6.
Bonne chance. Salut, Par l'inégalité arithmético-géométrique, nous avons : - Spoiler:
Et donc l'inégalité est correcte. Sauf erreur. Au plaisir ! 
Dernière édition par mizmaz le Sam 10 Avr 2010, 19:38, édité 1 fois | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 10 Avr 2010, 19:38 Sam 10 Avr 2010, 19:38 | |
| - nmo a écrit:
Le deuxième exercice:
Soient D et D' deux droites du plan tel qu'ils se coupent en A.
On pose deux points E et F tels qu'ils n'appartiennent ni à (D), ni à (D').
Expliquer comment on peut déterminer M de (D) et N de (D') pour que le quadrilatère EFMN soit un paralléllipipède.
Bonne chance. Nous pouvons aisément trouver l'angle formé par ) et ) à l'aide d'un rapporteur, nommons-le  . De même pour l'angle formé par ) et ) , nommons-le  . Nous avons clairement  et  puisque //(EF)) . Nous avons également 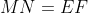 . Nommons l'angle formé par ) et ) : 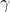 . Utilisons la règle (Si quelqu'un connait son nom, qu'il me le dise s'il vous plait) qui dit que : }{MM'}=\frac{Sin(\beta%20)}{AM}=\frac{Sin(\alpha%20)}{AM'}) pour trouver 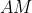 et  , et le tour est joué.  Sauf erreur. J'ai, bien sûr, considéré (EF) et (D) sécantes, ainsi que (EF) et (D'). Le cas de (EF)//(D) et celui de (EF)//(D') étant faciles à traiter. Au plaisir !  Edit : Je m'en suis rendu compte trop tard. En fait,  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 11 Avr 2010, 11:41 Dim 11 Avr 2010, 11:41 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 11 Avr 2010, 11:44 Dim 11 Avr 2010, 11:44 | |
| - mizmaz a écrit:
- nmo a écrit:
- Je vous proposes les deux exercices suivants:
Le premier exercice:
Soient a, b, et c trois réels.
Montrez que (bc+1)/a +(ab+1)/c +(ac+1)/b>=6.
Bonne chance. Salut,
Par l'inégalité arithmético-géométrique, nous avons :
- Spoiler:
Et donc l'inégalité est correcte.
Sauf erreur.
Au plaisir !  Peux-tu m'ecrire le cas général de cette inégalité pour pouvoir tester est-ce qu'elle est juste ou fausse. Je réponds sans théorème plus tard. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 11 Avr 2010, 11:48 Dim 11 Avr 2010, 11:48 | |
| - nmo a écrit:
- mizmaz a écrit:
- nmo a écrit:
- Je vous proposes les deux exercices suivants:
Le premier exercice:
Soient a, b, et c trois réels.
Montrez que (bc+1)/a +(ab+1)/c +(ac+1)/b>=6.
Bonne chance. Salut,
Par l'inégalité arithmético-géométrique, nous avons :
- Spoiler:
Et donc l'inégalité est correcte.
Sauf erreur.
Au plaisir !  Peux-tu m'ecrire le cas général de cette inégalité pour pouvoir tester est-ce qu'elle est juste ou fausse.
Je réponds sans théorème plus tard. Finalement, a,b et c doivent être strictement positifs. Sinon, a=b=c=-1 serait un joli contre exemple. Sinon, pour l'inégalité, google it.  Au plaisir !  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 11 Avr 2010, 12:31 Dim 11 Avr 2010, 12:31 | |
| - mizmaz a écrit:
- nmo a écrit:
- mizmaz a écrit:
- nmo a écrit:
- Je vous proposes les deux exercices suivants:
Le premier exercice:
Soient a, b, et c trois réels.
Montrez que (bc+1)/a +(ab+1)/c +(ac+1)/b>=6.
Bonne chance. Salut,
Par l'inégalité arithmético-géométrique, nous avons :
- Spoiler:
Et donc l'inégalité est correcte.
Sauf erreur.
Au plaisir !  Peux-tu m'ecrire le cas général de cette inégalité pour pouvoir tester est-ce qu'elle est juste ou fausse.
Je réponds sans théorème plus tard. Finalement, a,b et c doivent être strictement positifs. Sinon, a=b=c=-1 serait un joli contre exemple. Sinon, pour l'inégalité, google it. 
Au plaisir !  J'ai oublié de mensionner qu'ils sont positifs. Ta solution est juste. | |
|
  | |
abdrrazak
Débutant
 Nombre de messages : 4 Nombre de messages : 4
Age : 30
Date d'inscription : 12/04/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Lun 12 Avr 2010, 23:07 Lun 12 Avr 2010, 23:07 | |
| (a-c)^2+(a-d)^2+(b-c)^2+b-d)^2>=0(car les nombres ^2sont toujours positive)
a^2-2ac+c^2 + a^2-2ad+d^2 + b^2-2bc+c^2 + b^2-2bd+d^2>=0
donc
a^2+c^2+ a^2+d^2 + b^2+c^2+ b^2+d^2 >=2(ac+ad+bc+bd
donc
2(a^2+c^2+d^2+ b^2) >=2(ac+ad+bc+bd
so
(a^2+c^2+d^2+ b^2) >=ac+ad+bc+bd
et nous savons que :(a+b)(c+d)=ac+ad+bc+bd
donc : a^2+c^2+d^2+ b^2 >=(a+b)(c+d) | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 13 Avr 2010, 10:05 Mar 13 Avr 2010, 10:05 | |
| La solution sans théorème est ainsi:
On a (x-y)^2>=0 pour tout x et y positifs.
Et (x-z)^2>=0 pour tout x et z positifs.
Et (z-y)^2>=0 pour tout z et y positifs.
Donc, en sommant (x-y)^2+(x-z)^2+(z-y)^2>=0.
Donc x^2-2xy+y^2+x^2-2xz+z^2+z^2-2zy+y^2>=0.
Donc 2x^2+2y^2+2z^2>=2xy+2xz+2zy.
Donc 2(x^2+y^2+z^2)>=2(xy+xz+zy).
Donc x^2+y^2+z^2>=xy+xz+zy.
On prend x=1/a et y=1/b et z=1/c.
Ainsi l'inégalité devient (1/a)^2+(1/b)^2+(1/c)^2>=(1/a)(1/b)+(1/b)(1/c)+(1/c)(1/a).
Donc 1/(a^2)+1/(b^2)+1/(c^2)>=1/(ab)+1/(bc)+1/(ac).
Donc, en multipliant par abc abc/(a^2)+abc/(b^2)+abc/(c^2)>=abc/(ab)+abc/(bc)+abc/(ac).
Donc bc/a+ac/b+ab/c>=c+b+a.
Donc bc/a+ac/b+ab/c+1/a+1/b+1/c>=a+b+c+1/a+1/b+1/c.
Donc (bc+1)/a+(ac+1)/b+(ab+c)/c>=a+b+c+1/a+1/b+1/c.==>(1)
D'autre part, on a (Vx-1/Vx)^2>=0 pour tout x positif.
Donc (Vx)^2-2*1/Vx*Vx+(1/Vx)^2>=0.
Donc x-2+1/x>=0.
Donc x+1/x>=2.
Avec x=a l'inégalité devient a+1/a>=2.
Avec x=b l'inégalité devient b+1/b>=2.
Avec x=c l'inégalité devient c+1/c>=2.
Donc, en sommant a+1/a+b+1/b+c+1/c>=2+2+2.
Donc a+b+c+1/a+1/b+1/c>=6.==>(2)
Et de 1 et 2, on conclut que (bc+1)/a+(ac+1)/b+(ab+c)/c>=6.
CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 13 Avr 2010, 10:22 Mar 13 Avr 2010, 10:22 | |
| Pour le deuxième problème:
Après avoir placé E et F et (D) et (D'), on procède de la manière suivante:
On dessine (L) l'image de (D) par la translation de vecteur FE.
Les droites (L) et (D') se coupent en un point, notons le N.
Lorsqu'on dessine une droite parallèle à (EF) passant par N, elle coupe (D) en un point, notons le M.
Ainsi, on doit trouver que EFMN est un paralléllippipède.
P.S: c'est la methode du professeur.
Dernière édition par nmo le Mar 13 Avr 2010, 11:27, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 13 Avr 2010, 11:03 Mar 13 Avr 2010, 11:03 | |
| Voici un exercice de défi: Soit x un réel tel que 12<a<13. Montrez que:  . Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 13 Avr 2010, 11:32 Mar 13 Avr 2010, 11:32 | |
| Je vous propose ma propre solution pour le deuxième:
Après avoir placé E et F et (D) et (D'),on procède de la manière suivante:
Soit E' et F' les images respectifs de E et F par la symétrie cetrale de centre A.
La droite (EF') coupe (D') en N.
La droite (E'F) coupe (D) en M.
Ainsi, on doit trouver que EFMN est un paralléllippipède.
J'attends vos reclamations constructives. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
