Préparations aux olympiades de tronc commun (2009-2010)

nmo a écrit:

Je vous propose ma propre solution pour le deuxième:
Après avoir placé E et F et (D) et (D'),on procède de la manière suivante:
Soit E' et F' les images respectifs de E et F par la symétrie cetrale de centre A.
La droite (EF') coupe (D') en N.
La droite (E'F) coupe (D) en M.
Ainsi, on doit trouver que EFMN est un paralléllippipède.
J'attends vos reclamations constructives.

Pourquoi ça ?

nmo a écrit:

Voici un exercice de défi:
Soit x un réel tel que 12<a<13.
Montrez que: .
Bonne chance.

Nous avons d'une part :

Et d'autre part :

D'où le résultat.

Pour aller encore plus loin, montrez que :

Au plaisir !

mizmaz a écrit:

Pour aller encore plus loin, montrez que :
[img]http://latex.codecogs.com/gif.latex?\forall%20a\in%20[12;13]%20/%20\bigg|\sqrt{a}-\frac{\sqrt{12}+\sqrt{13}}{2}\bigg|%3C\frac{1}{14}[/img]
Au plaisir !

Les accolades n'apparaissent pas en latex, pour rectifier:

Citation :

Pour aller encore plus loin, montrez que :

Au plaisir !

nmo a écrit:

mizmaz a écrit:

Pour aller encore plus loin, montrez que :
[img]http://latex.codecogs.com/gif.latex?\forall%20a\in%20[12;13]%20/%20\bigg|\sqrt{a}-\frac{\sqrt{12}+\sqrt{13}}{2}\bigg|%3C\frac{1}{14}[/img]
Au plaisir !

Les accolades n'apparaissent pas en latex, pour rectifier:

Citation :

Pour aller encore plus loin, montrez que :

Au plaisir !

Merci bien. ^^
J'ai rectifié.

O trouve facilement que, comme a fait mizmaz:

Et d'autre part:
On a .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Finalement .
CQFD.

Exact !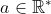

Sachant que , calculez sans trouver directement la valeur de a.
Au plaisir !

nmo a écrit:

Je réponds moi-même:
Posons t=x+1/x.
Donc t^2=x^2+2+1/x^2.
Donc t^2-2=x^2+1/x^2.
Donc (x^2+1/x^2)(x+1/x)=(t^2-2)t.
Donc x^3+x+1/x+1/x^3=t^3-2t.
Donc x^3+t+1/x^3=t^3-2t.
Donc x^3+1/x^3=t^3-3t.
Donc 18=t^3-3t.
Soit en résumé t^3-3t-18=0.
On remarque que 3 est solution évidente.
On factorise avec 3 pour obtenir (t-3)(t^2+3t+6)=0.
Donc t-3=0 ou t^2+3t+6=0.
Pour t-3=0 on obtient t=3.
Pour t^2+3t+6=0 c'est impossible car son discriminent est négatif
(3^2-4*6=9-24=-13).
D'autre part on a x+1/x=3.
Donc (x+1/x)^2=3^2.
Donc x^2+2+1/x^2=9.
Donc x^2+1/x^2=7.
Donc (x^2+1/x^2)^2=7^2.
Donc x^4+2+1/x^4=49.
Finalement x^4+1/x^4=47.

C'est la réponse.

SALUT
je vous propose cet exo
comparer

et
Bonne chance!

houssam110 a écrit:

SALUT
je vous propose cet exo
comparer

et
Bonne chance!

Posons 1,99999996=a et 1,99999995=b.
On a .
Donc .
Donc .
Donc .
De même .
D'autre part, on a .
Donc .
Donc .
Donc .
Il est clair que 1,99999996>1,99999995>1.
Donc a>b>1.
Donc ab>a>1.
Donc ab>1.
Donc 0>1-ab.
Et 1+a^2>0 et 1+b^2>0 et a-b>0.
Donc .
Donc .
Donc .

Autre exo
P(x)=x²-x-k
Q(x)=3x²+kx+m
calculer k+m si P(x) et Q(x) admettent les memes racines!
BOnne chance

houssam110 a écrit:

Autre exo
P(x)=x²-x-k
Q(x)=3x²+kx+m=0
calculer k+m si P(x) et Q(x) admettent les memes racines!
BOnne chance

Est-ce qu'on a P(x)=x²-x-k et Q(x)=3x²+kx+m et Q(x)=0.
Donc 3x²+kx+m=0?
Ou bien il s'agit d'une faute de frappe.

faute de frappe
c édité

La reponse est ainsi:
Soient a et b les racines des deux polynômes.
Donc, on peut écrire:
P(x)=(x-a)(x-b).
Q(x)=3(x-a)(x-b).
On a 3x²+kx+m=3(x-a)(x-b).
Donc 3x²+kx+m=3(x^2-xa-xb+ab).
Donc 3x²+kx+m=3x^2-3xa-3xb+3ab.
Donc 3x²+kx+m=3x^2-3x(a+b)+3ab.
Donc k=-3(a+b) et m=3ab.
Et on a P(x)=(x-a)(x-b).
Donc x²-x-k=x^2-xa-xb+ab.
Donc x²-x-k=x^2-x(a+b)+ab.
Donc a+b=1 et k=-ab.
On a trouvé que k=-3(a+b) et a+b=1.
Donc k=-3.
Donc -ab=-3.
Donc ab=3.
Maintenant, on a k+m=-3+3*3.
Donc k+m=-3+9.
Donc k+m=6.

Slt ;
On peut écrire Q(x) sous forme de : 3(x-Alpha)(x-Beta) ; P(x)(x-Alpha)(x-Beta) vu qu'ils addmetent les mémes racines.
Donc : Q(x)/P(x)=3 => Q(x)=3P(x) => 3x²+kx+m=3x²-3x-3k
=> k=-3 , m=-3k=9 => K+m=6
CQFD ^^

Mon problème proposé est le suivant:
Résolvez en IR l'équation suivante:
sin x - cos x =V2.
Bonne chance.
P.S: un exercice très facile.

Voici une facile réponse aussi ))

On a: Sinx-Cosx=V2 => -2Sinx.Cosx=1 => Sinx=-1/2cosx (1)
On remplace (1) dans la premiére equation, on trouve que : -1/2cosx-Cosx=V2 = > (-1-2cos²x-2V2Cosx) / 2cosx=0
=> -(1+V2Cosx)² / 2Cosx =0
=> Cosx=-V2/2=-Cos(Pi-Pi/4) Ou Cosx=0
=> S={Pi/2+KPi,-3Pi/4+2Kpi,3Pi/4+2Kpi}

Je propose le probléme si-dessous:
Résolvez en IR l'équation suivante:
x^5+2x^4+4x^3+8x²+16x+32=0
Bonne chance.

M.Marjani a écrit:

Je propose le probléme si-dessous:
Résolvez en IR l'équation suivante:
x^5+2x^4+4x^3+8x²+16x+32=0
Bonne chance.

Nous avons :

-2 est donc une solution évidente. Faisons une division euclidienne :

Et donc, puisque et ,
Sauf erreur.
Au plaisir !

salut naplhitl,
voila je te propose une simple soluc:

on a a²+d²>=2ad;a²+c²>=2ac;b²+c²>=2bc;b²+d²>=2bd
alors:2(a²+b²+c²+d²)>=2(ad+ac+bc+bd)=2(a+b)(c+d)
d'ou la conclusion est..
et bien sur sans aucune faute.

mizmaz a écrit:

M.Marjani a écrit:

Je propose le probléme si-dessous:
Résolvez en IR l'équation suivante:
x^5+2x^4+4x^3+8x²+16x+32=0
Bonne chance.

Nous avons :

-2 est donc une solution évidente. Faisons une division euclidienne :

Et donc, puisque et ,
Sauf erreur.
Au plaisir !

Sympa ! à vous de poster.

Pour mon exercice, il s'agit de remarquer que:
On a .
Donc .
Donc .
Donc .
Et puisque .
Il vient que .
Donc .
Donc .
Donc .
On conclut que résoudre en IR l'équation proposé n'est autre que résoudre le système:
.
Par addition des lignes, on trouve .
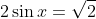Donc .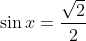
Et par la suite .
Le tableau des rapports usuels affirme que .
D'ou finalement .
P.S: ta réponse de M.Marjani est fausse.
Tu n'as qu'à remplacer par ce que tu as trouvé.
Amicalement.

Le problème courant est:
Résolvez en IR le système suivant:
.
Bonne chance.

nmo a écrit:

Le problème courant est:
Résolvez en IR le système suivant:
.
Bonne chance.

Nous avons dans un premier temps :

Nous avons
Et donc
Gardons cela d'un côté et appelons le (1).
Nous avons dans un second temps :

De (1) et du système du début, déduisons que :

Du système déduisons que :

Nommons cela (2).
Nous avons donc finalement de (1), de (2) et du système :

x,y et z sont donc les racines du polynôme P tel que :

1 étant une racine évidente, faisons une division euclidienne :

Et donc l'ensemble des solutions au système du début est :

Sauf erreur.
Au plaisir !

Bsr;
On a: x^3+y^3+z^3-3xyz=(x+y+z)(x²+y²+z²-(xy+xz+yz)) => xyz=-2
(x+y+z)²-2(xy+yz+zx)=6 => xy+yz+zx=-1 => x²y+zx²+xyz=-a
=> x²(y+z)+x-2=0 => x²(x-2)+x-2=0 => P(x)=x²-2x²+x-2=0
On a : 2 est une racines évidente. Donc prenons x=2.
Remplacant dans x+y+z=2 => y+z=0 => y=-z => 2z²=2 => z=1 Ou z=-1.
=> S={(2,1,-1);(1,2,-1);(1,-1,2);(-1,2,1);(-1,1,2);(2,-1,1)}

nmo a écrit:

P.S: ta réponse de M.Marjani est fausse.
Tu n'as qu'à remplacer par ce que tu as trouvé.
Amicalement.

Slt nmo;
Okey man
Pour l'equation, n'est pas fausse,mais il faut annuler -3Pi/4+2kpi et Pi/2 +2kpi ( car il ya la différence entre faux et résultat faux ).
Bonne chance.