Préparations aux olympiades de tronc commun (2009-2010)

[quote="mizmaz"]

nmo a écrit:

:O t'es été plus vite que moi.

[quote="M.Marjani"]

mizmaz a écrit:

nmo a écrit:

:O t'es été plus vite que moi.

Une heure entre les deux posts. :-°
Donc bon.

[quote="mizmaz"]

M.Marjani a écrit:

mizmaz a écrit:

nmo a écrit:

:O t'es été plus vite que moi.

Une heure entre les deux posts. :-°
Donc bon.

J'y vais pour manger xD
Good man, j'attend votre Exo

[quote="M.Marjani"]

mizmaz a écrit:

M.Marjani a écrit:

mizmaz a écrit:

nmo a écrit:

:O t'es été plus vite que moi.

Une heure entre les deux posts. :-°
Donc bon.

J'y vais pour manger xD
Good man, j'attend votre Exo

Soient a, b et c réels. Sachant que 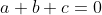et que , calculez
Au plaisir !

C fait je le copié donc

REE

M.Marjani a écrit:

Premiérement on a : (a+b+c)^4=(a²+b²+c²+2(ab+bc+ac))(a²+b²+c²+2(ab+bc+ac))
=> ab+bc+ac=-2003/2 (1)
Aussi elle donne : (a²+b²+c²)²=2003² => a^4+b^4+c^4+2(a²b²+a²c²+b²c²)
Et on a : a²b²+a²c²+b²c²=-a²(a+c)-a²(a+b)-b²(a+b)=(b+c)(a+c)+(b+c)(a+b)+(a+c)(a+b)
=ab+bc+ac+c²+ac+bc=-2003/4 + c(a+c+b)=-2003/4
a^4+b^4+c^4=2003²-2(a²b²+a²c²+b²c²) => a^4+b^4+c^4=2003²+2(2003/4)=4013010.5=_ 4.01*10^6
CQFD

La méthode a l'air correcte, mais le résultat est faux.
Recommence.
Au plaisir !

[quote="mizmaz"]

M.Marjani a écrit:

Au plaisir !

Ouii, autre faute de frappe
C'est réctifier , au lieu d'écrire ab+ac+bc=-2003/2 j'ai écrais -2003/4
Cbon, c'est réctifier. Its good ?

[quote="M.Marjani"]

mizmaz a écrit:

M.Marjani a écrit:

Au plaisir !

Ouii, autre faute de frappe
C'est réctifier , au lieu d'écrire ab+ac+bc=-2003/2 j'ai écrais -2003/4
Cbon, c'est réctifier. Its good ?

Non, toujours faux.

Premiérement on a : (a+b+c)²(a²+b²+c²)=0 => ab+bc+ac=-2003/2 (1)
=> [ a²+b²+c²+2(ab+ac+bc)][a²+b²+c²]=0
=> a^4+b^4+c^4+2(a²b²+a²c²+b²c²)+[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4+2((ab+ac+bc)²-2(ab²c+ac²b+ba²c))+[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4=-2((ab+ac+bc)²-2(ab²c+ac²b+ba²c))-[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4=-2((ab+ac+bc)²-2(abc(a+b+c)))-[a²+b²+c²]*2[ab+ac+bc]=0
a+b+c=0 => a^4+b^4+c^4=-2((ab+ac+bc)²))-[a²+b²+c²]*2[ab+ac+bc]=0

=> a^4+b^4+c^4=..

M.Marjani a écrit:

Premiérement on a : (a+b+c)²(a²+b²+c²)=0 => ab+bc+ac=-2003/2 (1)
=> [ a²+b²+c²+2(ab+ac+bc)][a²+b²+c²]=0
=> a^4+b^4+c^4+2(a²b²+a²c²+b²c²)+[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4+2((ab+ac+bc)²-2(ac+ab+bc))+[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4=-2((ab+ac+bc)²-2(ab+ac+bc))-[a²+b²+c²]*2[ab+ac+bc]=0
=> a^4+b^4+c^4= -2[(2003/2)²+2003]+[2003]*2003
=> a^4+b^4+c^4=2001998.5

Si tu pouvais écrire en Latex, ce serait vraiment cool de ta part.
Sinon, le résultat est faux encore une fois. xD

[quote="mizmaz"]

M.Marjani a écrit:

Premiérement

La fatigue ma touché hier lol
Regarde si ce résultats te plais ou pas xD
a^4+b^4+c^4=2003²/2=2006004.5 ,+j'ai évité le remplacement des chiffres au premiér. ( Sinon tu avais qlq chose anormale dans l'énoncé ou bien vérifier que : )
(C'est réctifier), dsl pour le LaTeX, je vais l'utiliser prochainement

Ok voilà avec le LaTeX :

[quote="M.Marjani"]

mizmaz a écrit:

M.Marjani a écrit:

Premiérement

La fatigue ma touché hier lol
Regarde si ce résultats te plais ou pas xD
a^4+b^4+c^4=2003²/2=2006004.5 ,+j'ai évité le remplacement des chiffres au premiér. ( Sinon tu avais qlq chose anormale dans l'énoncé ou bien vérifier que : )
(C'est réctifier), dsl pour le LaTeX, je vais l'utiliser prochainement

Anormal ?
Sinon, oui, c'est le bon résultat.
A toi.

Ok. Cool.
------------------------------------------------------------------------



------------------------------------------------------------------------

Bonne chance.

M.Marjani a écrit:

Ok. Cool.
------------------------------------------------------------------------



------------------------------------------------------------------------

Bonne chance.

Par symétrie des rôles, nous pouvons supposer sans crainte que :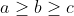

Et que :

Utilisons l'inégalité du réordonnement pour affirmer que est inférieur à toute autre combinaison avec et
Donc :

D'autre part, on par l'inégalité arithmético-géométrique :

En sommant (1) et (2), nous obtenons l'inégalité espérée.
Sauf erreur.
Au plaisir !

mizmaz a écrit:

M.Marjani a écrit:

Ok. Cool.
------------------------------------------------------------------------



------------------------------------------------------------------------

Bonne chance.

Par symétrie des rôle, nous pouvons supposer sans crainte que :

Et que :

Utilisons l'inégalité du réordonnement pour affirmer que est inférieur à toute autre combinaison avec et
Donc :

D'autre part, on par l'inégalité arithmético-géométrique :

En sommant (1) et (2), nous obtenons l'inégalité espérée.
Sauf erreur.
Au plaisir !

Nice man Nice.
A vous

Soient a, b, c les longueurs des côtés d'un triangle.
Montrez que :

Bjr ^^
Vu que c'est homogene poson a+b+c=1

on a alr l'inégalité équivaut a :
a/(1-a) +b/(1-b) + c /(1-c) < 2
supposons aussi que a>=b>=c
il suffit alors de montrer que a<1/2

on a : a < b+c
2a<a+b+c
2a<1
a < 1/2
ce qui conclu ^^

darkpseudo a écrit:

Bjr ^^
Vu que c'est homogene poson a+b+c=1

on a alr l'inégalité équivaut a :
a/(1-a) +b/(1-b) + c /(1-c) < 2
supposons aussi que a>=b>=c
il suffit alors de montrer que a<1/2

on a : a < b+c
2a<a+b+c
2a<1
a < 1/2
ce qui conclu ^^

C'est correct.
A toi.

Une assez facile , a,b,c >0 Prouvez que :
a^3+b^3+c^3 >=a^2b+b^2c+c^a>=3abc

darkpseudo a écrit:

Une assez facile , a,b,c >0 Prouvez que :
a^3+b^3+c^3 >=a^2b+b^2c+c^a>=3abc

Par l'inégalité du réordonnement, nous avons clairement si nous posons :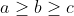

Sauf erreur.
Au plaisir !

Oui c'est juste , On peut la démontrer sans réordonnement mais bon c'est pareil , a toi ^^

darkpseudo a écrit:

Une assez facile , a,b,c >0 Prouvez que :
a^3+b^3+c^3 >=a^2b+b^2c+c^a>=3abc

J'ai pas trouvé mieux que l'inégalité du réordonnement, on considérant que a>=b>=c, On va trouvé ce qu'on cherche.

Puis application directe d'IAG
a²b+ac²+b²c=(ab)²/b + (ac)²/a + (bc)²/c>=3abc

----------------------------------------------------------------------
[J'ajoute] On peut montrer aussi que a^3+b^3+c^3>=3abc :

Aprés deux factorisations on trouve que :
a^3+b^3+c^3=(a+b+c)(a²+b²+c²-(ab+ac+bc))+3abc
Ce qui veut dire bien que : a^3+b^3+c^3>=3abc
Egalité si a=b=c.

Xd si tu montre les deux ta déja montrer que a^3+b^3+c^3>=3abc
Moi ce que j'ai di c'est que suffit de tout mettre d'un coter et de factoriser ^^