Préparations aux olympiades de tronc commun (2009-2010)

posons :
on a :
alors :

pour n=0 on aura :

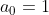pour n=1 on aura :

pour n=2 on a:

......
......
.......
pour n=9 on a:

ainsi on a 10inconnus avec 10 équations...alors on peut les calculer....mais bon....ça peut prendre des semaines et des semaines je crois qu'on aura besoin d'un programme associé à ce genre de calcul;)

oué c cke jé trouvé aussi
mais on peut dire ki system qui contientt 10 des an de 0juka 9
avec 10 conditions différentes cela peu ns mener a une unike solution pour a_n 0=<n=<9

@majdouline : ton raisonnement ne prouve pas vraiment l'existence : le fait de poser est équivalent à dire que P(x) est un polynôme, or, c'est justement le but de la question.

Dijkschneier a écrit:

@majdouline : ton raisonnement ne prouve pas vraiment l'existence : le fait de poser est équivalent à dire que P(x) est un polynôme, or, c'est justement le but de la question.

on suppose que P(x) est un polynôme....n'oublions pas que depuis l'énoncé de l'exo....P(x) existe......
on a trouvé 10 équations à dix inconnus ....donc on est capable de les calculer...sauf que cela peut durer longtemps..où bien on peut utiliser les problèmes associes à ce genre de calculs...si on les calcule ....ça va rassurer l'existence...et répondra à l'unicité ou la diversité ....
et par contre...si on trouve pas des solutions à ce système====>implique que P(x) n'existe pas.....
P.S.depuis l'énoncé de l'exo...P(x) existe...notre but est de prouver l'unicité..... ou de trouver une contradiction===>P(x) n'existe pas......il ne s'agit pas de prouver l'existence qui est déjà une donnée depuis l'énoncé de l'exo

majdouline a écrit:

P.S.depuis l'énoncé de l'exo...P(x) existe...notre but est de prouver l'unicité..... ou de trouver une contradiction===>P(x) n'existe pas......il ne s'agit pas de prouver l'existence qui est déjà une donnée depuis l'énoncé de l'exo

Plus explicitement, et d'une manière tout à fait indépendante d'un quelque problème, voilà le fond de ma question :
Prouver qu'il existe un polynôme de degré 9, tel que pour tout entier , .
Prouver que ce polynôme est unique.

Bjr :

Pour tout systéme composé d'autant d'inconnu que d'équations et dont toute les equations sont de premié degré il existe une et une seul solution :
Dans notre cas on a 9 équations et 9 inconnu ( a1;a2;a3....;a9)
toute les equations sont de premié degré !! Donc l'unicité de P(x) est pourvé !!

Pour cela nommons l'expression G : P(x) est un polynome
cette expression équivaut au fait que le systéme a une seul solution ,
puisque ce systéme a une seul solution , donc P(x) est un polynome !!
Sauf erreur

darkpseudo a écrit:

Pour cela nommons l'expression G : P(x) est un polynome
cette expression inclu le fait que le systéme a une seul solution ,
puisque ce systéme a une seul solution , donc P(x) est un polynome !!
Sauf erreur

En clair, tu dis que :
est vraie ;
F est vraie ;
Donc, G est vraie ;
où G est l'expression : "P(x) est un polynôme", et F l'expression : "Le système a une seule solution".
Vrai ?

Non au fait je voulais dire équivaut dsl !! Faute d'innatention c'est corrigé

darkpseudo a écrit:

Non au fait je voulais dire équivaut dsl !! Faute d'innatention c'est corrigé

Pourquoi est vraie ?

tentation de raisonnement .....
pour le système admet des solutions=>P(x) un polynôme qui existe ..peut être expliquée par le fait que :
supposons donc qu'on a trouvé les a_i qui satisfont les conditions des 10 équations ....ainsi
pour tout 0≤n≤9 on a :

ainsi pour prouver l'existence se P(n) il suffit de prendre :

pour la deuxième question ....
puisque le polynôme existe alors le système admet des solutions ....et puisque les équations de notre système sont du premiers degré alors P(n) est unique

Dijkschneier a écrit:

darkpseudo a écrit:

Non au fait je voulais dire équivaut dsl !! Faute d'innatention c'est corrigé

Pourquoi est vraie ?

Au fait c'est évident , quelque soit les solution de ce probléme il sera possible de les écrire sous forme de polynome du 9iéme degré on aura ainsi :

a1n + a2n^2 + a3n^4... + a9n^9 = P(n)

Et puisque pour tout n compris entre 0 et 9

a1n + a2n^2 + a3n^4... + a9n^9 = n/(n+1)

on aura :
P(n) = n/(n+1)
CQFD
Sauf erreur !

darkpseudo a écrit:

Dijkschneier a écrit:

darkpseudo a écrit:

Non au fait je voulais dire équivaut dsl !! Faute d'innatention c'est corrigé

Pourquoi est vraie ?

Au fait c'est évident , quelque soit les solution de ce probléme il sera possible de les écrire sous forme de polynome du 9iéme degré on aura ainsi :

a1n + a2n^2 + a3n^4... + a9n^9 = P(n)

Et puisque pour tout n compris entre 0 et 9

a1n + a2n^2 + a3n^4... + a9n^9 = n/(n+1)

on aura :
P(n) = n/(n+1)
CQFD
Sauf erreur !

ton problème c'est que tu suppose que P(n) est un polynôme or c'est ce qu'on chercher à démontrer...
P.S.j'attends encore des remarques sur mon raisonnement.....

AU FAITE nn je n'est pas supposé que P(n) existe :
j'ai posé P(n) = sigma ain^i

et puisqu'on j'ai déja prouvé auparavant que le systéme a une et une seul solution , donc il y aura un et un seul polynome P(n) qui remplira la condition !!
Ton raisonnement ressemble au mien juste que tu a commencer par ce dont moi j'ai fini , c'est correct je trouve !! Enfin passons a autre chose veuillez poster un probléme svp

darkpseudo a écrit:

AU FAITE nn je n'est pas supposé que P(n) existe :
j'ai posé P(n) = sigma ain^i

et puisqu'on j'ai déja prouvé auparavant que le systéme a une et une seul solution , donc il y aura un et un seul polynome P(n) qui remplira la condition !!
Ton raisonnement ressemble au mien juste que tu a commencer par ce dont moi j'ai fini , c'est correct je trouve !! Enfin passons a autre chose veuillez poster un probléme svp

le fait de poser P(n) = sigma ai.n^i c'est de supposer que P(n) est un polynôme==>alors il existe ...implicitement tu as supposé l'existence... .....

Au fait c'est évident , quelque soit les solution de ce systéme il sera possible de les écrire sous forme de polynome du 9iéme degré on aura ainsi :

a1n + a2n^2 + a3n^4... + a9n^9 = P(n)

Voila c'est ce que j'ai écri en haut , quelque soit les nombre a1,a2...,a9 , il sera possible de les écrire sous forme de polynome , et pour appuyer l'unicité de ce polynome il suffit de dire que 0 en est une racine et là on sera sûr qu'il n'y a qu'un polynome qui rempli la condition !
Je n'est pas supposé l'existence d'un polynome j'ai juste di que les nombre a1,a2...a9 appartiennent forcément a un polynome de neuviéme degré ^^'

majdouline a écrit:

tentation de raisonnement .....
pour le système admet des solutions=>P(x) un polynôme qui existe ..peut être expliquée par le fait que :
supposons donc qu'on a trouvé les a_i qui satisfont les conditions des 10 équations ....ainsi
pour tout 0≤n≤9 on a :

ainsi pour prouver l'existence se P(n) il suffit de prendre :

pour la deuxième question ....
puisque le polynôme existe alors le système admet des solutions ....et puisque les équations de notre système sont du premiers degré alors P(n) est unique

La question de l'unicité est effectivement très facile une fois que l'existence est justifiée.
Aussi, je ne comprends pas pourquoi tu as affirmé que :

Dijkschneier a écrit:

majdouline a écrit:

tentation de raisonnement .....
pour le système admet des solutions=>P(x) un polynôme qui existe ..peut être expliquée par le fait que :
supposons donc qu'on a trouvé les a_i qui satisfont les conditions des 10 équations ....ainsi
pour tout 0≤n≤9 on a :

ainsi pour prouver l'existence se P(n) il suffit de prendre :

pour la deuxième question ....
puisque le polynôme existe alors le système admet des solutions ....et puisque les équations de notre système sont du premiers degré alors P(n) est unique

La question de l'unicité est effectivement très facile une fois que l'existence est justifiée.
Aussi, je ne comprends pas pourquoi tu as affirmé que :

en fait...je l'ai pas affirmé et g dis une fois on trouve des solution au système....on l'affirme...veuillez lire ce qui est en rouge en haut.....

j'ajoute :on doit trouver des solutions au système...sinon P(n) n'existe pas .....(absurde:supposons que P(n) existe===>le système n'admet pas de solutions contradiction)
alors on doit forcèrent trouver les solution au système ce qui affirme que : pour tout 0≤n≤9 on a :
ce qui reste toujours c'est le problème de résoudre le système.....comme j'ai dit il faut du temps ou un programme associé

majdouline a écrit:

j'ajoute :on doit trouver des solutions au système...sinon P(n) n'existe pas .....(absurde:supposons que P(n) existe===>le système n'admet pas de solutions contradiction)
alors on doit forcèrent trouver les solution au système ce qui affirme que : pour tout 0≤n≤9 on a :
ce qui reste toujours c'est le problème de résoudre le système.....comme j'ai dit il faut du temps ou un programme associé

En clair, tu dis que :
L'existence des solutions du système est une condition suffisante à l'existence du polynôme.
Ou encore par contraposée :

Pourquoi ?

justement oué...et g pas mal expliqué ça
si on trouve des solutions au système ;alors :
pour tout 0≤n≤9 on a :

alors il suffit de prendre :

ainsi :le système admet des solutions=>P(x) un polynôme qui existe
alors en faisant la contraposée

j'espere que j'ai pu expliquer ce que je veux dire....
sauf erreur....

c'est quoi un polynôme??

.

Dijkschneier a écrit:

.

Toujours avec les polyômes, voici mes problèmes:
1/On considère le polynôme P tel que:
P(x)=(x-a)(x-b)/(c-a)(c-b) + (x-b)(x-c)/(a-b)(a-c) + (x-c)(x-a)/(b-c)(b-a).
Et a, b, et c sont des nombres différent deux à deux.
Montrez que pour tout x de IR P(x)=1.
**Premièrement, il faut calculer P(a), P(b), et P(c).
2/**Montrez qu'il existe un et un seul polynôme du second degré tel que pour m, n, et p des nombres connues:
P(1)=m, P(2)=n, et P(3)=p.
**Trouvez ce polynome tel que:
#m=n=p=2500.
#m=3, n=6, et p=9.
#m=1, n=4, et p=9.
Bonne chance.
P.S: Je suis faible en ce qui concerne la démonstration de l'unicité et l'éxitude d'un polynome, pouvez-vous m'expliquer?
(C'est la et la seule raison pour laquelle je n'est pas participé à la résolution du dernier problème.)
Merci d'avance.

Je vous donne l'indice suivant qui va vous aider à faire le premier exercice:
Que peut-on dire d'un polynome d'un degré n ayant (n+1) racines?