Préparations aux olympiades de tronc commun (2009-2010)

Ok, merci pour la remarque (j'ai pensé que: AB=a !). b²+c²-a²/2=2AI² <=> AI²-a²/4=bc*Cos(A)

Le réciproque:



Les deux médianes orthogonaux => (AI)_|_(BM).
Pytaghore dans ABG: c²=[AG]²+[BG]²=(4/9)AI²+(4/9)BJ² <=> c²=(4/9)[AI²+BJ²]
Avec: AI²=b²/2 + c²/2 -a²/4 , BJ²=a²/2 +c²/2 - b²/4 (theoréme de la médiane).
c²=(4/9)(b²/2 +c²/2 -a²/4+a²/2 + c²/2 -b²4)
= 2(b²+2c²+a²)/9 -(a²+b²)/9
= (2(b² + 2c² + a²) -a²-b²)/9
= (b²+a²+4c²)/9
=> 9c²=b²+a²+4c²
=> 5c²=b²+a²

Bonne chance.

M.Marjani a écrit:

Le réciproque:

Les deux médianes orthogonaux => (AI)_|_(BM).
Pytaghore dans ABG: c²=[(2/3)AG]²+[(2/3)BG]²=(4/9)AI²+(4/9)BJ² <=> c²=(4/9)[AI²+BJ²]
Avec: AI²=b²/2 + c²/2 -a²/4 , BJ²=a²/2 +c²/2 - b²/4 (theoréme de la médiane).
c²=(4/9)(b²/2 +c²/2 -a²/4+a²/2 + c²/2 -b²4)
= 2(b²+2c²+a²)/9 -(a²+b²)/9
= (2(b² + 2c² + a²) -a²-b²)/9
= (b²+a²+4c²)/9
=> 9c²=b²+a²+4c²
=> 5c²=b²+a²
Bonne chance.

En fait c²=AG²+BG².
Ce qui ramène à c²=[(2/3)AI]²+[(2/3)BM]².
Et ensuite à c²=(4/9)[AI²+BJ²].
(Une petite faute d'inattention)
Ta solution est juste, à toi de proposer le prochain exercice.
Je vais poster une autre réponse se basant sur l'analyse.

Oui, j'ai voullu montrer l'étape d'ou je viens de (4/9)AI mais..

Exercise proposé:

Si x,y,z>0 tels que: x+y+z=xyz alors montrez que:


Bonne chance.

Avant de cotinuer le jeu:
Une solution analytique pour l'exercice que j'ai présenté:
Choisissons un repère porté par (AB) et la hauteur assossiée.
On note , , et .
Soit A' le milieu de (BC) et B' le milieu de (AC).
On a .
Donc .
Donc .
Et on a .
Donc .
Donc .
De même .
Ces vecteurs sont orthogonaux si, et seulement si .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .==>(*)
Calculons maintenant les distances AC, AB, et BC.
Posons encore a=BC, b=CA, et c=BA.
On a .
Donc .
Donc .
Donc .
De même .
Et .
En remplaçant dans *, on trouve .
Donc .
CQFD.

M.Marjani a écrit:

Exercise proposé:
Si x,y,z>0 tels que: x+y+z=xyz alors montrez que:

Bonne chance.

Bon, voici la réponse:
Pour tout a, b, et c de IR, on a , et .
D'où, en sommant .
Donc .
Donc .
Donc .
Prenons: , , et .
Alors .
Donc .
Donc .
Donc .
Donc .
Donc .
CQFD.

Exercice proposé:
Calculez A,
Sachant que .
Bonne chance.

Bravo, mais...

nmo a écrit:

Prenons: , etc..

Qui vous assure que xy, xz et yz sont supérieurs à 1 ?

Les deux solutions de l'équation quadratique



sont



et

.

La suite



de terme général



est une suite de Fibonacci.











Par conséquent,

pour l'inégo du M.Marjani :

avec un petit changement de variable , on suppose :

d'ou
et :


c b1 vu que : 1+ tg²(alpha)=1/cos²(alpha)
et
alors : -cos(alpha+beta)=cos(gamma)


alors il fallait prouver que :


puisque on a : tg(alpha)tg(beta)-1=cos(gamma)/cos(alpha)cos(beta)

alors

CQFD !

Salam, pour nmo et Dijkasheiner je suis désolé de vous dire que le latex que vous avez utiliser est illisible en ce moment. Priére de le réecrire une autre fois.

Pour Master: Oui, vous pouvez supposez a=tg(Alpha).. mais on peut pas dire forcément que Alpha,..£ ]0,Pi/2[. on peut supposer cette derniere mais.. Sinon l'idée est joli.

Je vous partagerai ma solution prochainement. Merci.

slt M.Marjani , just notons qu'alors alpha,beta,gamma , peuvent etre considérés comme les angles d'un triangle aigu !! ce qui donne
alpha+beta+gamma=pi et alpha,beta,gamma£]0,pi/2[

Dijkschneier a écrit:

Bravo, mais...

nmo a écrit:

Prenons: , etc..

Qui vous assure que xy, xz et yz sont supérieurs à 1 ?

On a x+y>0 selon les données.
Donc x+y+z>z.
Donc xyz>z.
Donc xy>1.
De même pour les autres.

Bien.

Dijkschneier a écrit:

Les deux solutions de l'équation quadratique sont et .
La suite de terme général est une suite de Fibonacci.










Par conséquent,

Cela me parait juste.
Rapelle toi de:

Dijkschneier a écrit:

Donc, et

Ainsi tu peux faire une petite substition pour trouver le résultat.
A toi de proposer un nouvel exercice pour ne pas laisser ce jeu bloqué.

Quelle substitution, spécialement ? Ici, il ne s'agit pas de la suite de Fibonacci au sens strict, mais au sens généralisé, et en l'occurrence, de la suite de Lucas. Les nombres de Lucas et de Fibonacci sont bien reliées entre eux, avec la formule : L(n) = 2 F(n-1) + F(n), où L(n) et F(n) désignent respectivement le énième nombre de Lucas et de Fermat, mais il m'eut étonné que c'est de cela dont vous souhaitez parler ?

Dijkschneier a écrit:

Quelle substitution, spécialement ? Ici, il ne s'agit pas de la suite de Fibonacci au sens strict, mais au sens généralisé, et en l'occurrence, de la suite de Lucas. Les nombres de Lucas et de Fibonacci sont bien reliées entre elles, avec la formule : L(n) = 2 F(n-1) + F(n), où L(n) et F(n) désignent respectivement le énième nombre de Lucas et de Fermat, mais il m'eut étonné que c'est de cela dont vous souhaitez parlez ?

Pour être franc, je ne sais pas tout cela, ce que je veux dire est:
Si x est un réel vérifiant x^2-x-1=0.
Alors x^10=55x+34.==>(*)
Les deux solutions de l'équation quadratique sont et .
Remarque que .
Tu remplace en *, et tu trouves que A=123.
C'est ça mon point de vue.

Je vous comprends, nmo. Bien pensé.
Problème :
Trouvez toutes les paires d'entiers relatifs (x,y) telles que :
x^3 = y^3 + 2y^2 + 1

Dijkschneier a écrit:

Problème :
Trouvez toutes les paires d'entiers relatifs (x,y) telles que :
x^3 = y^3 + 2y^2 + 1

On a .
Donc .
Donc .
Donc .
Donc
Il s'agit d'une équation à résoudre dans l'ensemble des entiers relatifs.
On se ramène aux systèmes suivants:
*Le premier cas:
On a .
Donc .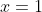
Remplaçons dans l'équation proposées:
On a .
Donc .
Donc .
Donc .
Donc ou .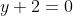
Donc 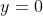ou .
D'où
Le second cas:
On a .
Donc .
Donc .
Donc
Donc .
L'équation n'admet pas de solution relative car son discriminent est strictement négatif.
Le troisième cas:
On a .
Donc .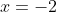
Remplaçons dans l'équation proposées:
On a
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc .
Donc 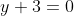ou .
L'équation n'admet pas de solution relative car son discriminent est strictement négatif.
Donc .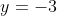
D'où .
Le quatrième cas:
On a .
Même démarche utilisé en second cas.
Même résultat aussi.
Le cinquième cas:
On a .
Donc .
Et on revient au premier cas.
Le sixième cas:
On a .
Même démarche utilisé en second cas.
Même résultat aussi.
Le septième cas:
On a .
Donc .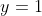
Même démarche utilisé en second cas.
Même résultat aussi.
Le huitième cas:
On a .
Même démarche utilisé en second cas.
Même résultat aussi.
Conclusion:
Les paires d'entiers relatifs (x,y) sont l'intersection de 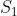et de .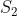
C'est à dire .
Sauf erreur bien sur.
Remarque:
Plusieurs factorisation sont enviseageables:
1/.
2/.
C'est factorisation nous mènes vers plusieurs cas, surtout la première.

Je vous propose un problème de geométrie analytique:
(D) et (D') sont deux droites strictement parallèles.
A est un point qui appartient à (D), A' est un point de (D').
Pour tout point M de (D), on définit le point M' de (D') tel que .
Montrez que la droite (MM') passe par un point fixe.
Bonne chance.

Je propose encore:
Déterminez toutes les fonctions définies de vers et qui réalisent .
Bonne chance.
P.S: J'ai édité mes derniers posts, dorénavant ils sont lisibles.
Une question: Quand le Latex serait réparé, ou bien il ne serait jamais réparé?

L'inégalité est vérifiée pour tout triplet d'entiers (k,m,n) ? Admettons que oui.
Soit f une fonction qui vérifie les conditions de l'énoncé.
Fixant k=0 et m=1, l'inégalité implique que f(0)[2-f(n)]>=1, ce qui implique que 2-f(n)>=1 étant donné que la fonction est à valeurs dans IN. On en déduit que 1>=f(n) pour tout n de IN.
Fixant m=n=1, l'inégalité implique que f(k)[2-f(1)]>=1, c'est-à-dire que f(k)>=1 (pour tout k de IN) suivant le même argument que précédemment.
Par conséquent, f(n)=1 pour tout n de IN.
Inversement, la fonction constante f(n)=1 vérifie les conditions de l'énoncé.

Dijkschneier a écrit:

L'inégalité est vérifiée pour tout triplet d'entiers (k,m,n) ? Admettons que oui.
Soit f une fonction qui vérifie les conditions de l'énoncé.
Fixant k=0 et m=1, l'inégalité implique que f(0)[2-f(n)]>=1, ce qui implique que 2-f(n)>=1 étant donné que la fonction est à valeurs dans IN. On en déduit que 1>=f(n) pour tout n de IN.
Fixant m=n=1, l'inégalité implique que f(k)[2-f(1)]>=1, c'est-à-dire que f(k)>=1 (pour tout k de IN) suivant le même argument que précédemment.
Par conséquent, f(n)=1 pour tout n de IN.
Inversement, la fonction constante f(n)=1 vérifie les conditions de l'énoncé.

Il faut que tu expliques cela.

Bonjour,
Soit f une fonction vérifiant l'énoncé.
* Posant mnk=0, de l'énigalité: [f(0)][2-f(0)]>=1, donc f(0)=1.
* Posant k=mn=0, donc 2f(0)-[f(k)]²>=1 puisqu'il est définie de |N vers |N implique que: 0=<f(k)=<1 pour tout k de |N.
* Si f(k)=0, on aura f(kn)+f(km)>=1, et en fixant k=m=n on trouve que f(k²)>=1/2, cela implique que f(k²)=1/2, par conséquent m=k=n => [f(k²)][2-f(k)]>=1 d'ou: f(k²)>=1. Et çela montre la fausté de f(k²)=1/2, d'ou f(k)=0 est fausse. Donc il réste f(k)=1.
* réciproquement, f est la seule fonction qui vérifie l'énoncé, celui-là est constante.
---------------------------------------------------------------------------
J'ai changé de methode pour enléver le chapeau pour dijksheiner qui la inspirer

nmo a écrit:

Dijkschneier a écrit:

f(0)[2-f(n)]>=1, ce qui implique que 2-f(n)>=1 étant donné que la fonction est à valeurs dans IN. On en déduit que 1>=f(n) pour tout n de IN.
f(k)[2-f(1)]>=1, c'est-à-dire que f(k)>=1 (pour tout k de IN) suivant le même argument que précédemment.

Il faut que tu expliques cela.

Par l'absurde, supposons que f(n)>1. f étant à valeurs dans IN, cela équivaut à f(n)>=2. Alors, 2-f(n)<=0 et f(0) >= 2. De fait, f(0)(2-f(n)) <= 0. Contradiction.
De même pour l'autre.