| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 01 Juin 2010, 15:10 Mar 01 Juin 2010, 15:10 | |
| Pour abc=<1/2:
J'ai montré que: abc<V3/3, de l'égalité j'ai remarqué que: 1/2 est la racine évidente la plus approcher à V3/3. Donc: abc-1/2=0 <=> abc=1/2.
Sinon donne ton contre exemple. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 12:04 Jeu 03 Juin 2010, 12:04 | |
| Je propose un nouvel exercice.
Problème :
Déterminer les mesures des angles d'un triangle rectangle ABC tel que M est le milieu de l'hypoténuse [BC] et AM² = AB.AC | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 14:45 Jeu 03 Juin 2010, 14:45 | |
| Bonjour;
Supposons que: , ABC triangle rectangle en A.
On sait que: AM²=AB*AC et: AM=BC/2 <=> BC²/4=AB*AC
D'ou BC/4AC=AB/BC (1)
D'autre part: AM²=(vec)AC.AB+(1/4)AB² (علاقة المتوسط) et: AM²=AB*AC
<=> (vec)AC.AB+(1/4)BC²=AB*BC
=> AC²-(vec)BC.AC=AB*AC-(1/4)BC²
Donc: (vec)BC.AC=AC²-AB*AC+(1/4)BC²
Et d'aprés (1) On a: (vec)BC.AC=-3AC²+(1/4)BC² (A)
Et on sait que: (vec)BC.AC=BC*AC*Cos(c) (B)
De (A) et (B) on résulte que: -3AC²+(1/4)BC²=BC*AC*Cos(c)
=> Cos(x)=(-3AC)/BC*AC + BC²/(BC*AC) = -3AC/BC+ BC/AC (3)
On sait que Cos(c)=AC/BC, Et d'aprés (3) on trouve que:
Cos(c)=-3Cos(c)+1/Cos(c) => Cos²(c)=1/4
(c) angle dans un triangle donc: (c)£[0,Pi/2]
Donc: Cos(c)=1/2=Cos(Pi/3)
On résoud l'equation dans [(0,Pi/2] on trouve que: (c)=Pi/3
D'ou: (a)=Pi/2 et: (c)=Pi/3 et (b)=Pi/6
CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 17:30 Jeu 03 Juin 2010, 17:30 | |
| - M.Marjani a écrit:
- Bonjour;
Supposons que: , ABC triangle rectangle en A.
On sait que: AM²=AB*AC et: AM=BC/2 <=> BC²/4=AB*AC
D'ou BC/4AC=AB/BC (1)
D'autre part: AM²=(vec)AC.AB+(1/4)AB² (علاقة المتوسط) et: AM²=AB*AC
<=> (vec)AC.AB+(1/4)BC²=AB*BC
=> AC²-(vec)BC.AC=AB*AC-(1/4)BC²
Donc: (vec)BC.AC=AC²-AB*AC+(1/4)BC²
Et d'aprés (1) On a: (vec)BC.AC=-3AC²+(1/4)BC² (A)
Et on sait que: (vec)BC.AC=BC*AC*Cos(c) (B)
De (A) et (B) on résulte que: -3AC²+(1/4)BC²=BC*AC*Cos(c)
=> Cos(x)=(-3AC)/BC*AC + BC²/(BC*AC) = -3AC/BC+ BC/AC (3)
On sait que Cos(c)=AC/BC, Et d'aprés (3) on trouve que:
Cos(c)=-3Cos(c)+1/Cos(c) => Cos²(c)=1/4
(c) angle dans un triangle donc: (c)£[0,Pi/2]
Donc: Cos(c)=1/2=Cos(Pi/3)
On résoud l'equation dans [(0,Pi/2] on trouve que: (c)=Pi/3
D'ou: (a)=Pi/2 et: (c)=Pi/3 et (b)=Pi/6
CQFD. Tu veux dire que -3AC²+(1/4)BC²=AC²-AB*AC+(1/4)BC². Donc 4AC²=AC*AB. Donc 4AC=AB. Ce qui n'est pas présent dans les données. Ainsi ta solution est fausse. (Tu n'as pas bien remplacé en utilisant (1)). Réessaye. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 17:31 Jeu 03 Juin 2010, 17:31 | |
| - Dijkschneier a écrit:
- Je propose un nouvel exercice.
Problème :
Déterminer les mesures des angles d'un triangle rectangle ABC tel que M est le milieu de l'hypoténuse [BC] et AM² = AB.AC Voici ma solution: La mesure de l'angle ABC est b, celle de l'angle ACB est c. L'hypoténuse est [BC], donc le triangle ABC est rectangle en A. Donc la mesure de l'angle BAC est  . Selon la loi des sinus, on a  . Donc  . Donc  . On a M le milieu de [BC]. Donc AM=BM=CM=(1/2)BC. On a  . Donc ^2=AB.AC) . Donc  . Donc  . Donc  . Donc  . Donc  . On sait que  . Donc  . Remplaçons donc: On a  . Donc }.\sin{b}=\frac{1}{4}) . Donc  . Les angles ABC et ACB sont aigus, donc leurs rapports triangulaires sont positifs. (on peut passer à la racine et au carré sans problèmes) Donc ^2) . Donc .\sin^2{b}=\frac{1}{16}) . Donc  . Donc  . Donc  . Résolvons cette équation: Posons  . Donc notre équation équivaut à  . Cette équation a pour discriminent:  . Et  . Donc ^2-4*16*1) . Donc  . Donc  . Donc  . Cette équation a pour racines x1 et x2. Et  et  . Donc -8\sqrt{3}}{2*16}) et +8\sqrt{3}}{2*16}) . Donc  et  . Donc  et  . (les deux solutions sont positives) Donc  ou  . Donc  ou  . Donc  ou  . Donc ^2}{8}) ou ^2}{8}) . Donc ^2}{8}}) ou ^2}{8}}) . Donc  ou  . Donc  ou  . On sait que  et  . Donc  ou  . Donc  ou  . Donc  ou }) . Donc  ou  . Donc  ou  . Si  . Alors  . Donc  . Si  . Alors  . Donc  . Sauf erreur. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 17:52 Jeu 03 Juin 2010, 17:52 | |
| - nmo a écrit:
Tu veux dire que -3AC²+(1/4)BC²=AC²-AB*AC+(1/4)BC².
Donc 4AC²=AC*AB.
Donc 4AC=AB.
Ce qui n'est pas présent dans les données.
Ainsi ta solution est fausse.
(Tu n'as pas bien remplacé en utilisant (1)).
Réessaye. D'aprés (1): AB=4AC , Multipliant par AC <=> AB*AC=4AC² <=> -AB*AC=-4AC². D'ou: AC²-AB*AC+(1/4)BC²=AC²-4AC²+(1/4)BC².. donc ca marche.. Je vais lire ta methode (malgré il est trés looonGue) :p (Il faut réflichir avant d'agir) | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:02 Jeu 03 Juin 2010, 18:02 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:12 Jeu 03 Juin 2010, 18:12 | |
| Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:24 Jeu 03 Juin 2010, 18:24 | |
| - M.Marjani a écrit:
- nmo a écrit:
Tu veux dire que -3AC²+(1/4)BC²=AC²-AB*AC+(1/4)BC².
Donc 4AC²=AC*AB.
Donc 4AC=AB.
Ce qui n'est pas présent dans les données.
Ainsi ta solution est fausse.
(Tu n'as pas bien remplacé en utilisant (1)).
Réessaye. D'aprés (1): AB=4AC , Multipliant par AC <=> AB*AC=4AC² <=> -AB*AC=-4AC².
D'ou: AC²-AB*AC+(1/4)BC²=AC²-4AC²+(1/4)BC².. donc ca marche..
Je vais lire ta methode (malgré il est trés looonGue) :p
(Il faut réflichir avant d'agir) Le 1 dans ta démonstration n'est pas ce 1 que tu dis. Ma démonstration est fort juste car j'ai fait BC²=BC.BC. Et j'ai remplaçé. J'attends l'avis de Dijkschneier. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:41 Jeu 03 Juin 2010, 18:41 | |
| - nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
Tu veux dire que -3AC²+(1/4)BC²=AC²-AB*AC+(1/4)BC².
Donc 4AC²=AC*AB.
Donc 4AC=AB.
Ce qui n'est pas présent dans les données.
Ainsi ta solution est fausse.
(Tu n'as pas bien remplacé en utilisant (1)).
Réessaye. D'aprés (1): AB=4AC , Multipliant par AC <=> AB*AC=4AC² <=> -AB*AC=-4AC².
D'ou: AC²-AB*AC+(1/4)BC²=AC²-4AC²+(1/4)BC².. donc ca marche..
Je vais lire ta methode (malgré il est trés looonGue) :p
(Il faut réflichir avant d'agir) Le 1 dans ta démonstration n'est pas ce 1 que tu dis.
Ma démonstration est fort juste car j'ai fait BC²=BC.BC.
Et j'ai remplaçé.
J'attends l'avis de Dijkschneier. BC/4AC=AB/BC <=> BC/BC=AB/4AC <=> 1=AB/4AC <=> AB=4AC.. C'est faux ce que t'as utilisé.. regarde la premiére étape que t'as utiliser dans la loi des sinus.. et compare là avec BC²=.. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:55 Jeu 03 Juin 2010, 18:55 | |
| salam
A propos de l'exercice précédent:
AM²=AB.AC
BC²/4 = AB.AC
1/4 = (AB/BC).(AC/BC)
1/4 = cosB.sinB
1/2= 2cosB.sinB
1/2=sin(2B)
2B= pi/6
B=pi/12 ====> C= 5pi/12
. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 18:58 Jeu 03 Juin 2010, 18:58 | |
| - nmo a écrit:
- Spoiler:
- Dijkschneier a écrit:
- Je propose un nouvel exercice.
Problème :
Déterminer les mesures des angles d'un triangle rectangle ABC tel que M est le milieu de l'hypoténuse [BC] et AM² = AB.AC Voici ma solution: La mesure de l'angle ABC est b, celle de l'angle ACB est c. L'hypoténuse est [BC], donc le triangle ABC est rectangle en A. Donc la mesure de l'angle BAC est  . Selon la loi des sinus, on a  . Donc  . Donc  . On a M le milieu de [BC]. Donc AM=BM=CM=(1/2)BC. On a  . Donc ^2=AB.AC) . Donc  . Donc  . Donc  . Donc  . Donc  . On sait que  . Donc  . Remplaçons donc: On a  . Donc }.sin{b}=frac{1}{4}) . Donc  . Les angles ABC et ACB sont aigus, donc leurs rapports triangulaires sont positifs. (on peut passer à la racine et au carré sans problèmes) Donc ^2) . Donc .sin^2{b}=frac{1}{16}) . Donc  . Donc  . Donc  . Résolvons cette équation: Posons  . Donc notre équation équivaut à  . Cette équation a pour discriminent:  . Et  . Donc ^2-4*16*1) . Donc 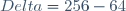 . Donc 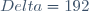 . Donc  . Cette équation a pour racines x1 et x2. Et  et  . Donc -8sqrt{3}}{2*16}) et +8sqrt{3}}{2*16}) . Donc  et  . Donc  et  . (les deux solutions sont positives) Donc  ou  . Donc  ou  . Donc  ou  . Donc ^2}{8}) ou ^2}{8}) . Donc ^2}{8}}) ou ^2}{8}}) . Donc  ou  . Donc  ou  . On sait que  et  . Donc  ou  . Donc  ou  . Donc  ou }) . Donc  ou  . Donc  ou  . Si  . Alors  . Donc  . Si  . Alors  . Donc  . Sauf erreur.
Le résultat est correct. Je n'ai pas entièrement lu ta démonstration, car sa présentation ne le permet pas. Pour tes prestations futures, veille à sauter certaines étapes qui peuvent être facilement comprises afin de gagner en concision. Cela aurait un impact certain sur ceux qui te liront alors. Mais laissez-moi vous proposer une solution différente :  Soit H le projeté orthogonal de A sur (BC). (AH) est alors une hauteur. .(2AM)%20\Leftrightarrow%20sin{\widehat{BMA}}%20=%20\frac{1}{2})  ou  . Par symétrie, choisissons  . ABM étant isocèle en M, il vient que  . Dès lors,  Finalement, puisque la situation est symétrique, la permutation entre la mesure des deux angles B et C donne une solution également valable. - M.Marjani a écrit:
- Voici ta grande faute nmo:

C'est plutot: ^2=4AB.AC)
A toi de reprendre nmo  Pas du tout. La démonstration de Nmo semble tenir debout, contrairement à la tienne. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 19:32 Jeu 03 Juin 2010, 19:32 | |
| - Dijkschneier a écrit:
- Je ne sais pas ou est l'erreur. Voilà un EX qui compte réflichir..
Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 22:01 Jeu 03 Juin 2010, 22:01 | |
| ma solution n'est -elle pas intéressante ??
je vois que aimez beaucoup les longues discussions.
. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 22:46 Jeu 03 Juin 2010, 22:46 | |
| - houssa a écrit:
- ma solution n'est -elle pas intéressante ??
je vois que aimez beaucoup les longues discussions.
. A mon avis votre solution est la meilleur Mr Houssam. Le passage du produit au Sin était sympa  Quelques identités que vous avez utiliser n'existe pas au programe TC, mais ta methode reste la plus courte et la meilleur. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 03 Juin 2010, 22:49 Jeu 03 Juin 2010, 22:49 | |
| Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 09:50 Ven 04 Juin 2010, 09:50 | |
| - M.Marjani a écrit:
- nmo a écrit:
- M.Marjani a écrit:
- nmo a écrit:
Tu veux dire que -3AC²+(1/4)BC²=AC²-AB*AC+(1/4)BC².
Donc 4AC²=AC*AB.
Donc 4AC=AB.
Ce qui n'est pas présent dans les données.
Ainsi ta solution est fausse.
(Tu n'as pas bien remplacé en utilisant (1)).
Réessaye. D'aprés (1): AB=4AC , Multipliant par AC <=> AB*AC=4AC² <=> -AB*AC=-4AC².
D'ou: AC²-AB*AC+(1/4)BC²=AC²-4AC²+(1/4)BC².. donc ca marche..
Je vais lire ta methode (malgré il est trés looonGue) :p
(Il faut réflichir avant d'agir) Le 1 dans ta démonstration n'est pas ce 1 que tu dis.
Ma démonstration est fort juste car j'ai fait BC²=BC.BC.
Et j'ai remplaçé.
J'attends l'avis de Dijkschneier. BC/4AC=AB/BC <=> BC/BC=AB/4AC <=> 1=AB/4AC <=> AB=4AC..
C'est faux ce que t'as utilisé.. regarde la premiére étape que t'as utiliser dans la loi des sinus.. et compare là avec BC²=.. Ce qui est en rouge est tellement faux. Ceci n'est pas autorisé. Amicalement. P.S: la methode de Dijkschneier est bien organisé. Quant à celle de houssa, il faut qu'il démontre ce qu'il a utilisé car nous sommes encore en tronc commun (en réalité, c'est le résumé de ce que j'ai fait). | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 11:46 Ven 04 Juin 2010, 11:46 | |
| - nmo a écrit:
- houssa a écrit:
je vois que aimez beaucoup les longues discussions.
.
Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 12:21 Ven 04 Juin 2010, 12:21 | |
| - M.Marjani a écrit:
- Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. Posons AM=x, alors BM=1-x. On a M un point du segment [AB]. Donc AM=<AB. Donc x=<1. Donc 2x=<2. Donc 2x-1=<1. Donc 0=<(2x-1)²=<1. Donc 0=<4x²-4x+1=<1. Donc 1=<4x²-4x+2=<2. Donc 1/2=<(4x²-4x+2)/2=<2/2. Donc 1/2=<2x²-2x+1=<1. Donc 1/2=<x²+x²-2x+1=<1. Donc 1/2=<x²+(1-x)²=<1. Donc 1/2=<AM²+BM²=<1.==>(1) De même, on démontre que 1/2=<PB²+PC²=<1.==>(2) Et 1/2=<RC²+RD²=<1.==>(3) Et 1/2=<AS²+SD²=<1.==>(4) En sommant ces quatres inégalités, côté par côté, on trouve 1/2+1/2+1/2+1/2=<AM²+BM²+PB²+PC²+RC²+RD²+AS²+SD²=<1+1+1+1. Donc 2=<AM²+BM²+PB²+PC²+RC²+RD²+AS²+SD²=<4.==>(*) D'autre part, on a AMR un triangle rectangle en A. Donc, selon le théorème de pytagore AM²+SA²=SM². De même, on démontre que MB²+BP²=MP². Et PC²+CR²=PR². Et QD²+DS²=QR². En remplaçant dans *, on trouve 2=<MP²+PR²+RS²+SM²=<4. CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 12:52 Ven 04 Juin 2010, 12:52 | |
| Je vous propose cet exercice: a est un réel vérifiant  . Montrez que  . Bonne chance. | |
|
  | |
master
Maître

 Nombre de messages : 298 Nombre de messages : 298
Age : 31
Localisation : Morocco-Méknés - tata
Date d'inscription : 10/01/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 13:23 Ven 04 Juin 2010, 13:23 | |
| a^5-a^3+a=a(a^4-a²+1)=2 <==> a^4-a²+1=2/a <==>
(multipliant avec a²+1) a^6= 2(a+ 1/a)-1
2(a + 1/a)-1>=4-1= 3 ==> a^6>= 3
2)
2+a^3=a^5+a <==> 2/a^3 +1 = a²+ 1/a²>= 2
2/a^3>=1 <==> a^3<=2 <==> a^6 <= 4 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 13:32 Ven 04 Juin 2010, 13:32 | |
| On peut facilement prouver que ce réel a ne peut être que positif. Dès lors,  , la première inégalité étant une application de l'IAG. Bon, master m'a devancé. Bravo. | |
|
  | |
houssa
Expert sup
 Nombre de messages : 1693 Nombre de messages : 1693
Age : 68
Date d'inscription : 17/11/2008
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Ven 04 Juin 2010, 15:14 Ven 04 Juin 2010, 15:14 | |
| pour nmo
salam
je ne sais pas exactement ce qui est autorisé dans les réponses
par exemple:
j'ai lu des passages dans des réponses comme:
5^{1/3} ......est ce au programme du tronc commun ?
d'après l'IAG ....est ce au programme du tronc commun ?
résoudre : (a^x).(b^(y-5)) = 2 ....x et y réels ....
est ce au programme du tronc commun ?
.
............................................ | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 05 Juin 2010, 01:51 Sam 05 Juin 2010, 01:51 | |
| Re à vous :p Déja on a: x>0 [le 0 ne satisfait pas l'énoncé]. Si x£]0,1[ on a: x^3>=x^5 <=> x^5-x^3=<0 <=> x^5-x^3+x<1. Absurde Si x=1: 1-1+1=1<2 absurde. D'ou x>1. Considéron a>=0 et appliquant l'AM-GM: 1(a^5-a^3+a)>=(-a^5*a^3*a)^{1/3} <=> (a^5-a^3+a)>=-a^3 <=> a^6=<4. Clair que a>1 (Si a=<1 On trouve que: a^5-a^3+a<2] .. Multipliant l'éfalité de départ par a: a^6-a^4+a²=2a <=> a^6=(a²-a)(a²+a)+2a => a^6>=a²+a+2a>=a²+2a+1>=(a+1)²>=4. D'ou: 
Dernière édition par M.Marjani le Sam 05 Juin 2010, 21:22, édité 1 fois | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 05 Juin 2010, 12:42 Sam 05 Juin 2010, 12:42 | |
| - M.Marjani a écrit:
- Exercise proposé:
ABCD est un carré dont les côtés ont pour longueur 1.
M , P , R et S sont 4 points situés respectivement sur [AB] , [BC] , [CD] et [DA].
Montrer que 2 < MP2 + PR2 + RS2 + SM2 < 4
Bonne chance. Ma methode:On a: MP²+PR²+RS²+SM²=AB²+BC²AD²+DC²-2(BP*PC+..+AS*SD)=4-2(BP*PC+..+AS*SD)<4 (1) Supposons que: AM=<DR=<BM MP²+PR²+RS²+SM²>=2(PC*RC+MB*PB+SD*DR+AM*SA)=2((1-BP)(1-DR)+(1-AM)*PB+AM*(1-SD)+SD*DR = 2(1-BP-DR+BP*DR+PB-AM*PB+AM-AM*SD+SD*DR) = 2(1+AM+SD*DR-DR+BP*DR-AM(SD+PB) = 2(1+AM-AM(PB+SD+DR(SD+BP)) = 2(1+AM+(BP+SD)(DR-AM)) > 2 D'ou: 2 < MP2 + PR2 + RS2 + SM2 < 4. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
