Exo par Exo ( en attendant le jeu d'été)

Thalès a écrit:

Il doit forcément y avoir une erreur, la question serait plutôt de minorer l'expression et non pas de déterminer la valeur minimale.

Une question de minoration n'aurait pas un intérêt ici. Il est possible de minorer cette expression avec tout réel inférieur ou égal à 1/27 : quel est l'intérêt, ensuite ? De même, on peut la majorer avec tout réel supérieur à 1 : l'intérêt ? Dans ce cas, on aurait même pas besoin de la condition (x+y+z)^3 = 32xyz.
Je crois que la question telle qu'elle a été posée par tarask est bien fondée. En revanche, 1/27 n'est pas le minimum recherché. Le maximum non plus n'est pas la valeur "1".

Ce qui m'a poussé à dire cela c'est la réponse de Tarask :

tarask a écrit:

oui master bien fait il te reste l'autre partie!!

On est censé croire que la valeur 1/27 est la valeur recherchée et que la méthode est juste, donc soit l'énoncé est faux (chose qui me semble impossible), soit Tarask n'est pas sûr de sa réponse et n'a pas la correction de l'exercice.

édité

Salut les ami(e)s! Salut Thalèse, j'espère que tu as bien ecrasé le national!
En ce qui concerne le problème, on peut toujours supposer que x+y+z=1 => xyz=1/32 car l'expression qu'on cherche a minimiser et maximiser est homogène, et après poser q=xy+yz+zx, puis maximiser et minimser q, ceci est faisable on considerant f(x)=xy+yz+zx=yz+x(y+z)= x(1-x) + 1/(32x)
f'(x)=1-2x-1/(32x²)=(1-4x)(16x²-4x-1)/32x²
on trouvera alors que que la seule solution possible pour x>=0 est 1/4 =<x=<(1+V5)/8 et que: f(1/4)>=q>=f((1+V5)/.
l'expression proposer vaut: x^4+y^4+z^4, ou encore 1-4q-2q²+1/16, soit g le fonction tels que g(q)=2q²-4q+15/16. g'(q)=4(q-1)=<0, d'où: g(f(1/4))=<g(q)=<g(f((1+V5)/)
on encore 9/128=<g(q)=<(383-165V5)/256, ce qui achève la preuve. le cas d'égalité est retirable de la demo même (2,1,1) et (3-V5;(1+V5)/2;(1+V5)/2). sauf erreur!!

Si je dois proposer un exo, j'espère qu'on me le signale le plus vite possible.

Oui voilà ta réponse est juste, tu as été plus rapide que moi =)
Bah j'ai essayé d'écraser le national comme revanche puisqu'on m'a écrasé au régional xDD

PS: Pour Dijkschneier, est-ce que tu as reçu le message que je t'ai envoyé hier?

Thalès a écrit:

soit Tarask n'est pas sûr de sa réponse et n'a pas la correction de l'exercice.

Dsl pour le retard , et bien voilà j'ai trouvé cet exo dans un fichier (en effet ça provient du Vietnam 2004) pour la réponse , j'avais fait comme "master" c'est pour ça que j'ai cru que c'était juste (dsl) et veuillez me pardonner parce que j'ai pas la correction de l'exercice !!
En tout cas de telles discussions sont toujours bénéfiques !

Oui c'est vrai c'est toujours bénéfique, d'ailleurs moi je n'avais pas fait attention au cas d'égalité impossible qui permet d'obtenir la valeur 1/27.

Bon je crois que c'est à MohE de nous proposer un exo nn?

Soit a,b et c des réels positifs tels que a+b+c=1/a+1/b+1/c. Prouver que:
1/(2a+b+c)² + 1/(2b+a+c)² + 1/(2c+a+b)² =< 3/16

P.S: je m'excuse si le problème est facile.

slt Mohe,

mais voici ma solution:

on a

et puisque l'inégalité est homogène, on peut donc supposer que a+b+c=3

alors l'inégo devient
en posant

et en utilisant la tangeante de la fonction en 1 on obtient:

ce qui conclut la démonstration
sauf erreur bien entendu...

slt , dsl pour retard , mais just je voulais poster une autre soluc pour exo du tarask ^^ :
posons
,
,
d'ou :

.
a,b,c réels racings pour l'équation suivante :
alors :
f(x)=0 , avec
d'ou on tient :

qui conduit alors a :
et ,


d'ou :
et ,
qui donne alors :

alors :

supposons u²=tv²
donc l'inégo est équivalente a :



alors b1 vus que :





alors le max détient avec la valeur t=16/15 , qui donne :

v²=15u²/16
avec a,b,c les racings d'équation suivante :

reda-t, peut-tu m'expliquer pourquoi l'inégalité est homogène?

Citation :

et en utilisant la tangeante de la fonction en 1 on obtient:

Peut-être un peu plus de détails ?

on a: ab+ac+bc=abc(a+b+c)
et : (ab+ac+bc)²>=3abc(a+b+c) d'où abc(a+b+c)>=3
on peut aussi prouver que a+b+c>=3
on a par (y+x)²>=4xy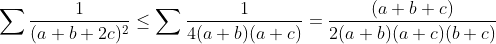



et on a :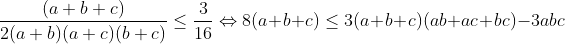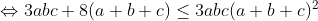



d'après les 1ér inégalités on a :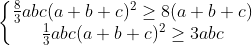



on somme est c'est fini

exo :
trouver tous les entiers positifs a,b tels que ab²+b+7 soit un diviseur de a²b+a+b .

c deja posté , en tt cas voila la soluc :

on pose S=( a²b + a + b)/(ab² + b + 7 )
on a : |bS-a|=|b²-7a|/(ab² + b + 7 )

si b>=3 : b²=7a d ou la solution est (7k²;7k)
si b=2: |2S-a|=(7a-4)/(4a + 9 ) =< 1 d ==> 7a-4=4a+9 (pour qu'il sera un entier) ==> a=13/3 absurde (a£N)
si b=1 : |N-a|=(7a-1)/(a + 8 )
donc a+8 £ {1;3;19;57}==> a£{11,49} , alors (a,b)=(11,1)ou(49,1)

si a=b=0 ==> la soluc alors est (7k,0)
d'ou la conclusion du S ...

ok poste un exo stp

Personne n'as poster je pose cette petite inégalitée assez facil :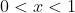


k appartient a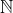
prouvez que :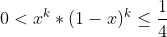





0<x^k * ( 1-x)^k =< 1/4


Sans récurrence !!

dsl darkpseudo , je ne vois r1 d'apres votre latex , si c'est possible que tu dénontre cet erreur ou tu poste autre exo pourr atthenter le jeu !!! ^^

Je sais pas pourquoi ça marche pas , tu peux soit recopier l'écriture dans un site latex , soit voir en bas j'ai éditer sans latex

bon alors permettez-moi de vous donner ma solution :



sauf erreur !

C'est juste , pourtant je comprend pas pourquoi t'as multipilier par -1 ça n'as fait que compliqué la chose ; enfin bon a toi de poster !!

Une question , je viens d'arriver du lycée ibn yasmine , on a passer un test de maths ( assez difficile vue que c'etait du début d'année ) ; moi j'ai été informé samedi soir , donc j'ai pa eu le temps de réviser , et je sais même pas a quoi sert ce test , si quelqu'un a des infos , merci !

Lol nous aussi on va passer un test le mercredi et je sait pas à quoi ça servirait

darkpseudo a écrit:

je comprend pas pourquoi t'as multiplier par -1 ça n'as fait que compliqué la chose ; enfin bon a toi de poster !!

bn c pas très compliqué , tout ce que j'ai fait c'est de rendre tous les termes en une seule partie à droite c'est tout mais bn c pas grand chose !
y a -t-il une autre méthode plus simple que celle-ci? enfin si personne ne le fait autrement!
bn voilà mon exo :


Pour ton test il semble que c'est mieux d'ouvrir un autre sujet pour ne pas gâcher le jeu

darkpseudo a écrit:

k appartient a
prouvez que :
0<x^k * ( 1-x)^k =< 1/4

C'est plutot: K>1 avec K£|N. J'avais une autre methode, elle suffit de montrer qu'elle est réalisé pour k=2.