Exo par Exo ( en attendant le jeu d'été)

SAlut ]b]l'exercicen'est pas tres difficile [/b]... et le raisonement de azzdine est correct juste il est perturbé car il n'a pas bien lu l question moi j'aai sui le meme raisonement é j'ai trouvé la solution correcte si je me rappel javé trouvé que 2^^b -1 |2^k CQFD ...

pour exo 3 ! je trouve la soluc de azzdine est vrais ! sinn je posterais ma soluc aprés !
P.S les exos postés sont a la porté pour que le tt les forumistes participerais !

Oui tout à fait d'accord master , il est très très facile de poser des exos que personne ne peut résoudre mais on veut que tout le monde participe !

master a écrit:

pour exo 3 ! je trouve la soluc de azzdine est vrais ! sinn je posterais ma soluc aprés !
P.S les exos postés sont a la porté pour que le tt les forumistes participerais , pas pour montrer vos orgeuilles ( j'indicule pas le tt ) ! un peu de modeste svp vous lonutera rien ! le jeu est créer pour apprendre et maitriser maths ! meme on trouveras des bn exos la bas !

tu vx po arreter toi cke tu fé toi .. mais jvé rien dire... t le meilleur avec des solutions copiées de mathslink pffff j'en ai marre...
PS: tu dois changer ta localisation
il vaut mieu qu'on laisse le jeu continue... é je vais plus répondre a tes messages...

dsl(...)

.

allez les gars faut agir comme des matheux nn?
copier les solutions ou pas c pas le problème , on est là pour s'entraider, je vais comme même pas autoriser de tels commentaires dans ce jeu ! veuillez supprimer vos derniers msgs !!!

suis d'acc ac master , nous somme ici pour apprendre , pas pour montrer des arrogances ! comme a fu houssame , et je m'excuse si je suis sur l'offensif ! c b1 vu que tu est trop orgeuilleux comme a dit plusieurs forumistes !

émmm je vois que tout le monde est contre moi ...
mais vous n'allez pas comprendre pourquoi j'ai réagi comme sa ... kon qq t'insulte et insulte DIEU ... je sais plus quoi faire tarask va mettre fin a cela en proposant un nouveau exercice...
BON JEU ...

dsl (...)

bn maintenant que les msgs sont passés en plein jeu je vous demande sérieusement de les supprimer s'il vouuuus plaaaaaiiiiit !!!!!!!

SALut je pense qu'il ya un probleme dans le jeu ...
j'aime beaucoup ce genre de jeu c'est pour cela je prefere qu'il continue
bon le probleme de tarask est résolu par master et par azzdine celui de mitting aussi
je vais vous proposer un nouvel exercice pour terminer le jeu et oublier ce qui s'est passé
BON !
EXERCICE PROPOSé
soit p;q;r des nombres premiers tels que
p^3=p²+q²+r²
trouver p ;q et r
si vous pensez que ce n'est pas la bonne idée vous pouvez me le demander et je supprime mon message ...
Bonne chance
A+ IMAANE

merci imanos , je m'excuse mais ....... suis po le fautif ok , pour l'exo :
p^3=p²+q²+r² ==> p²(p-1)=q²+r²
p>=q>=r
2p²>=q²+r² ===> 2p²>=p²(p-1) ==> 3>=p
d'ou p£{-3,-2,-1,0,1,2,3}
si p=0 ==> q=r=0 ==> contradiction
si p=-1,-2,-3 ==> contradiction
si p =1 ==> r=q=0 ==> contradiction
si p=2, ==> de meme méthode en déduit les solucs (0,2) ===> contra
si p=3 ac meme facon pour conclure que les solucs sont (3,3)
d'ou la conclusion de S ={3,3,3}

master a écrit:

merci imanos , je m'excuse mais ....... suis po le fautif ok , pour l'exo :
p^3=p²+q²+r² ==> p²(p-1)=q²+r²
p>=q>=r
2p²>=q²+r² ===> 2p²>=p²(p-1) ==> 3>=p
d'ou p£{-3,-2,-1,0,1,2,3}
si p=0 ==> q=r=0
si p=-1,-2,-3 ==> contradiction
si p =1 ==> r=q=0
si p=2, ==> de meme méthode en déduit les solucs (0,2)
si p=3 ac meme facon pour conclure que les solucs sont (3,3) et (-3,-3)
d'ou la conclusion de S
si j'ai commis une faute inturner svp car j'ai pas b1 calculer !

bonsoir !! d'abord il faut savoir que les nombre premier £ IN
0 n'est pas premier
1 n'est pas premier
---------------------------
on a pas le droit de supposer p>=q>=r car ce n'est pas symetrique
seule q et r qui jouent des rôles symetriques...
AMICALEMENT ...

ah oui j'ai pas b1 lu l'exo (premier) ! et pour la symetrie je crois qu'elle possible pour les équation diophantiennes !

OK s'elle est possible suppose que q>=r>=p et fait l'exercice...

je comprends po ce que tu veux dire imanos ^^ , mais selon ma modeste connaisance sur les équations diophantiennes , on peuvent supposer une symétrie de role ! sinn la seule solution je crois est (3,3,3) !

- Premiérement:
* p^3=p²+q²+r² (la somme de trois carré positives) => p>1 => q>1,r>1. (A)
* Si p=2: p²+q²+r²=8 => q²+r²=4 ==> Absurde! Donc p,q,r des premiers impaires.
* On a: p^3-p²=q²+r² => p=(q/p)²+(r/p)²+1 (1) => (q/p)²+(r/p)²=2k.
- Par (1) c'est clair que p²|q² et p²|r², et on sait que PGCD(p,q,r)=1, donc p²=q²=r², et par (A) on aura: p=q=r=3.

Deuxiéme methode:
De ce qui précede:
- (q²+r²)/p²=2k (1) => q²+r²=2kp² * Nous avons: p=1+(q²+r²)/p².
* Donc p=2k+1. Et en remplaçant le p par cette valeur dans (1), on aura:
* q²+r²=2k(2k+1)² => k=1 ==> q²+r²=18 <=> q=r=3.
* p²(p-1)=q²+r² => p²(p-1)=18 => p=3.
- D'ou S={3,3,3}.

Merçi.

pour lexo de imanos :
supposons que p et r et q sont différent de 3 alors ona :

r²+q² = 2mod(3)
donc p²(p-1)=2(mod3) ce qui est impossible donc r=3 ou q=3 ou p=3
si p=3 on obtient façilement p=q=r=3 sinon on suppose que q=3 et (p,r)=1 alors on aura :

p²(p-1)=r²+9 donc r est impaire et aussi p=3(mod4) donc il existe un k de Z tq p=4k+3
on a: r²=-9 (mod p) donc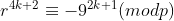
par fermat on a: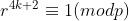
donc :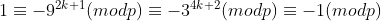

d'après fermat aussi
donc p | 2 ce qui est absurde
enfin la seule solution est p=q=r=3 ..

bjr : ^^
alors ma méthode du symetrie et aussi just puisque j'ai trouver meme soluc, et éspérons de Dieu qu'il ca sera po encore copié de mathlinks ! donc je posterais on exo :

exo proposé :
soient x,y,z des entiers strict positifs tel que 2x^x+y^y=3z^z
prouver que x=y=z
amusez-vous

BJR !
* (x,y,z)£|N*. Mq: * 2^x+y^y=3z^z <=> x=y=z.
---------------------------------------------------------------------------
* Supposant que x=/y=/z et montrant sa fausté:
On a: (x^x-z^z)+(x^x-z^z)+(y^z-z^z)=0
* Solutions envisagé: x>0,z>0,y<0, Ou bien: x<0,z<0,y>0.
Ce qui est absurde car (x,y,z)>0.
* Maintenant, supposant que x>y>z:
* On a: x>y => x^x>y^x => 2y^x+x^y<2x^x+y^y
2x^x+y^y-3z^z=0 => 2y^x+x^y-3z^z<0. Absurde !
* De méme pour x<y<z, 2y^x+y^y-3z^z>0. Absurde !
- Donc 2^x+y^y=3z^z <=> x=y=z.

Merçi.

effectivement , just on vas utiliser résonnement ac absurde !
bon , tu poste ton exo M.Marjani !

Mon exercise proposé est ainsi:

Soit (a,b,c,x,y,z) £ |R+, tel que x+y+z=1. Montrez que:
ax+by+cz+2V((xy+yz+xz)(ab+bc+ac))=<a+b+c.

Bonne chance.

premierement :

supposons x>=y>=z>=a>=b>=c
donc d'aprés réordonnement :

donc on déduit :

Salut :
malheureusement la solution présentée par master pour mon exercice est totalement fausse ... Or, celle de azzdine est bien correcte je peux bien décider c'est a tarask de parler...
A+
Imaane