| | Retour au plaisir :) |  |
|
+33Othmaann MohE Xien ali-mes einstein20 sweet-mounir M.Marjani L'enfant ayoubmath phenix darkpseudo louis supista nmo houssa anas-az_137 stylo vs calculator marouan777 mizmaz Bison_Fûté Mr.Wajih m_zeynep Fermat-X just-abdess mathslover majdouline abdellah=einstein Dijkschneier Sporovitch amazigh-tisffola tarask meryem1994 Sylphaen 37 participants |
|
| Auteur | Message |
|---|
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 10:41 Mar 16 Nov 2010, 10:41 | |
| Ah, oui ! Désolé ! C'est corrigé. | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 10:48 Mar 16 Nov 2010, 10:48 | |
| Solution probleme 26 : avec C.S on trouve : *&space;p(\frac{1}{x})&space;\geq&space;p(1)^{2}\geq&space;1) d'ou le resultat Probleme 27 :Dans un groupe de 17 personnes chaque couple de personnes s'échange du courrier sur un seul thème de réflexion (thème à choisir parmi 3 thèmes possibles). Montrer qu'il existe au moins 3 personnes qui s'échangent du courrier sur un même thème de réflexion.
Dernière édition par just-abdess le Mar 16 Nov 2010, 10:58, édité 1 fois | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 10:51 Mar 16 Nov 2010, 10:51 | |
| oui application direct.
a toi just-abdess. | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 10:52 Mar 16 Nov 2010, 10:52 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 11:55 Mar 16 Nov 2010, 11:55 | |
| @just-abdess : est-ce chaque personne parmi ces 17 s'échange avec tous les autres ? | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 11:59 Mar 16 Nov 2010, 11:59 | |
| oui , par exemple a1 s'echange avec a2 le theme B1 , avec a3 le theme B2 , avec a4 le theme B3 , .....etc | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 12:39 Mar 16 Nov 2010, 12:39 | |
| Solution du problème 27 :Notons les 17 personnes  et les trois thèmes  . D'après le principe de tiroirs 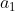 s'échange du courrier sur un même thème de réflexion 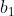 avec au moins 6 personnes. Si 2 de ces 6 personnes s'échangent du courrier sur le thème 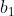 , alors nous tenons nos trois personnes. Supposons maintenant qu'aucun couple de ces 6 personnes ne s'échange du courrier sur le thème 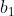 . D'après le principe de tiroirs, 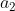 éhange du courrier avec au moins 3 de ces personnes sur un thème 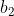 . Si 2 personnes parmi  et 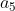 s'échangent du courrier sur le thème 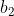 , alors, avec 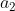 , nous avons trouvé nos trois personnes. Sinon, c'est que tous les couples parmi  s'échangent sur un thème autre que  donc sur 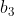 . Donc nous tenons nos trois personnes dans ce cas également. Sauf erreur. Au plaisir ! Edit : Problème 28 :Soient  . Montrez que : (b-1)(c-1)\geq%208)
Dernière édition par mizmaz le Mar 16 Nov 2010, 12:51, édité 2 fois | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 12:48 Mar 16 Nov 2010, 12:48 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 13:08 Mar 16 Nov 2010, 13:08 | |
| Solution au problème 28 :La condition est équivalente à :  Et l'inégalité est équivalente après développement à :  Qui est vraie d'après l'inégalité de Cauchy-Schwarz :  Problème 29 : Problème 29 : (* : une étoile) Trouver toutes les fonctions f :IR ->IR telles que : f(x²-y²)=(x-y)(f(x)+f(y)), pour tous réels x et y.
Dernière édition par Dijkschneier le Mar 16 Nov 2010, 14:40, édité 1 fois | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 14:04 Mar 16 Nov 2010, 14:04 | |
| Solution du probleme 29
pour x=-y , f(0) =2x(f(x)+f(-x)) ^1^
posons a=x+y et b=x-y
donc E.F est équivalent à f(ab)=b(f((a+b)/2)+f((a-b)/2))
donc avec b =1 et a =2X+1
E.F est equivalent à f(2X+1)=f(X+1)+f(X) , par X=-1 on va deduire que f(0) = 0
donc d'aprés ^1^ f(-x)=-f(x)
posons g(x)=f(x)/x pour tt x est different de 0
on a f(x²-y²)=(x-y)(f(x)+f(y)) d'autre part f(x²-(-y)²)=(x+y)(f(x)-f(y))
donc g(y)=g(x) , ce qui montre que la fonction g est constante donc
quelque soit x non nul g(x)=g(1)=f(1)
donc la fonction qui verifie l'equation f(x)=xf(1) quelque soit x dans IR(ce qui verifie vraiment EF)
sauf erreur
j'attend une confirmation ^_^
| |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 14:43 Mar 16 Nov 2010, 14:43 | |
| | |
|
  | |
just-abdess
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 30
Date d'inscription : 29/09/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 16:34 Mar 16 Nov 2010, 16:34 | |
| je n'ai pas un exo interessant pour le moment , je laisse l'honneur a quelqu'un d'autre de poster un exo ^_^ à vous .... | |
|
  | |
Mr.Wajih
Débutant

 Nombre de messages : 5 Nombre de messages : 5
Age : 30
Date d'inscription : 04/11/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 16:59 Mar 16 Nov 2010, 16:59 | |
| Et voilà ...  | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mar 16 Nov 2010, 22:48 Mar 16 Nov 2010, 22:48 | |
| bonsoir!!
si on prend m>n donc la valeur min de [m,n] est m. (dans ce cas on a m=nk k de IN)
dans l'enoncé on trouve 1/b + 1/c +1/d +1/e est max avec b est un multipbe de b,c est un multipe de b....... cela applique que b>=2,c>=4,d>=8 et d>=16
1/2 +1/4+ 1/8 +1/16 =15/16 d'ou le resultat.
PS :desole pour l'ecriture .
BONNE 3ID a tout les musulmans . | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 14:46 Mer 17 Nov 2010, 14:46 | |
| apres la bouffe de BOULFAFE,retournons au plaisir^^ exercoce proposé: Résourdre en IR² le systeme suivant:  . | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 15:20 Mer 17 Nov 2010, 15:20 | |
| Bon après-midi tout le monde  Solution du problème 31 - Spoiler:
En attente de confirmation . | |
|
  | |
marouan777
Maître

 Nombre de messages : 244 Nombre de messages : 244
Age : 31
Date d'inscription : 05/06/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 15:27 Mer 17 Nov 2010, 15:27 | |
| a toi tarask .on t'attend | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 15:46 Mer 17 Nov 2010, 15:46 | |
| Problème 32:Prouver que pour tous réels positifs a,b et c on a l'inégalité suivante :  EDIT: réels positifs ! Bonne chance  | |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 15:54 Mer 17 Nov 2010, 15:54 | |
| SOLUTION AU PROPblème 32 : - Spoiler:
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=52&t=377955
post 5
| |
|
  | |
Sporovitch
Maître

 Nombre de messages : 211 Nombre de messages : 211
Age : 30
Localisation : France
Date d'inscription : 06/09/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 16:06 Mer 17 Nov 2010, 16:06 | |
| Problème 33 - Sporovitch a écrit:
Probleme :

avec xy+xz+yz=1 Ce problème n'a pas encore de réponse . La réponse postée par m_zaynep était incomplète. | |
|
  | |
tarask
Expert sup

 Nombre de messages : 1004 Nombre de messages : 1004
Age : 31
Date d'inscription : 14/06/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Mer 17 Nov 2010, 16:15 Mer 17 Nov 2010, 16:15 | |
| - Sporovitch a écrit:
- SOLUTION AU PROPblème 32 :
- Spoiler:
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=52&t=377955
post 5
Euuh d'accord , en fait , c'est pas de là que je l'ai tirée  - Sporovitch a écrit:
- Problème 33
- Sporovitch a écrit:
Probleme :

avec xy+xz+yz=1 Ce problème n'a pas encore de réponse .
La réponse postée par m_zaynep était incomplète. Je ne l'avais pas remarqué ! Faute de temps, j'essayerai avec plutard | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 19 Nov 2010, 10:05 Ven 19 Nov 2010, 10:05 | |
| - Sporovitch a écrit:
Probleme :

avec xy+xz+yz=1 solution du problème33:- Spoiler:
posons xy=a , yz=b , zx=c l'inégalité à prouver devient:  avec a+b+c=1 ....Or d'après l'inégalité de Schur et puisque abc=<1/27 on a :  CQFD....
que chacun se sente libre de proposer un nouveau problème! | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Ven 19 Nov 2010, 10:46 Ven 19 Nov 2010, 10:46 | |
| Problème 34 : (** : deux étoiles)
Sur les cotés AB,BC,CD et AD d'un quadrilatère ABCD, et extérieurement à ce quadrilatère, on construit des carrés de centres respectifs O1,O2,O3 et O4.
Montrer que : (O1O3) _|_ (O2O4) et O1O3=O2O4. | |
|
  | |
majdouline
Expert sup

 Nombre de messages : 1151 Nombre de messages : 1151
Age : 31
Localisation : Ø
Date d'inscription : 04/01/2009
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 21 Nov 2010, 00:15 Dim 21 Nov 2010, 00:15 | |
| Solution du problème 34:- Spoiler:
on considère M le milieu de [AC] on considère r la rotation de centre B et d'angle 90° on a : =H%20\textsl{%20et%20}r(E)=A%20\right%20)\Rightarrow%20r(CE)=HA%20\Rightarrow%20CE=HA%20,%20(CE)\perp%20(HA)) on considère le triangle EAC on a : %20\parallel%20(EC)%20%20\textsl{%20et%20}%20MO_{1}=\frac{EC}{2}) on considère le triangle AHC on a : %20\parallel%20(AH)%20\textsl{%20et%20}%20MO_{2}=\frac{AH}{2}) alors : =(MO_{2})\textsl{%20et%20}(MO_{1})\perp%20(MO_{2})) --------------------------------------------------------------------- de la même manière on démontre que : =(MO_{4})\textsl{%20et%20}(MO_{3})\perp%20(MO_{4})) ------------------------------------------------------------------------------------ soit R la rotation de centre M et d'angle 90° on a : =O_{1}\textsl{%20et%20}R(O_{4})=O_{3})\Rightarrow%20{\color{red}%20R(O_{2}O_{4})=O_{1}O_{3}}) CQFD.... sauf erreur....
que chacun se sente libre de proposer un nouveau problème ! | |
|
  | |
stylo vs calculator
Maître

 Nombre de messages : 73 Nombre de messages : 73
Age : 30
Date d'inscription : 19/11/2010
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  Dim 21 Nov 2010, 11:58 Dim 21 Nov 2010, 11:58 | |
| Salut,
Probleme 35: prouvez que Pi < 22/7 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Retour au plaisir :) Sujet: Re: Retour au plaisir :)  | |
| |
|
  | |
| | Retour au plaisir :) |  |
|
