exo inégalité

P#19 : (Darij Grinberg)
a,b et c des réels strictement positifs :
M.Q :

OK voici ma solution pour P#19

P#20 :
Prouver que :

pour tous réels x,y et z dans [1,2].

Bonne chance

abdelkrim-amine a écrit:

P#20 :
Prouver que :

pour tous réels x,y et z dans [1,2].

Bonne chance

Je pense qu'il dépasse notre niveau Problem 4 vietnamese tst 2006
Libre a chacun de proposer une inégalité
P#20:
Prouver que:
[img]http://latex.codecogs.com/gif.latex?\prod&space;(a-\frac{1}{b})\geq&space;\prod&space;(a-\frac{1}{a})\forall&space;a,b,c\in&space;[1,+00) [/img]

diablo902 a écrit:

P#20:
Prouver que:

S#20 :


je vais posté une autre inégalité demain incha allah

P#21 :

a,b et c des réels strictement positifs tels que : 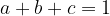et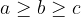

Montrer que :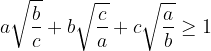

S#21:
https://mathsmaroc.jeun.fr/t18688-cool-inegalite#159324
Après ces étapes ,vu l’homogénéité on suppose que a²+b²+c²=1 et a'=a²,b'=b²,c'=c²
D'où notre inégalité
P#22:**Ukraine,2001
a,b,c,x,y,z des positives réels tel que : x+y+z=1.Prouver que

diablo902 a écrit:

S#21: P#22:**Ukraine,2001
a,b,c,x,y,z des positives réels tel que : x+y+z=1.Prouver que

S#22 :


P#23 :
a un réel positif tel que :
Montrer que :

S#23:
La 1ere inégalité est équivalente à
D'où

P#24:
a,b,c trois réels tels que a+b+c+1
Montrez que : v(4a+1)+v(4b+1)+v(4c+1)=< v(21)

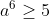Nas8 a écrit:

P#24:
a,b,c trois réels tels que a+b+c+1
Montrez que : v(4a+1)+v(4b+1)+v(4c+1)=< v(21)

Je pense que a+b+c=1
Posons 4a+1=A;4b+1=B;4c+1=C
Donc A+B+C=7
D'où notre inégalité est équivalente à
Ce qui est une application directe de Caushy Schwarz
P#25:
I le centre du cercle circonscrit du triangle ABC,D et E les milieux de [AB] et [AC].K:intersection de (DE) et (BI);L:Intersection de (DE) et (CI). Prouver que : AI+BI+CI>BC+KL

Nas8 a écrit:

P#24:
a,b,c trois réels tels que a+b+c+1
Montrez que :

S#24 :

diablo902 a écrit:

Nas8 a écrit:

P#24:
a,b,c trois réels tels que a+b+c+1
Montrez que : v(4a+1)+v(4b+1)+v(4c+1)=< v(21)

Je pense que a+b+c=1
Posons 4a+1=A;4b+1=B;4c+1=C
Donc A+B+C=7
D'où notre inégalité est équivalente à
Ce qui est une application directe de Caushy Schwarz

dsl diablo902 Je n'ai pas vu votre msg
C'est ton tour pour posté un exo

diablo902 a écrit:

Exercice 15 :
a,b,c des positives réels prouver que :

<a href="http://www.codecogs.com/eqnedit.php?latex=\bg_black \frac{c}{a@plus;2b}= \frac{ac}{a^{2}@plus;2ab@plus;b^{2}-b^{2}}=\frac{c}{a@plus;b} on suppose b\geqslant c\geqslant a qui nous donne l églité vrai \frac{c}{a@plus;b}@plus;\frac{b}{a@plus;c}=\frac{ac@plus;c^{2}@plus;ab@plus;b^{2}}{a^{2}@plus;ab@plus;ac@plus;bc}\geqslant 1" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\bg_black \frac{c}{a+2b}= \frac{ac}{a^{2}+2ab+b^{2}-b^{2}}=\frac{c}{a+b} on suppose b\geqslant c\geqslant a qui nous donne l églité vrai \frac{c}{a+b}+\frac{b}{a+c}=\frac{ac+c^{2}+ab+b^{2}}{a^{2}+ab+ac+bc}\geqslant 1" title="\bg_black \frac{c}{a+2b}= \frac{ac}{a^{2}+2ab+b^{2}-b^{2}}=\frac{c}{a+b} on suppose b\geqslant c\geqslant a qui nous donne l églité vrai \frac{c}{a+b}+\frac{b}{a+c}=\frac{ac+c^{2}+ab+b^{2}}{a^{2}+ab+ac+bc}\geqslant 1" /></a>