exo inégalité

DESOLE les 3 dernieres lignes ne sont pas en ordre c'est l'inversion
il me manque les guillemets pour la ligne 3

hind nassri a écrit:

abdelkrim-amine a écrit:

exercice 12:
a,b et c des réels positives. tels que: a+b+c=1
Montrer que :

Bonne chance

Selon C.S.
C.Q.F.D

(a;b;c;d)>0 et abcd=1

Demontrez que : a²+b²+c²+d²+ab+ac+ad+bd+bc+cd >= 10

hind nassri a écrit:

(a;b;c;d)>0 et abcd=1

Demontrez que : a²+b²+c²+d²+ab+ac+ad+bd+bc+cd >= 10

AM;GM

comment s'il vous plait diablo902 AM;GM

diablo902 a écrit:

abdelkrim-amine a écrit:

diablo902 a écrit:

Exercice 13 : (Zhautykov Olympiad 2008)
a,b,c des réels positives tels que abc=1

Solution exercice 13 :

Spoiler:

merci diablo902 pour cette inégalité

Peux tu m'expliquer le passage de l'inégalité de Chebyshev .Je pense qu'il est faux car on a selon HM-AM:

dsl je n'ai pas fait attention
en tous cas l'inégalité est un peu compliqué
pour la solution entrer ici Pro 25 page 8 et la solution dans les pages 26-27

j'ai representé la solution de l'exercice abdelkrim

hind nassri a écrit:

comment s'il vous plait diablo902 AM;GM

l'inégalité de AM-GM voir la page 43 dans ce livre

je n'arrive pas a acceder a ce lien je ne sais po pq

hind nassri a écrit:

je n'arrive pas a acceder a ce lien je ne sais po pq

Le premier et le 2eme c'est le même lien

je ne peux pas acceder aux deux


merci bcp abdelkrim pour votre aide c tres gentil

hind nassri a écrit:

je ne peux pas acceder aux deux


merci bcp abdelkrim pour votre aide c tres gentil

voici la page des inegalités si le lien ne marche pas

et pour la solution du prob du diablo902

merci bcp vous etes vrm tres gentil
ce lien est tres important; malheureusement ça ne marche pas avec moi

ça y'est tt est bien j'ai telechargé le livre

merci pour vous est ce que vous avez d'autre lien d'exercices et solutions

abdelkrim-amine a écrit:

Exercice 14 :

a=b=c=3/4

diablo902 a écrit:

abdelkrim-amine a écrit:

Exercice 14 :

a=b=c=3/4

c'est dans le livre écrit comme ça
moi aussi j'ai montrer que :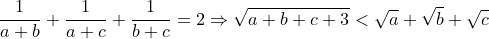

et je l'ai posé pour assurer

Exercice 15 :
a,b,c des positives réels prouver que :

diablo902 a écrit:

Exercice 15 :
a,b,c des positives réels prouver que :

Selon Cauchy Shwarz:



Et on sait que: selon AM-Gm
D'où le résultat!

salut a tous
voici une petite inégalité
Exercice 16 : (Olympiades du pacifique asiatique-96)
soient a,b et c les longueurs des côtés d'un triangle. Démontrer que :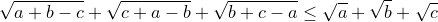

et déterminer le cas d'égalité
Bonne chance

abdelkrim-amine a écrit:

salut a tous
voici une petite inégalité
Exercice 16 : (Olympiades du pacifique asiatique-96)
soient a,b et c les longueurs des côtés d'un triangle. Démontrer que :

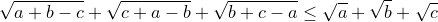
et déterminer le cas d'égalité
Bonne chance

S#16 :
On a a,b et c les longueurs des côtés d'un triangle donc a+b-c>=0 d'où d'où
Le même pour les 2 autres ; en sommant le résultat découle ...
Cas d'égalité a=b=c ou le triangle est équilatéral
P#17 :(**)
a,b,c des réels positives. Prouver que

slt tt le monde
voici un EXERCICE
(x;y)€R et on a x^3 + y^3 =2
est ce que cette inégalité x + y >=2 est juste ??

bonne chance

hind nassri a écrit:

slt tt le monde
voici un EXERCICE
(x;y)€R et on a x^3 + y^3 =2
est ce que cette inégalité x + y >=2 est juste ??

bonne chance

voici la réponse Hind

on propose que x+y >= 2 juste

on aura: x^3 + 3x²y + 3xy² + y^3 >= 8
d'ou: 2 +3xy(x+y) >= 8

xy(x+y) >= 2

xy >= 1 ou 0 >= xy (car x+y >= 2/xy )

puisque (x;y)€R donc xy € ]-infini; 0] U [1; +infini[ n'est pas forcément vrai

alors x + y >=2 n'est pas juste

sauf erreur