| | préparation aux olympiades |  |
|
+9legend-crush nmo abdelbaki.attioui boubou math killua 001 Syba alidos Oty Eurêka!! 13 participants |
|
| Auteur | Message |
|---|
Eurêka!!
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 20/04/2012
 |  Sujet: préparation aux olympiades Sujet: préparation aux olympiades  Mar 13 Nov 2012, 21:28 Mar 13 Nov 2012, 21:28 | |
| je crée cette page afin de préparer les olympiades nationales .
tout qui veut participer , il participe mais en suivant les régles.
la principale régle de cette préparation :
-exercice + corrigés+ exercices + ...........
-inégalité+eq.fonctionels+arithmetique+algebre(poly+....)+géometrie {Attention dans cet ordre}
-Il faut que la solution soit lisisble même si elle n'est pas rédigée en Latex.
-Si on ne parvient plus à résoudre un problème, dans un délai de 24 heurs, il sera modifié.
-ne pas poster d'hors sujet.
on commence maintenant.
bonne chance.
Dernière édition par Eurêka!! le Mer 14 Nov 2012, 21:49, édité 1 fois | |
|
  | |
Eurêka!!
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 20/04/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mar 13 Nov 2012, 21:28 Mar 13 Nov 2012, 21:28 | |
| determiner toutes les fonctions f:R*+ --->R*+ verifiant:
(x+y)(f(yf(x)))=x²(f(x)+f(y)) (pr tt x;y >0 ) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mar 13 Nov 2012, 21:55 Mar 13 Nov 2012, 21:55 | |
| salut , voici ma solution .
On a :
P(x,y) => (x+y)f(yf(x))=x²(f(x)+f(y))
P(y,x)=> (x+y) f(xf(y))=y² (f(x)+f(y))
d'ou , on obtient :
f(yf(x))\x² =f(xf(y))\y² quelque soit x , y > 0 (I) .
Maintenant :
P(x,1) => (x+1)f(f(x))=x²f(x)+xf(1) , donc f(f(x))=(x²f(x)+xf(1))(x+1)
soit a et b tel que f(a)=f(b) , on a d'apres l"égalité précédente :
(a²f(a)+af(1))(b+1)=(b²f(b)+bf(1))(a+1) on pose f(a)=f(b)=c et f(1)=d
equivelent a :
(a-b)(d+c(ab+a+b))=0 d'ou a=b , car l'autre terme est > 0 et donc
f est injective :
et finalement en prenant y=1 dans I on obtient :
f(f(x))=x²f(xf(1)) .
P(1,1) => f(f(1))=f(1)=> f(1)=1 et donc
f(f(x))=x²f(x) . en prenant y=1 dans l'equation initial on a :
(x+1)f(f(x))=x²(f(x)+1) donc (x+1)x²f(x)=x²f(x)+x² et donc
f(x)=1\x quelque soit x > 0 .
réciproque la fonction vérifie l'equation d'ou la conclusion | |
|
  | |
Eurêka!!
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 20/04/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mar 13 Nov 2012, 23:23 Mar 13 Nov 2012, 23:23 | |
| tres bonne démonstration sauf un petit souci par ici: - Oty a écrit:
- salut , voici ma solution .
Maintenant :
P(x,1) => (x+1)f(f(x))=x²f(x)+xf(1) , donc f(f(x))=(x²f(x)+xf(1))(x+1)
soit a et b tel que f(a)=f(b) , on a d'apres l"égalité précédente :
(a²f(a)+af(1))(b+1)=(b²f(b)+bf(1))(a+1) on pose f(a)=f(b)=c et f(1)=d
equivelent a :
(a-b)(d+c(ab+a+b))=0 d'ou a=b , car l'autre terme est > 0 et donc
f est injective :
j'ai l'impression que t'as oublier un ² P(x,1) => (x+1)f(f(x))=x²f(x)+x ²f(1) et avec les memes changements que t'as fais on aura (b-a)(c+d)(a+b+ab)=0 d'ou l'injectivité a toi de proposer un exercice | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 14 Nov 2012, 00:16 Mer 14 Nov 2012, 00:16 | |
| vu que Oty a tardé je propose cet exercice !! déterminez tous les (x,y) £ Z tel que 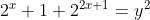 | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 14 Nov 2012, 14:25 Mer 14 Nov 2012, 14:25 | |
| Si y est pair, alors: x=0 ou x=1/2 (x £ Z) ==> x=0 ==> y = 2 ou y = -2 .
S={(0,-2);(0,2)}
Dernière édition par Syba le Mer 14 Nov 2012, 18:07, édité 3 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 14 Nov 2012, 14:44 Mer 14 Nov 2012, 14:44 | |
| - Syba a écrit:
- Si y est pair, alors: x=0 ou x=1/2 (x £ Z) ==> x=0 ==> y = 2 ou y = -2 .
Si y est impair, alors: il existe un entier k, tel que: y = 2k+1.
D'ou: 2^x(1+2^(x+1))=4k(k+1)
Alors: 2^x = 4k et 1+2^(x+1) = k+1
Donc: 8k+1=k+1
Alors: k = 0, ce qui est absurde (en remplacant dans des relations précédentes).
Conclusion:
S={(0,-2);(0,2)} il te manque des solution (4.23) par exemple | |
|
  | |
Eurêka!!
Féru
 Nombre de messages : 30 Nombre de messages : 30
Age : 29
Date d'inscription : 20/04/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 14 Nov 2012, 19:51 Mer 14 Nov 2012, 19:51 | |
| "y" est pair si et seulement si x=0 donc y=2 ou y=-2
pour le cas de y impair la démonstration est compliqué mais on peut déduir que (4,23) et (4,-23) sont aussi des solutions
une demonstration de la part d' alidos m'interesse bcp | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 14 Nov 2012, 21:12 Mer 14 Nov 2012, 21:12 | |
| y'en a que 2 personne qui ont essayé de résoudre cet exo je suppose , d'ici 24 heures si personne ne propose pas une solution , je le ferai moi meme  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Jeu 15 Nov 2012, 21:42 Jeu 15 Nov 2012, 21:42 | |
| alidos , c'est a toi de poster la solution  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 16 Nov 2012, 19:16 Ven 16 Nov 2012, 19:16 | |
| L'exercice 2 est très connu (P4 IMO 2006) inutile de poster ce genre d'exo dans un marathon .Je propose EXO 3 pour continuer . Résoudre dans Z l'équation suivante :  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 17 Nov 2012, 16:59 Sam 17 Nov 2012, 16:59 | |
| ce probleme ausssi et trés connu  .... c'est le premier exo 2em stage 2011 a rabat  .... . cette equation n'admet pas de solution dans Z | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 17 Nov 2012, 17:21 Sam 17 Nov 2012, 17:21 | |
| exo: 4
Montrer que l'equation : (x+1)²+(x+2)²+...+(x+2001)²=y² n'admet pas de solutions dans Z | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 18 Nov 2012, 10:56 Dim 18 Nov 2012, 10:56 | |
| Solution du problème 4supposons que l'équation admet une solution (x,y) dans Z l'équation est équivalente à x+(1^2+2^2+....+&space;2001^2)=y^2\Leftrightarrow&space;2001x^2+2001.2002x+(1^2+2^2+....+&space;2001^2)=y^2) parmi les nombre ) il existe exactement 2001/3 multiple de trois , et 2001*2/3 nombre congrue à 1 modulo 3(un carré est congrue à 1 ou à 0 modulo 3) ainsi est puisque les deux premier thermes sont des multiple de trois il nous vient que est donc [img]http://latex.codecogs.com/gif.latex?LHS\equiv&space;1334\left&space;[&space;3&space;\right&space;]\equiv&space;2\left[3\right][/img] [img] http://latex.codecogs.com/gif.latex?y^2\equiv&space;2\left[3\right] [/img] absurd. CQFD
Dernière édition par boubou math le Dim 18 Nov 2012, 12:36, édité 1 fois | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 18 Nov 2012, 11:32 Dim 18 Nov 2012, 11:32 | |
| 1^2+...+2001^2=2001 2002 4003 /6
= 667 1001 4003
=(3*222+1)(3*333+2)(3*1334+1)
= 2 [3] | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 18 Nov 2012, 12:54 Dim 18 Nov 2012, 12:54 | |
| a vous de proposer  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 19 Nov 2012, 14:33 Lun 19 Nov 2012, 14:33 | |
| boubou : a toi de proposer un blem  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 19 Nov 2012, 18:31 Lun 19 Nov 2012, 18:31 | |
| J'étais sur le point de le faire quand j'ai vue qu'oty avait déjà poster un exo. Problème 5 a,b et c sont trois réel positifs tels que a+b+c=1 ,montrer que :  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 19 Nov 2012, 19:48 Lun 19 Nov 2012, 19:48 | |
| ma solution au problem 5 :
on pose : m=\sum ab et n=abc l'inégalité est equivalente a :
1-3m+9n >= 1\4
premier cas : si m=< 1\4
alors on a bien LHS >= 1-3\4 +9r=1\4 + 9r >= 1\4 .
cas de m >=1\4 , par shur on a :
n >= (4m-1)\9
donc il suffit de prouver que :
1-3m+(4m-1) >= 1\4 equivalent a
m >= 1\4 ce qui est vrai . | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mar 20 Nov 2012, 13:05 Mar 20 Nov 2012, 13:05 | |
| Bien ,à toi  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mar 20 Nov 2012, 19:38 Mar 20 Nov 2012, 19:38 | |
| Probleme 6
soit f une fonction numérique définie sur R+ tele que :
x->f(x)-x^3 et x->f(x)-3x sont deux fonction croissantes sur R+ .
Montrer que :
x->f(x)-x-x² est aussi une fonction croissante sur R+ . | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 02 Déc 2012, 13:59 Dim 02 Déc 2012, 13:59 | |
|
Dernière édition par alidos le Lun 03 Déc 2012, 19:13, édité 1 fois | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 02 Déc 2012, 14:02 Dim 02 Déc 2012, 14:02 | |
| Le Problème 6 est encore en Jeu .
Dernière édition par alidos le Lun 03 Déc 2012, 19:13, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 03 Déc 2012, 18:47 Lun 03 Déc 2012, 18:47 | |
| - alidos a écrit:
- solution du Problème 6
u:x->f(x)-x^3 croissante sur lR+ donc le dérivé atkone positif
alors f'(x)>=2x²
et v:x->f(x)-3x l'ai aussi , alors f'(x)>=3
w le dérivé dial la fonction x->f(x)-x-x² est
f'(x)-1-2x
si x£[0.1] ALORS -1-2x>=-3 et on a f'(x)>=3 donc f'(x)-1-2x positif si x£[0.1]
SI x£[1;+oo[ on a f'(x)>=3x² donc
f'(x)-1-2x²>=3x² -1-2x²=x²-1>=0
donc le dérivé dial x->f(x)-x-x² est positif sur lR+ alors la fonction est croissante On a aucune information sur la dérivabilité de de f . je pense que le faite d'utilisé quelque résultats sur la monotonie d'une composé peut aider . | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 03 Déc 2012, 19:12 Lun 03 Déc 2012, 19:12 | |
| Ah Oui tu as raison,j'ai pas fait attention à ce détail , je retire ma réponse , le Problème 6 est encore en jeu .  | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  | |
| |
|
  | |
| | préparation aux olympiades |  |
|
