| | préparation aux olympiades |  |
|
+9legend-crush nmo abdelbaki.attioui boubou math killua 001 Syba alidos Oty Eurêka!! 13 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 22 Déc 2012, 01:00 Sam 22 Déc 2012, 01:00 | |
| - Oty a écrit:
- Probleme 6
soit f une fonction numérique définie sur R+ tele que :
x->f(x)-x^3 et x->f(x)-3x sont deux fonction croissantes sur R+ .
Montrer que :
x->f(x)-x-x² est aussi une fonction croissante sur R+ . Soit 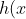=f(x)-x^3) , =f(x)-3x) et =f(x)-x-x^2) . Soient x et y deux réels strictement positifs, Puisque h est croissante, alors -h(y)}{x-y}\ge0) , ou encore -f(y)}{x-y}\ge x^2+xy+y^2) .==>(1) Puisque k est croissante, alors -k(y)}{x-y}\ge0) , ou encore -f(y)}{x-y}\ge 3) .==(2) On a d'autre part, -g(y)}{x-y}=\frac{f(x)-f(y)}{x-y}-(1+x+y)) . ***Le premier cas: si x et y sont inférieurs à 1. On a  et selon 2, il vient -f(y)}{x-y}) donc -g(y)}{x-y}\ge0) . Donc g est croissante sur ]0,1]. ***Le deuxième cas: si x et y sont supérieurs à 1. On a  ,  et  . Donc  et selon 1, il vient -f(y)}{x-y}) donc -g(y)}{x-y}\ge0) . Donc g est croissante sur [1,  [. ***Conclusion: g est croissante sur ]0,1] et sur [1,  [. Donc g est croissante sur [0,  [. CQFD. Sauf erreurs! | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 23 Déc 2012, 13:10 Dim 23 Déc 2012, 13:10 | |
| Poste un exo stp  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 23 Déc 2012, 18:37 Dim 23 Déc 2012, 18:37 | |
| - boubou math a écrit:
- Poste un exo stp
 Si vous avez étudiez les matrices, voici un problème: Soit la matrice définie par: &\sin(\theta) \\\sin(\theta) &\ a+\cos(\theta)\end{pmatrix}) . Calculez 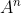 , pour tout entier naturel n. (  et :A^n=A^{N-1}.A) .) Sinon, calculez la somme: } } \right)} ) où n et p sont des entiers naturels donnés. Bonne chance. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Jeu 17 Jan 2013, 17:57 Jeu 17 Jan 2013, 17:57 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Mer 23 Jan 2013, 22:55 Mer 23 Jan 2013, 22:55 | |
| - legend-crush a écrit:
- pas encore étuidés ^^
Donc, il faut calculer la somme que j'ai proposée... | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Jeu 24 Jan 2013, 23:14 Jeu 24 Jan 2013, 23:14 | |
| Solution Pour le 2:
Notation je note pout tout entier naturel l et tout entier naturel k: [p"k] egale a k (parmi p).
On note aussi A la somme recherchée.
Donc A=sum(0->n)(((i+p)!)/i!)
Ainsi A=(p!)sum(0->n)([i+p"p])
Donc A=(p!)sum((-p)->n)([i+p"p])
Donc par changement d'indices:
A=(p!)sum(0->n+p)([j"p])
Donc A=(p!)[(n+p+1)"(p+1)]
Cette derniere egalité est bien connue mais c'est aussi demontrable par simple recurrence. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Jeu 24 Jan 2013, 23:46 Jeu 24 Jan 2013, 23:46 | |
| - nmo a écrit:
Si vous avez étudiez les matrices, voici un problème:
Soit la matrice définie par: &\sin(\theta) \\\sin(\theta) &\ a+\cos(\theta)\end{pmatrix}) . .
Calculez 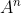 , pour tout entier naturel n. , pour tout entier naturel n.
( et et :A^n=A^{N-1}.A) .) .)
Sinon, calculez la somme: } } \right)} ) où n et p sont des entiers naturels donnés. où n et p sont des entiers naturels donnés.
Bonne chance. Au debut quand j'ai vu ce problème il y a quelque jour il ne m'inspirait rien de bon , je viens d'y retourner aujourd hui il y a quelque heure et Hamdoullah tout semblé plus facile avec l'aide du stage que je poursuis en ce moment a Edukaty , Ma solution pour le Probleme 2 est similaire que celle de Yasserito , sauf qu'il fut plus rapide a posté  . Voici en détaille ma solution : on Note S la somme voulu : ...(i+p))=(1.2....p)+2....(p+1)+&space;3...(p+3)+...+(n+1)..(n+p)=\sum_{k=0}^{n}\frac{(p+k)!}{k!}=p!\sum_{k=0}^{n}\binom{p+k}{k}=p!\binom{p+n+1}{n}) malheureusement pour le résultat final je n'ai pas trouver un autre moyen que le conjecturé puis le prouver par récurrence , nmo avez vous une manière plus direct pour le prouver sans récurrence ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 00:46 Ven 25 Jan 2013, 00:46 | |
| - Oty a écrit:
- malheureusement pour le résultat final je n'ai pas trouver un autre moyen que le conjecturé puis le prouver par récurrence , nmo avez vous une manière plus direct pour le prouver sans récurrence ?
Non, je ne connais aucune autre méthode; il n'y a que la récurrence. Je vous propose un nouvel exercice, que j'ai apprécié: Soit f une fonction définie de l'ensemble des réels vers lui même, vérifiant: :f\circ f(x)=-x) . Montrez que f n'est pas continue sur I. Bonne chance.
Dernière édition par nmo le Ven 25 Jan 2013, 16:02, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 11:53 Ven 25 Jan 2013, 11:53 | |
| Par absurde, on suppose que f est continue , comme elle est injective donc elle est strictement monotone donc fof est strictement croissante ce qui est bien évidemment faux. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 13:47 Ven 25 Jan 2013, 13:47 | |
| - yasserito a écrit:
- Par absurde, on suppose que f est continue , comme elle est injective donc elle est strictement monotone donc fof est strictement croissante ce qui est bien évidemment faux.
C'est une très bonne solution! A toi de proposer un nouvel exercice... | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 15:33 Ven 25 Jan 2013, 15:33 | |
| Je vous propose deux exercices:
Trouvez toutes les fonctions C1 f definies sur IR et a valeurs reelles telles que:
fof=f.
Existe il une surjection continue de [0,1[ vers IR.
P.S/ c'etait quoi ta solution nmo pour l'exo precedent? | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 15:50 Ven 25 Jan 2013, 15:50 | |
| - yasserito a écrit:
- Par absurde, on suppose que f est continue , comme elle est injective donc elle est strictement monotone donc fof est strictement croissante ce qui est bien évidemment faux.
excusez moi mais il me semble qu'il y a une erreur , quand tu suppose par l'absure que f est continue , il faut faire attention au quantificateur , l'absurde c'est il existe xo sur le quelle f est continue , non ? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 16:05 Ven 25 Jan 2013, 16:05 | |
| - Oty a écrit:
- yasserito a écrit:
- Par absurde, on suppose que f est continue , comme elle est injective donc elle est strictement monotone donc fof est strictement croissante ce qui est bien évidemment faux.
excusez moi mais il me semble qu'il y a une erreur , quand tu suppose par l'absure que f est continue ,
il faut faire attention au quantificateur , l'absurde c'est il existe xo sur le quelle f est continue , non ?
Je vois que c'est le contraire, c'est en ce qu'on doit démontrer qu'on a le quantificateur existentiel. La supposition de yasserito nous ramène au quantificateur universel. - yasserito a écrit:
- P.S/ c'etait quoi ta solution nmo pour l'exo precedent?
C'est la même solution que j'avais en tête. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 16:16 Ven 25 Jan 2013, 16:16 | |
| - Oty a écrit:
- yasserito a écrit:
- Par absurde, on suppose que f est continue , comme elle est injective donc elle est strictement monotone donc fof est strictement croissante ce qui est bien évidemment faux.
excusez moi mais il me semble qu'il y a une erreur , quand tu suppose par l'absure que f est continue ,
il faut faire attention au quantificateur , l'absurde c'est il existe xo sur le quelle f est continue , non ?
Bonjour, c'est le contraire car( f n'est pas continue <=> il existe x tel que f n'est pas continue en x) La question dont la réponse sera la votre est: Montrer que f n'est pas continue en aucun point de Df. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Ven 25 Jan 2013, 22:31 Ven 25 Jan 2013, 22:31 | |
| Ah oui vous avez raison j'ai mal lu la question , Merci beaucoup . bah comme l'analyse est assez apprécier je propose le problème suivant si yasserito ne voit pas d’inconvénient . Problème soit (an)n>=0 une suite a valeurs positives qui vérifient : pour tout entiers naturels m et n .  ou C est une constante positive . Prouver que ) est convergente . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 26 Jan 2013, 00:28 Sam 26 Jan 2013, 00:28 | |
| - yasserito a écrit:
- Je vous propose deux exercices:
Trouvez toutes les fonctions C1 f definies sur IR et a valeurs reelles telles que: fof=f. Voici une solution célèbre de ce problème:  . Au plaisir! | |
|
  | |
Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 26 Jan 2013, 11:46 Sam 26 Jan 2013, 11:46 | |
| - Oty a écrit:
- nmo a écrit:
Si vous avez étudiez les matrices, voici un problème:
Soit la matrice définie par: &\sin(\theta) \\\sin(\theta) &\ a+\cos(\theta)\end{pmatrix}) . .
Calculez 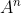 , pour tout entier naturel n. , pour tout entier naturel n.
( et et :A^n=A^{N-1}.A) .) .)
Sinon, calculez la somme: } } \right)} ) où n et p sont des entiers naturels donnés. où n et p sont des entiers naturels donnés.
Bonne chance. Au debut quand j'ai vu ce problème il y a quelque jour il ne m'inspirait rien de bon , je viens d'y retourner aujourd hui il y a quelque heure et Hamdoullah tout semblé plus facile avec l'aide du stage que je poursuis en ce moment a Edukaty , Ma solution pour le Probleme 2 est similaire que celle de Yasserito , sauf qu'il fut plus rapide a posté  . Voici en détaille ma solution : . Voici en détaille ma solution :
on Note S la somme voulu :
...(i+p))=(1.2....p)+2....(p+1)+&space;3...(p+3)+...+(n+1)..(n+p)=\sum_{k=0}^{n}\frac{(p+k)!}{k!}=p!\sum_{k=0}^{n}\binom{p+k}{k}=p!\binom{p+n+1}{n})
malheureusement pour le résultat final je n'ai pas trouver un autre moyen que le conjecturé puis le prouver par récurrence , nmo avez vous une manière plus direct pour le prouver sans récurrence ? Salut Oty, j'avais une question le calcul de la somme double et tout à fait le même que j'ai suivis, sauf pour la somme des combinaisons, comment tu as pu conjecturer, une telle somme en fonction des combinaisons? @nmo: d'autres sommes (également doubles) seront les bienvenus, pour se familiariser un peu avec  . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 | |
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 | |
  | |
Mohammed_Lahlou
Maître
 Nombre de messages : 79 Nombre de messages : 79
Age : 28
Localisation : Tanger
Date d'inscription : 21/07/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Sam 26 Jan 2013, 20:35 Sam 26 Jan 2013, 20:35 | |
| Je propose un exercice en complexe que je trouve interessant.
Demontrez que ABC est equilateral si et seulement si a^2+b^2+c^2 = ab+ac+bc
Avec A, B et C daffixe respectivement a ,b et c | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 27 Jan 2013, 00:33 Dim 27 Jan 2013, 00:33 | |
| Bonsoir, je propose cette solution:
ABC equilateral
<==>
AB=AC
AB,AC = Pi/3 [2Pi]
(ou -Pi/3 ca donne le meme resultat en elveant au carre)
<==>
(b-a)/(c-a)=1/2+(V3/2)i
<==>
[(b-a)/(c-a)-1/2]²=-3/4
<==>
(b²-2ab+a²)/(c²-2ac+c²)-(b-a)/(c-a)+1=0
<==>
(b²-2ab+a²)/(c-a) -b+c=0
<==>
b²-2ab+a²-bc+c²+ab-ac=0
<==>
a²+b²+c²=ab+bc+ac | |
|
  | |
Geo
Habitué
 Nombre de messages : 24 Nombre de messages : 24
Age : 32
Date d'inscription : 13/07/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Dim 27 Jan 2013, 23:43 Dim 27 Jan 2013, 23:43 | |
| ABC équilatéral <==> a=b=c <==> (a-b)²+(b-c)²+(c-a)²=0 <==> a²+b²+c²=ab+bc+ca  | |
|
  | |
Humber
Expert grade2
 Nombre de messages : 310 Nombre de messages : 310
Age : 27
Date d'inscription : 10/10/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 28 Jan 2013, 00:03 Lun 28 Jan 2013, 00:03 | |
| - Geo a écrit:
- ABC équilatéral <==> a=b=c <==> (a-b)²+(b-c)²+(c-a)²=0 <==> a²+b²+c²=ab+bc+ca
 Je ne comprend pas ce qui est en rouge ? ! Est-ce une propriété ? | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 28 Jan 2013, 12:38 Lun 28 Jan 2013, 12:38 | |
| Lol a=b=c <==> A=B=C <==> ABC est un point, et non un triangle  | |
|
  | |
Syba
Maître

 Nombre de messages : 132 Nombre de messages : 132
Age : 29
Date d'inscription : 08/09/2012
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  Lun 28 Jan 2013, 15:47 Lun 28 Jan 2013, 15:47 | |
| Je vous propose 2 jolis exos: 1) 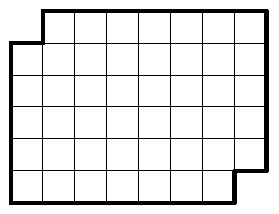 On considère ce plateau de jeu. On souhaite le paver(couvrir) de dominos à 2 cases(qu'on peut disposer soit horizontalement soit verticalement). Est-ce possible ? 2) Trouver tous les entiers strictement positifs x, y et z tel que: 1/x + 1/y + 1/z = 1
Dernière édition par Syba le Lun 28 Jan 2013, 16:05, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: préparation aux olympiades Sujet: Re: préparation aux olympiades  | |
| |
|
  | |
| | préparation aux olympiades |  |
|
