#Grand Jeu d'été (2007 ) TSM EST COMENCE ==>

jack a écrit:

quelle rége tu as étuliser premiérement quand tu as dit f(-x^3)=-f(x)^3

on a : f(f(x) = -x^3 => f(f(f(x) = f(-x^3)

et on a : f(f ( f(x) ) = -f(x)^3

d'ou f(-x^3) = -f(x)^3

slt
j'attends une confirmation de ma soution pour que je puisse poster un nouvel exo.

wiles a écrit:

exo1:
on peut aisement prouver que : f(-x^3)=-f(x)^3
donc f(0)=0
et on a f(1)=-f(-1)^3 et f(-1)=-f(1)^3
donc f(1)=f(1)^9
alors f(1)=0 ou f(1)=1 ou f(1)=-1
*si f(1)=0 alors f0f(1)=f(0)=0
mais d'apres la condition f0f(1)=-1 contradiction
*si f(1)=1 alors f0f(1)=f(1)=1
mais d'apres la condition f0f(1)=-1 contradiction
*si f(1)=-1 alors f(-1)=-1 donc f0f(-1)=f(-1)
mais d'apres la condition f0f(-1)=1 contradiction
il n'existe donc aucune application qui realise les conditions du probleme
demonstration achevee.
exo2:
a petites valeurs on peut tres bien prouver que f(n)=1-n
exemple:
f(0)=1 donc f0f(0)=f(1) donc f(1)=0
f(f(1)+2))=-1 donc f(-1)=2
prouvons par recurrence que f(n)=1-n
pour cela on supose que pour un certain n de N qulqsoit k tel que -n<=k<=n on a f(k)=1-k
on doit prouver que f(n+1)=-n et f(-n-1)=n+2
pour n=1 la propriete est vrai
*prouvons que f(n+1)=-n
on a f(f(n+2)+2)=n
en remplacant n ar -n on aura
f(f(2-n)+2)=-n
et puisque -n<=2-n<=n
alors f(2-n)=n-1
donc f(n+1)=-n
*prouvons que f(-n-1)=n+2
on a f(f(n+2)+2)=n donc f0f(f(n+2)+2)=f(n)
donc f(n+2)+2=f(n)
en remplacant n par -n-1 on trouve que:
f(-n-1)=f(1-n)+2
et puisque -n<=1-n<=n
on a f(1-n)=n
donc f(-1-n)=n+2
recurrence achevee.

salut
pour le premier exo c juste .
mais pour le deuxieme je vois que tu as utilusé la reccurence pour les entier negatifs.!
je crois.

desole selfrespect mais la reccurence je l'ai faite sur n qui est un nombre entier

"un certain n de N qulqsoit k tel que -n<=k<=n on a f(k)=1-k
on doit prouver que f(n+1)=-n et f(-n-1)=n+2"
biensure cest une reccurence sur un entier .

we donc ma recurence est clean

wiles a écrit:

we donc ma recurence est clean

la reccurence ne se fait que sur les entiers naturel mais je vois (que tu las utilusé pour des entier <0
tu as dit :
"un certain n de N qulqsoit k tel que -n<=k<=n on a f(k)=1-k
on doit prouver que f(n+1)=-n et f(-n-1)=n+2"
(cela ne veut pas dire que tt la reponse est fausse p etre la redactyion qui est fausse )
(pkoi tu nas pas fait les etapes classique reccur sur N PUIS PASSAGE AU RELATIFS p etre tu voulu racourcir la demo !?)

pour mon idee je crois qu'elle est juste
considerons la propriete "klquesoit k de (-n;n) on a f(k)=1-k"
pour n=1 la propriete est vrai
suposons que la propriete est vrai pour un certain n de N ET PROUVONS QU'ELLE EST VRAI POUR N+1
pour prouver que la propriete est vrai pour n+1 cad "klquesoit k de (-(n+1);(n+1)) on a f(k)=1-k" il suffit de prouver que f(-n-1)=2+n et f(n+1)=-n
et c ce que j'ai fait dans ma demonsration
j'espere que j'ai ete clair

wiles a écrit:

pour mon idee je crois qu'elle est juste
considerons la propriete "klquesoit k de (-n;n) on a f(k)=1-k"
pour n=1 la propriete est vrai
suposons que la propriete est vrai pour un certain n de N ET PROUVONS QU'ELLE EST VRAI POUR N+1
pour prouver que la propriete est vrai pour n+1 cad "klquesoit k de (-(n+1);(n+1)) on a f(k)=1-k" il suffit de prouver que f(-n-1)=2+n et f(n+1)=-n
et c ce que j'ai fait dans ma demonsration
j'espere que j'ai ete clair

ben tu as posé" P(n):klquesoit k de (-n;n) on a f(k)=1-k " ce nest pas un problem
est ce que tu peu la demontrer sans utiluser la reccurence car ce nest pas qsa place ,
ben le principê de la reccurence est le suivant
P(n)==> P(n+1)
alors pour ~ -n ~ celon ce que tu dis !
P(-n) ==> P(-n+1) !! est ce que tu crois que cest vrai !

merci conan j'ai compris

salut tout le monde.
bon la réponse de la première question est correcte,pour la deuxième elle est correcte au niveau de la résultat mais n'est pas bien prouvée car Wiles n'a pas bien réspecté les étapes de la récurrence.demain je vais posté ma solution pour la question 2 et 3.mais maintenant Wiles doit poster son exo!!!!
dans tous les cas trés bien Wiles.(j'attends jusqu'a demain la réponse de la troisième question mème de la part de ceux qui n'ont pas le droit de participer).

2- Puisque f (f (n))=n=>f est bijective.
D’où f (f (n+2) +2)=n=f (f (n)) => f (n+2) +2=f (n)
Comme f (1)=0 et f (0)=1 et par une petite récurrence on déduit que f (n)=1-n.

3- posons xy=a>0. Dans l’équation, il vient que f (f(x) +a/x)=xf (1+a).(*)
* f est surjective d’après (*).
*d’après (*) nous pouvons fixer a et changer x comme on veut (elle est monotone par suite). Cela nous amène à montrer que f est décroissante.
Supposons qu’elle croissante.
Soient 0<x<y et supposons que f(x) <f(y) => (f(x)-f(y))/ (1/x-1/y)>0.
Posons a= f(x)-f(y))/ (1/x-1/y)>0 => f(x) +a/x=f(y) +a/y => xf (1+a)=yf (1+a) (d’après (*)) => x=y .Contradiction donc f est décroissante.
* f est surjectif et monotone donc elle est continue.
* f est injective.
Si f(m)=f(n) => f(f(m)+y)=f(f(n)+y) => mf(1+my)=nf(1+ny).
Faisons f tendre vers 0 => mf (1)=nf (1) => m=n. D’où l’injectivité de f.
* posons x=1 => f (f (1) +y)=f (1+y) => f (1)=1.
* faisons y->0 dans l’initiale équation => f (f(x))=xf (1)=x
* posons y=1 => f(1+f(x))=xf(1+x)=f(x)f(1+f(x))=f(1+x) f(1+f(x))/x => f(x)=1/x pour tout x>0.
Réciproquement la fonction f(x)=1/x vérifie l’équation.
and we’re done.

quoique je ne vois vraiment pas ou est le probleme dans ma solution je vous proposerait cet exercice:

EXERCICE N° 48
resoudre dans R le systeme suivant:
x^3=2y-1
y^3=2z-1
z^3=2x-1
PS: desole pour ce retard due a mon etat de sante et a mon voyage.

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

x^3=2y-1 *
y^3=2z-1 **
z^3=2x-1 ***
*-**==> (x-y)(x²+y²+xy)=2(y-z)
alors signe(x-y)=sign(y-z) 1)
de mm on trouve 2) sign(x-z)=sign(y-x)
et 3)sign(y-z)=sin(z-x)
♣si on suppose x<y<z on a z-x>0 et y-z<0 alors 3) nest pas verifié .
♣si on suppsoe x..
..
on aboutit enfin a x=y=z
substutions dans lune des equations on trouve x^3-2x+1=0
==>x=1 ou x=(-1+rac(5))/2 ou x=- (1+rac(5))/2
(allah ychafik khay )

bien vu selfrespect tu pourras poster ton exo.

okey voila le mien :

EXERCICE N° 49
Soit ABC un triangle et AM la mediane issue de A :
montrer l'equivalence suivante :
AM=AB <===> sin(A)=2sin(B-C)

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

la mediane c'est almotawassit c ca?

BJR à Toutes et Tous !!!
Avec votre PERMISSION , je prends la liberté d’intervenir ici , seulement pour rappeler que Wiles est en droit total de considérer la propriété suivante , dépendante de l’entier NATUREL n et que j’énonce :
P(n) : pour tout relatif k , -n<=k<=n ; f(k)=1-k
IL EST VRAI qu’à l’intérieur elle implique des entiers relatifs , c’est cela l’ECONOMIE car on balayera Z tout entier , une fois qu’elle sera démontrée !!!!
Si on démontre par récurrence sur n que P(n) est vraie pour tout n ; alors on aura donc
f(k)=1-k qqque soit k dans Z
P(0) vraie : il faut vérifier que f(o)=1 ( QUI EST VRAIE PAR HYPOTHESE )
Supposons n>=1 et P(n) vraie alors montrons que P(n+1) est vraie ?????
Il suffira de vérifier que f(n+1)=1-n-1=-n et f(-n-1)=1+n+1 =2+n car on sait déjà selon l’hypothèse de récurrence que f(k)=1-k lorsque –n<=k<=n
Je pense pour ma part que la Démo proposée par Wiles peut etre considérée comme juste bien qu’elle ait besoin d’être remaniée et mise en forme , il a mis tous les ingrédients qu’il fallait .
A+
PS: Je parle ici du petit exo2) de l'EXERCICE47 de Redouane en page30 de ce Topic !!!!!

merci monsieur pour cette explication et j'espere que ma methode est plus claire maintenant.

je voudrait envoyer ma sol mais pour qu'elle soit plus claire il faut que j'insere une image le probleme c'est que je ne sait pas comment. Help

boukharfane radouane a écrit:

2- Puisque f (f (n))=n=>f est bijective.
D’où f (f (n+2) +2)=n=f (f (n)) => f (n+2) +2=f (n)
Comme f (1)=0 et f (0)=1 et par une petite récurrence on déduit que f (n)=1-n.

oui mais tu passe comment a Z ??

wiles a écrit:

je voudrait envoyer ma sol mais pour qu'elle soit plus claire il faut que j'insere une image le probleme c'est que je ne sait pas comment. Help

1.Tu clique sur "Insérer image"
2. Te voilà sur un hébergeur, tu crée un compte et puis t'ajoute ton image sur ce site "N'oublie pas la vérification d'extension"
3. Te voilà avec un lien qui comporte ton image
4. TU vien sur MathsMaroc on rédgant ton message, t'ecris le lien entre les balises Ton lien" border="0" alt=""/>

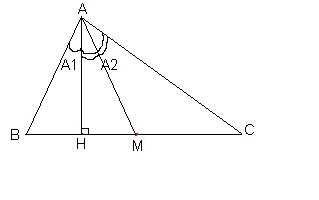soit H le projete hortogonal de A sur (BC)
puisque le triangle AMB est isocele et AH sa hauteur alors AH est aussi sa mediane donc BH=HM
alors HC=HM+MC=BH+BM=3BH

on sait que: sin(B-C)=sinBcosC-cosBsinC
=(AH/AB)*(HC/AC)-(BH/AB)*(AH/AC)
=2(AH*BH)/(AB*AC)
d'autre part on a: sinA=sin(A1+A2)
=sin(A1)cos(A2)+sin(A2)cos(A1)
=(BH/AB)*(AH/AC)+(HC/AC)*(AH/AB)
=4(AH*BH)/(AB*AC)
on conclut que 2sin(B-C)=sinA

meci codex ton truc marche a merveille