#Grand Jeu d'été (2007 ) TSM EST COMENCE ==>

wiles a écrit:

boukharfane radouane a écrit:

2- Puisque f (f (n))=n=>f est bijective.
D’où f (f (n+2) +2)=n=f (f (n)) => f (n+2) +2=f (n)
Comme f (1)=0 et f (0)=1 et par une petite récurrence on déduit que f (n)=1-n.

oui mais tu passe comment a Z ??

en fait si n app a N alors -n app a Z et la on peut deduire sur Z

saad007 a écrit:

wiles a écrit:

boukharfane radouane a écrit:

2- Puisque f (f (n))=n=>f est bijective.
D’où f (f (n+2) +2)=n=f (f (n)) => f (n+2) +2=f (n)
Comme f (1)=0 et f (0)=1 et par une petite récurrence on déduit que f (n)=1-n.

oui mais tu passe comment a Z ??

en fait si n app a N alors -n app a Z et la on peut deduire sur Z

ca ne donne rien

saad007 a écrit:

wiles a écrit:

boukharfane radouane a écrit:

2- Puisque f (f (n))=n=>f est bijective.
D’où f (f (n+2) +2)=n=f (f (n)) => f (n+2) +2=f (n)
Comme f (1)=0 et f (0)=1 et par une petite récurrence on déduit que f (n)=1-n.

oui mais tu passe comment a Z ??

en fait si n app a N alors -n app a Z et la on peut deduire sur Z

BJR à Toutes et Tous !!!
Cela ne passe pas aussi facilement , il faudra aussi établir que f(-n)=1+n lorsque n est dans IN pour être RIGOUREUX ! C'est toute la subtilité de la récurrence de Wiles qui englobe Z tout entier !!!!!!
A+

Oeil_de_Lynx a écrit:

BJR à Toutes et Tous !!!
Avec votre PERMISSION , je prends la liberté d’intervenir ici , seulement pour rappeler que Wiles est en droit total de considérer la propriété suivante , dépendante de l’entier NATUREL n et que j’énonce :
P(n) : pour tout relatif k , -n<=k<=n ; f(k)=1-k
IL EST VRAI qu’à l’intérieur elle implique des entiers relatifs , c’est cela l’ECONOMIE car on balayera Z tout entier , une fois qu’elle sera démontrée !!!!
Si on démontre par récurrence sur n que P(n) est vraie pour tout n ; alors on aura donc
f(k)=1-k qqque soit k dans Z
P(0) vraie : il faut vérifier que f(o)=1 ( QUI EST VRAIE PAR HYPOTHESE )
Supposons n>=1 et P(n) vraie alors montrons que P(n+1) est vraie ?????
Il suffira de vérifier que f(n+1)=1-n-1=-n et f(-n-1)=1+n+1 =2+n car on sait déjà selon l’hypothèse de récurrence que f(k)=1-k lorsque –n<=k<=n
Je pense pour ma part que la Démo proposée par Wiles peut etre considérée comme juste bien qu’elle ait besoin d’être remaniée et mise en forme , il a mis tous les ingrédients qu’il fallait .
A+

Salut Mr oeil de lynx ,
ben wiles a utilusé un raisonnemnt qui lui a permet daboutir a un resultat correct (mais la realité est que lareccuirence est dirigé pour montrer qu un resultat est juste par contre elle ne peut pas la trouver comme ça tt seule !! ) et remarquons aussi que wiles a pris comme base de reccurence n=0 qui etait presque trivial !! puis il a construit sa reccurence ce qui netait point securisé en fait il fallait se rappeler la fausse reccurence qui demontre que tt les points sont alignés (en fait si on prends n=2 pour ce resultat comme base : le raisonnement devient aprés 100/100 correct ) alors qu est ce qui vous fait assez sur que ce raisonnement est juste (ne dites pas le resultat , voyons le pb de la semaine 66 a eu pas mal de reponses qui aboutit au resultat juste mais ils etaient tous fausses )
merçi

BJR Selfrespect !!
On se retrouve en MP , c'est mieux pour ne pas polluer le Topic!
A tut

Oeil_de_Lynx a écrit:

BJR Selfrespect !!
On se retrouve en MP .
A tut

ok.
pour wiles :

wiles a écrit:

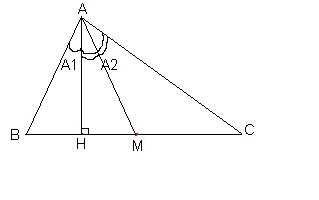
soit H le projete hortogonal de A sur (BC)
puisque le triangle AMB est isocele et AH sa hauteur alors AH est aussi sa mediane donc BH=HM
alors HC=HM+MC=BH+BM=3BH

on sait que: sin(B-C)=sinBcosC-cosBsinC
=(AH/AB)*(HC/AC)-(BH/AB)*(AH/AC)
=2(AH*BH)/(AB*AC)
d'autre part on a: sinA=sin(A1+A2)
=sin(A1)cos(A2)+sin(A2)cos(A1)
=(BH/AB)*(AH/AC)+(HC/AC)*(AH/AB)
=4(AH*BH)/(AB*AC)
on conclut que 2sin(B-C)=sinA

c juste wiles tas demontrés lequivalence en un seul depart .(tu peux aussi utiluser lidentité de la mediane .)
tu peux poster ton exo.

selfrespect a écrit:

c juste wiles tas demontrés lequivalence en un seul depart .(tu peux aussi utiluser lidentité de la mediane .)
tu peux poster ton exo.

d'accord.


EXERCICE N° 50
resoudre dans R le systeme suivant:
(x-1)(y^2+6)=y(x^2+1)
(y-1)(x^2+6)=x(y^2+1)

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

**(x-1)(y^2+6)=y(x^2+1)
* (y-1)(x^2+6)=x(y^2+1)
**-*==> (x-y)(x+y-2xy+7)=0
♣x=y ==>x=y=2 ou x=y=3
♣x+y+7-2xy=0
♠dautre part le systeme equivaut :
**(x-1)(y^2+6)=y(x^2+1)
* x(y^2+1)=(y-1)(x^2+6)
**-*==>(x+y)²-5(x+y)-2xy+12=0
==> (x+y)²-5(x+y)-(x+y)+5=0
==> (x+y)²-6(x+y)+5=0
==> x+y=5 ou x+y=1
==> (x+y=5 et xy=6 ) ou (x+y=1 et xy=4)
==> (x,y)£{(2,3),(3,2)}
reciproquemnt {(2,3),(3,2),(2,2),(3,3)} verifie le pb
S={(2,3),(3,2),(2,2),(3,3)}
merçi.

bien vu selfrespect
a toi mnt

okey voila mon exo : (geometrie )
EXERCICE N° 51

Soit ABC un triangle dont les cotés a,b,c demontrer que :
A=2B <==> a²=b(b+c)
A et B (des angles)
Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

selfrespect a écrit:

okey voila mon exo : (geometrie )

Soit ABC un triangle dont les cotés a,b,c demontrer que :
A=2B <==> a²=b(b+c)
A et B (des angles)
Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

a=[AB] et b= [AC] et c=[BC] c'est ça ou nn?

bonjour tt le monde
on a : sinB/b=sinA/a=sin(2B)/a=2sinBcosB/a
donc cosB=a/2b
d'apres AL-KACHY:
b^2=a^2+c^2-2ac*cosB
donc b^2-c^2=a^2-a^2c/b
alors: b(b+c)=a^2
pour demontrer l'autre sens il suffit de suivre les mm etapes a l'inverse.

wiles a écrit:

bonjour tt le monde
on a : sinB/b=sinA/a=sin(2B)/a=2sinBcosB/a
donc cosB=a/2b
d'apres AL-KACHY:
b^2=a^2+c^2-2ac*cosB
donc b^2-c^2=a^2-a^2c/b
alors: b(b+c)=a^2
pour demontrer l'autre sens il suffit de suivre les mm etapes a l'inverse.

Bonjour ,
je vais la considerr juste mais il ya juste un petit problem cest que :
dans lautre sens tu vas aboutir à sin(A)=sin(2B)
<==> A=2B ou pi-A=2B
comment tu vas ecarter le cas pi-A=2B

d'accord selfrespect.
puisque A+2B=pi donc B=C alors b=c
donc 2b^2=a^2 donc b^2+c^2=a^2
donc ABC est a la fois triangle rectangle et isocele
alors A=pi/2 et B=C=pi/4 alors a=2B

wiles a écrit:

d'accord selfrespect.
puisque A+2B=pi donc B=C alors b=c
donc 2b^2=a^2 donc b^2+c^2=a^2
donc ABC est a la fois triangle rectangle et isocele
alors A=pi/2 et B=C=pi/4 alors a=2B

Bravo wiles ,
tu peux poster ton exo .

EXERCICE N° 52
Resoudre l'equation fonctionnelle suivante:
f(xf(x)+f(y))=y+f(x)^2 (x et y de R)
enjoy

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

wiles a écrit:

peut on choisir l'un des signes + ou - devant chaque nombre pour obtenir l'egalite suivante?
(+-)100(+-)99(+-)98(+-)....(+-)3(+-)2(+-)1=1980
enjoy

slt je crois que jai deja envoyé un exo comme ça et je lai resolu alors si tu veux le changer je serai reconnaissant ( pour l'egalité b1sur)

d'accord
je le change

j'ai une solution :
on a: a^2+b^2+1/a^2 +b/a=a²+3/4a²+(b+1/2a)²
et on a:a²+3/4a²+(b+1/2a)²>= a²+3/4a²

et on a: a²+3/4a²>=V3

d'ou ^2+b^2+1/a^2 +b/a>=V3

fermat1988 a écrit:

j'ai une solution :
on a: a^2+b^2+1/a^2 +b/a=a²+3/4a²+(b+1/2a)²
et on a:a²+3/4a²+(b+1/2a)²>= a²+3/4a²

et on a: a²+3/4a²>=V3

d'ou ^2+b^2+1/a^2 +b/a>=V3

mais c'est la solution de quel exo??

ça commence probablement comme ceci. En faisant x=0, on voit que f(f(y)=y+f(0)^2=y+a pour tout y. En particulier, f est bijective, et il existe donc un u tel que f(u)=0. En posant x=u dans l'équation, il vient f(f(y))=y, donc a=0. Ce qui donne d'ailleurs f(0)^2=0, donc u=0.

Voilà, donc f est involutive 0 fixe. Les deux fonctions qui vérifient ça sont ±id, qui conviennent toutes les deux.

f involutive <==>fof=id

boukharfane radouane a écrit:

salut tout le monde.
voici seulement une autre démarche un peu détaillée.
*montrons que f est surjective
posons x=0 => f(f(y))=y+f²(0) ceq ui montre immédiatement l'injéctivité de f.
*montrons que f est injective
supposons que f(x)=f(y).
on a f(xf(x)+f(x))=y+f²(x) et f(xf(x)+f(x))=x+f²(x)
puisque f(xf(x)+f(y))=f(xf(x)+f(x)) => x=y.d'où la injéctivité de f.
on conclut que f est bijective.
*posons x=y=0 => f(f(0))=f²(0)).
et f(a)=0 =>a=0
d'où f(0)=0.
*posons x=0 =>f(f(y))=y.
*remplaçant x par f(x) =>f(xf(x)+f(y))=y+x²=y+f²(x)
d'où f²(x)=x² => f(x)=x où f(x)=-x.
réciproquement les deux fonctions obtenues vérifient l'équation.

bien redige tt est clair a part peut etre la couleur que t'as utilise
moi aussi j'ai fait la meme chose avec moins de details

chapeau mon ami

we je pense que la methode de RADOUANE est parfaite (je crois que celle de SAAD n'est pas totalement complete quoique juste la prochaine fois incha2alah ^^)
a toi radouane.
je demanderai par ailleurs a MR SAMIR de compter un point a notre ami saad puisque ca methode est juste mais manque de details