Grand Jeu d'Hiver TSM 2007-2008

on considerant la fonction f(x)=0 teque f(x)=nx+x^3-n
f est derivable sur R
f'(x)=n+3x²==>f est croissante sur [0;1] et f est continue donc il realise une bijection de [0;1]-------->[-n;1]
f(1)=1
f(0)=-n

on allique TVI pour trove qu'il existe un unique nombre telque f(x)=0

f(x_n)=0

nX_n+X^3_n=n

....................

Et l a 2eme ??

Alaoui.Omar a écrit:

C'est Bien Correcte Badr Sauf Une petite Remarque C'est le Cas Ou n=0 . Sauf ça Tout Est Bien Fait .Poste Ton Exercice Alors .
Merci

oui Omar il faut que n£N*

resoundre dans l'ensemble R l'equation suivante:



[;;]la partie entiere

Alors badr ??

d'apres lequation on aura sin(2x)=a avec a£{-1,0,1}
je vais etudier un cas et ça sera de même pour les autres
(si v svoulez je refais la démonstration)
sin(2x)=0
x=kpi/2
don [x²+3x-1]=0
[k²pi²/4 +3k*pi/2 -1]=0

donc k²pi²/4 +3k*pi/2 -1 est compris entre 0 (0 compris) et 1 ( 1 icompris)

donc on trouve les valeurs de k qui vérifient :
k²pi² + 6k*pi -4 est compris entre 0 et 4

on considere deux inequations
1-k²pi² + 6k*pi -4 positif
2-k²pi² + 6k*pi -8 négatif (j'ai soustrait 4)

onn prend k £ D=D1 inter D2

c a dire on resoud l'inequation d'inconnue k :
1- et 2-
ensuite on remplace les k pour trouver les x convenables


même chose pour les autres cas sin(2x)=1 et sin(2x)=-1

Nea® a écrit:

Alors badr ??

desole nea@ il a un problme de conexion

pose Fn(x)=nx+x^3-n

est calcule fn+1(x_n) inf a0

puis f(x_n+1) inf a f(x_n) f est croissant

d'ou la solution

Et pr la solution que j'ai postée ?

Salut Callo,
STP Continue Ta démonstration !Au Moins Pour 0 .
et C'est Si Possible Une Autre Fois Utilise Math-Type Ou Un Autre Programme D'écriture Mathématique.
Merci et A+

Est ce que Tu as Des Problèmes a Continuer Ta démonstration callo?

j'ai posté la methode il ne reste plus que des calculs (resolution des deux inequations)
et pr l'ecriture je vais essayer d'etre plus clair prochainement nshaalah
a+

Salut
Prouver que: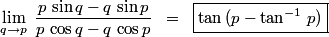



P.S:Les réponses doivent posté ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
-chaque réponse Lisible , correcte et Complète Vaut 2 points.
En cas de retard ou Triche .. le participant aura -2points


N.B:Essayer De Copier ce message dans chaque Poste D'exercice.

salut dsl de mon retard et a moi les -2 point car j 'avais des prob donc
on pose f(q)=psinq-qsinp et g(x)=pcosq-qcosp donc
lim(q->p) (f(q)-f(p))/(g(q)-g(p))=f'(p)/g'(p)
=(sinp-pcosp)/(cosp+psinp)=(tanp-p)/(1+ptanp)
=tan(arctan((tanp-p)/(1+ptanp)))
utilisant la relation de arctan(a)+arctanb=... on trouvra
tan(arctan(tanp)-arctanp)=tan(p-arctanp)
et a vous de poster l'exo a ma place et merci d'avance

kalm a écrit:

salut dsl de mon retard et a moi les -2 point car j 'avais des prob donc
on pose f(q)=psinq-qsinp et g(x)=pcosq-qcosp donc
lim(q->p) (f(q)-f(p))/(g(q)-g(p))=f'(p)/g'(p)
=(sinp-pcosp)/(cosp+psinp)=(tanp-p)/(1+ptanp)
=tan(arctan((tanp-p)/(1+ptanp)))
utilisant la relation de arctan(a)+arctanb=... on trouvra
tan(arctan(tanp)-arctanp)=tan(p-arctanp)
et a vous de poster l'exo a ma place et merci d'avance

Salut kAlm ,
Essaye de mieux eclaircir f(q) et f(p) Pareil pour g(p) et g(q).
A+

j rien a ajouter

est que le jeu d'hiver terminer ou quoi!!!§§!!!!§§

calculez la limite suivante

lim 1/1!+1/2!+1/3!+....+1/n!
n------>+00

badr a écrit:

calculez la limite suivante

lim 1/1!+1/2!+1/3!+....+1/n!
n------>+00

je crois que la limite cest :e-1

o0aminbe0o a écrit:

badr a écrit:

calculez la limite suivante

lim 1/1!+1/2!+1/3!+....+1/n!
n------>+00

je crois que la limite cest :e-1

des réponse que 'je crois ' ' peut étre' sans méthode n'ont pas admis dans ce jeu!!!!

Alaoui.Omar a écrit:

o0aminbe0o a écrit:

badr a écrit:

calculez la limite suivante

lim 1/1!+1/2!+1/3!+....+1/n!
n------>+00

je crois que la limite cest :e-1

des réponse que 'je crois ' ' peut étre' sans méthode n'ont pas admis dans ce jeu!!!!

http://fr.wikipedia.org/wiki/Exponentielle

voila tu trouveras ce que je tai dit pour la formule , mais la demo , je crois pas qu'elle puisse etre demontré par nos outils mathematiques

o0aminbe0o a écrit:

mais la demo , je crois pas qu'elle puisse etre demontré par nos outils mathematiques

siii

Fourrier-D.Blaine a écrit:

o0aminbe0o a écrit:

mais la demo , je crois pas qu'elle puisse etre demontré par nos outils mathematiques

siii

va voir page 233

vas y o0aminbe0o poste ton exercice puisque tu l'as trouvé (disant )