| | Grand jeu d'hiver pour les TC |  |
|
+13Rhitz Assaut-Graph -L- khawarizmi youna greatestsmaths h-o-u-s-s-a-m mhdi mathsformaths red11 girl-ambition.93 mathsmaster topmath 17 participants |
|
| Auteur | Message |
|---|
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 18:29 Ven 19 Sep 2008, 18:29 | |
| l inégalité équivaut
(a-b)²+(b-c)²+(c-a)²+(a-1/2)²+(b-1/2)²+(c-1/2)²>=0
ce qui est vrai
Dernière édition par h-o-u-s-s-a-m le Ven 19 Sep 2008, 18:34, édité 1 fois | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 18:32 Ven 19 Sep 2008, 18:32 | |
| voila qlq chose de plus simple:
on a:
(a+b-c)²+1/4>=a+b-c
de mm pour les autres puis deduir l'inegalité demandé. | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 18:33 Ven 19 Sep 2008, 18:33 | |
| | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 21:28 Ven 19 Sep 2008, 21:28 | |
| 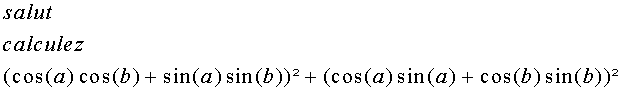 facile | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 21:58 Ven 19 Sep 2008, 21:58 | |
| elle donne une valeur numérique houssam ou non | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 22:04 Ven 19 Sep 2008, 22:04 | |
| | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 22:20 Ven 19 Sep 2008, 22:20 | |
| tu es sur de l'exo car j'ai utiliser les formules trigo sur eux mais ça rien de chiffre stp vérifie si l'exo est juste si tu as fait une faute de frappe | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 22:37 Ven 19 Sep 2008, 22:37 | |
| a dsl c est plutot
(cos(a)cos(b)-sin(a)sin(b))²+(sin(a)cos(b)+cos(a)sin(b))² | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 22:53 Ven 19 Sep 2008, 22:53 | |
| maintenat c facile:
S=cos²(a)cos²(b)+sin²(a)sin²(b)+sin²(a)cos²(b)+cos²(a)sin²(b)=cos²(a)(cos²(b)+sin²(b))+sin²(a)(cos²(b)+sin²(b))=1 | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 22:58 Ven 19 Sep 2008, 22:58 | |
| je pense que t'es dans la fausse route
S=cos²(a)cos²(b)+sin²(a)sin²(b)+sin²(a)cos²(b)+cos²(a)sin²(b)
comment t'as fait?
en plus dans l'exo de houssam la deuxieme partite il y a
cos(a)sin(a) non pas cos(a)sin(b) | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 23:51 Ven 19 Sep 2008, 23:51 | |
| - mathsformaths a écrit:
- je pense que t'es dans la fausse route
S=cos²(a)cos²(b)+sin²(a)sin²(b)+sin²(a)cos²(b)+cos²(a)sin²(b)
comment t'as fait?
en plus dans l'exo de houssam la deuxieme partite il y a
cos(a)sin(a) non pas cos(a)sin(b) il a fait comme ça S=cos²(a)cos²(b)+sin²(a)sin²(b)+2sin(a)cos(a)sin(b)cos(b)+sin²(a)cos²(b)+cos²(a)sin²(b)-2sin(a)cos(a)sin(b)cos(b) | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Ven 19 Sep 2008, 23:53 Ven 19 Sep 2008, 23:53 | |
| poste ton exo mathsmaster | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 10:35 Sam 20 Sep 2008, 10:35 | |
| c'est simplement faux car qu'on calcule on trouve 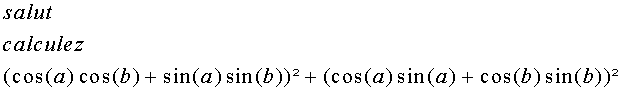 S=cos²(a)cos²(b)+sin²(a)sin²(b)+2sin(a)cos(a)sin(b)cos(b)+sin²(a)cos²(a)+cos²(a)sin²(a)+2sin^2(a)cos^2(a) regardez l'exo bien c'est pourquoi j'ai dis qu'il faut le changer ou le corriger . | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:27 Sam 20 Sep 2008, 12:27 | |
| - h-o-u-s-s-a-m a écrit:
- a dsl c est plutot
(cos(a)cos(b)-sin(a)sin(b))²+(sin(a)cos(b)+cos(a)sin(b))² rah je l ai corriger hier | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:36 Sam 20 Sep 2008, 12:36 | |
| ah je l'ai pas vu tu devais le corriger dans le poste d'origine
je l'ai fait deja c simple.
jai perdu 2 pt en l'air c'est pas grave | |
|
  | |
mathsmaster
Expert sup

 Nombre de messages : 1500 Nombre de messages : 1500
Age : 31
Localisation : chez moi.
Date d'inscription : 06/02/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:41 Sam 20 Sep 2008, 12:41 | |
| sachant que: x,y,z>=1 et 1/x+1/y+1/z=2. prouver que:
 iwa jawbo daba ou postiw daba.
Dernière édition par mathsmaster le Sam 20 Sep 2008, 12:50, édité 1 fois | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:45 Sam 20 Sep 2008, 12:45 | |
| qu'est ce qu'on prouve il n ' ya pas de question juste des propositions | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:52 Sam 20 Sep 2008, 12:52 | |
| non mon explorateur ne presentez pas les images dsl | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:54 Sam 20 Sep 2008, 12:54 | |
| | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 12:58 Sam 20 Sep 2008, 12:58 | |
| Determiner le maximum valeur réelle possible du nombre  , tel que:  pour tous les réels tels que  avec  | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 13:23 Sam 20 Sep 2008, 13:23 | |
| K dois avoir une valeure numérique? | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 13:25 Sam 20 Sep 2008, 13:25 | |
| | |
|
  | |
mathsformaths
Maître
 Nombre de messages : 131 Nombre de messages : 131
Age : 31
Date d'inscription : 21/07/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 13:26 Sam 20 Sep 2008, 13:26 | |
| si vous ne trouver pas la solution je vous donnere la valeur de k puis je vous laisse travailler dessus comme une inégalité
je vous laisse jusqu'au 17h | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 14:06 Sam 20 Sep 2008, 14:06 | |
| salut
je suis pas sur mais bon
on met: p=a+b+c ;q=ab+ac+bc;r=abcet p=q
l inégalité équivaut
p(p²+q)/(pq-r)>=k(p+1)
p²(p+1)>=k(p+1)(pq-r)
(p+1)(p²-kp²+kr)>=0
(p²(1-k)+rk)>=0 il se peut que l une des variables =0 alors r=0
p²(1-k)>=0==>k=1 | |
|
  | |
h-o-u-s-s-a-m
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 31
Date d'inscription : 21/06/2008
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  Sam 20 Sep 2008, 14:27 Sam 20 Sep 2008, 14:27 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Grand jeu d'hiver pour les TC Sujet: Re: Grand jeu d'hiver pour les TC  | |
| |
|
  | |
| | Grand jeu d'hiver pour les TC |  |
|
