Préparations aux olympiades de tronc commun (2009-2010)

ABC est un triangle rectangle en A.
ABH et AHC sont deux triangles rectangles en H.
H1 est le rayon du cercle inscrit au triangle ABH.
H2 est le rayon du cercle inscrit au triangle AHC.
E est le milieu de [AB], et F de [AC]
Montrez que :

E et F sont-elles les milieux respectifs de AB et AC?

nmo a écrit:

E et F sont-elles les milieux respectifs de AB et AC?

Effectivement ! C'est édité

Il est clair que H1+EH>=BH et que H2+FH>=CH.
Donc (H1+EH)(H2+FH)>=BH*CH==>(¤), car tout est positif.
D'autre part en appliquant le téorème de pytagore sur
# le triangle ABC on a AB^2+AC^2=BC^2.==>(1)
# le triangle ABH on a AH^2+BH^2=AB^2.==>(2)
# le triangle ACH on a HC^2+AH^2=AC^2.==>(3)
Et on remplaçons 2 et 3 dans 1 on trouve AH^2+BH^2+HC^2+AH^2=BC^2.
Donc 2AH^2+BH^2+CH^2=(BH+HC)^2.
Donc 2AH^2+BH^2+CH^2=BH^2+CH^2+2BH*CH.
Donc 2AH^2=2BH*CH.
Finalement AH^2=BH*CH.
Et en remplaçant dans ¤ on trouve (H1+EH)(H2+FH)>=AH^2.
J'espère qu'il soit juste. (En attente de vos confirmation.)

nmo a écrit:

Il est clair que H1+EH>=BH et que H2+FH>=CH.

Vraiment ? Peux-tu le prouver ?

Pour terminer la démonstration:
On a ABH un triangle rectangle en H.
Donc 2AE>BH.
Donc 2EH>BH.
D'autre part 2H1>BH.
En sommant 2H1+2EH>=2BH.
Soit en résumé H1+EH>=BH.
On procède de la même manière pour démontrer que H2+FH>=CH.
J'attend ta confirmation Dijkschneier.

nmo a écrit:

D'autre part 2H1>BH.

Vraiment ? Peux-tu le prouver ?

Dijkschneier a écrit:

nmo a écrit:

D'autre part 2H1>BH.

Vraiment ? Peux-tu le prouver ?

Oui, c'est une faute d'inattention que je vais rectifier.

Pour terminer ma première démonstration:
Soit O le centre du cercle inscrit au triangle ABH.
Soit T la projection orthogonale de O sur AB.
On pose AT=e et BT=f et H1=r.
Il est facile de démontre que AH=e+r et que BH=f+r.
Sur la figure, on a e>=f.
Donc e+f>=2f.
Donc 1/2(e+f)>=f.
Donc 1/2(e+f)+r>=f+r.
Finalement (1/2)AB+H1>BH.
Il s'ensuit que EH+H1>BH.
On procède de la même manière pour démontrer que H2+FH>=CH.
J'attend ta confirmation Dijkschneier.

Tes identités sont réellement saugrenues.

nmo a écrit:

Il est facile de démontre que AH=e+r et que BH=f+r.

Pourquoi, par exemple ?

C'est juste, mais sa démonstration est longue.
Je vais la poster dès qu'elle soit rédigée.

C'est juste, et voici sa démonstration:
Soit O le centre du cercle inscrit au triangle ABH.
Soit U et V les projections orthogonales respectifs de O sur AH et BH.
On a U et T sont deux points du cercle
Et par conséquent OT=OU=r ==>(1).
Et comme O est le centre du cercle inscrit au triangle ABH
On a O appartient au bissectrice de l'angle BAH.
Donc AO est au bissectrice de l'angle TAU
Donc OAU=OAT (angles).
Et on sait que OUA=OTA (angles).
On sait que la sommes des angles d'un triangle vaut 180°.
Donc 180°=OUA+UAO+AOU=OTA+TAO+AOT (angles).
En utilisant ce qui précéde on trouve AOU=AOT (angles).==>(2).
Et comme CO un côté commun entre les triangles AOT et AOU et en utilisant 1 et 2,
Il s'ensuit que les triangles AOT et AOU sont égaux.
Donc leurs côtés juxtaposés sont égaux, et par la suite:
AU=AT=e.==>(a)
Même méthode pour démontrer que BV=BT=f.==>(b)
D'après les données que j'ai annoncé, on a AH est perpendiculaire sur OU.
Et on a AH est perpendiculaire sur BH.
Il s'ensuit que OU est parallèle avec BH.
Et comme on a AHB=HUU=HVO=90°.
On déduit que HUOV est un carré.
Par conséquent OU=OV=VH=HU=r.==>(c)
En utilisant a et c on a AH=AU+UH=e+r.
Et b et c on a BH=BV+VH=f+r.
Sauf erreur bien sûr.

nmo a écrit:

C'est juste, et voici sa démonstration:
Soit O le centre du cercle inscrit au triangle ABH.
Soit U et V les projections orthogonales respectifs de O sur AH et BH.
On a U et T sont deux points du cercle
Et par conséquent OT=OU=r ==>(1).
Et comme O est le centre du cercle inscrit au triangle ABH
On a O appartient au bissectrice de l'angle BAH.
Donc AO est au bissectrice de l'angle TAU
Donc OAU=OAT (angles).
Et on sait que OUA=OTA (angles).
On sait que la sommes des angles d'un triangle vaut 180°.
Donc 180°=OUA+UAO+AOU=OTA+TAO+AOT (angles).
En utilisant ce qui précéde on trouve AOU=AOT (angles).==>(2).
Et comme CO un côté commun entre les triangles AOT et AOU et en utilisant 1 et 2,
Il s'ensuit que les triangles AOT et AOU sont égaux.
Donc leurs côtés juxtaposés sont égaux, et par la suite:
AU=AT=e.==>(a)
Même méthode pour démontrer que BV=BT=f.==>(b)
D'après les données que j'ai annoncé, on a AH est perpendiculaire sur OU.
Et on a AH est perpendiculaire sur BH.
Il s'ensuit que OU est parallèle avec BH.
Et comme on a AHB=HUU=HVO=90°.
On déduit que HUOV est un carré.
Par conséquent OU=OV=VH=HU=r.==>(c)
En utilisant a et c on a AH=AU+UH=e+r.
Et b et c on a BH=BV+VH=f+r.
Sauf erreur bien sûr.

Celle-là, je te l'accorde !
Mais revenons à ça :

Citation :

Pour terminer ma première démonstration:
Soit O le centre du cercle inscrit au triangle ABH.
Soit T la projection orthogonale de O sur AB.
On pose AT=e et BT=f et H1=r.
Il est facile de démontre que AH=e+r et que BH=f+r.
Sur la figure, on a e>=f.
Donc e+f>=2f.
Donc 1/2(e+f)>=f.
Donc 1/2(e+f)+r>=f+r.
Finalement (1/2)AB+H1>BH.
Il s'ensuit que EH+H1>BH.
On procède de la même manière pour démontrer que H2+FH>=CH.
J'attend ta confirmation Dijkschneier.

Si tu supposes en premier que , serait-il toujours possible de faire de même dans le triangle AHC ? Le mieux serait d'apporter une preuve rigoureuse à cela !

Ma démonstration est-elle comptée juste?
Puis-je poster un exercice?

nmo a écrit:

Ma démonstration est-elle comptée juste?

Pas vraiment. Essaie de changer d'optique.

Si tu n'as pas donné l'exercice accompagné de la figure, il faut que je suppose que e>=f.
Mais sur la figure, on a clairment e>=f.
Même cela, on peut verser e avec f dans la démonstration au cas ou f>=e.

Je suis d'accord que , d'après la figure.
Mais alors, qu'en diras-tu dans le triangle AHC ?

Citation :

On procède de la même manière pour démontrer que H2+FH>=CH.

J'aimerais bien justement que tu termines ta preuve.

Il suffit de prendre A=C, H=H, et B=A, et tu connais le reste.

pr l'exo 2 voir:
https://mathsmaroc.jeun.fr/seconde-tronc-commun-f6/exo-de-math-d-t15068.htm

Le problème courant est le voici:
a,b,c sont les trois cotés d'un triangle tel que a^3+b^3+c^3=3abc.
Quel est sa nature?
Bonne chance.

Solution au problème précédent :

Solution au problème courant :
a,b et c étant les longueurs de côtés d'un triangle, ils sont strictement positifs.
Ainsi, d'après l'IAG, l'on a avec égalité si et seulement si 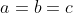, i.e, lorsque le triangle est équilatéral.

Pour ta première solution, le mot "excellent" est le seul à dire.
Pour le deuxième, voici ce que j'ai fait:
En développant l'expres​sion(a+b+c)(a^2+b^2+c^2-ab-ac-bc) on trouve a^3+b^3+c^3-3abc.
On a a^3+b^3+c^3=3abc.
Donc a^3+b^3+c^3-3abc=0.
Donc (a+b+c)(a^2+b^2+c^2-ab-ac-bc)=0.
Donc (1/2)(a+b+c)(2a^2+2b^2+2c^2-2ab-2ac-2bc)=0.
Donc (1/2)(a+b+c)(a^2-2ab+b^2+c^2-2ac+a^2+b^2-2bc+c^2)=0.
Donc (1/2)(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]=0.
Et puisque 1/2#0 et a+b+c#0.
On a [(a-b)^2+(b-c)^2+(c-a)^2]=0.
Donc (a-b)^2=0 et (b-c)^2=0 et (c-a)^2=0.
Donc a-b=0 et b-c=0 et c-a=0.
Donc a=b et b=c et c=a.
Donc a=b=c.
Finalement le triangle est équilatéral comme tu as trouvé.
Donc, tu as l'honneur d'accélérer notre jeu avec un nouveau exercice.

En attente toujours Dijkschneier, poste un nouveau exercice.

Problème 1 :
ABC est un triangle et I le milieu de [AB].
M et N sont deux points tels que : et ; .
J est le milieu de [MN].
Montrer que .
Problème 2 :
ABCD est un quadrilatère convexe. A', B', C', et D' sont des points tels que :
.
Montrer que l'aire du quadrilatère A'B'C'D' est égale à cinq fois l'aire du quadrilatère ABCD.

Problème 1 :
j'ai bien aimé voila ce que j'ai fais :
soit N' un point tel que : V(N'A)=kV(N'C) V(vecteurs
soit M' un point similaire !
puisque V(NA)=-V(N'A) et V(M'B)=-V(MA)

on peut appliquer Thalès et on trouvera :
que les segment NM' et MN' sont parallèles à BC
on en déduit aussi que I est le milieu de MM' et que V est le milieu de NN' ( V étant le milieu de AC)
soit J' le milieu de N'M' en utilisant Thalès On peut prouver que JJ' est parallèle a MN et de ce fait parallèle a BC et puisque I,J,J',V sont alignés . Le résultats s'en suit .... C'est une solution assez longue et compliqué je pense qu'il existe une solution plus facile ( barycentre par exemple mais ce n'est pas du niveau tronc commun )

Pour le deuxiéme :
Je pense qu'on vas utilisé la règle de l'aire d'un quadrilatère convexe , enfin je ne suis pas sûr mais il suffirait de trouvé la longueur des diagonales de A'B'C'D' en les écrivant sous forme des segments d'ABCD !! J'essayerai demain ... sur ce bonne nuit