polynomes

démontrez que pourtout entier n>=2; le polynome f(x)=((x+1)^2n)-(x^2n)-2x-1
est divisible par x(x+1)(2x+1)
en cas de reponse postez vos exercices.

voici un autre exercice:
-Resoudre dans R^2 les équations suivantes:
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
x-1=0

sinn faut juste calculer:
P(O) ; P(-1) : P(-1/2)

calculez la donc. et puis c'est f(x) non pas P(x).

P(x)=((x+1)^2n)-(x^2n)-2x-1
P(0)=1^2n-0^2n-0-1=0
P(-1)=0^2n-(-1)^2n+2-1=2-2=0
P(-1/2)=(-1/2)^2n-(-1/2)^2n+1-1=0
donc x l P(x) et x-1 l P(x) et x+1/2 l P(x)
ces polynomes sont irréductibles donc leurs produit divise P(x)

Je veux des exercices d'olympiades pour mieux préparer pour la seconde étape. Et merci d'avance.
voici un exercice de ma part:
soient a,a',a",b,b',b" des réels tel que: a/b<a'/b'<a"/b"
montrer que: a/b<(ab+a'b'+a"b")/(b^2+b'^2+b"^2)<a"/b"

louis a écrit:

voici un autre exercice:
-Resoudre dans R^2 les équations suivantes:
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
x-1=0

Pour la première voilà ma réponse:
On a (x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0.
Donc (x^2+y^2-4)^2*(xy-1)^2=0 et V(y^2+x^2)=0.
Donc (x^2+y^2-4)(xy-1)=0 et y^2+x^2=0.
De l'équation y^2+x^2=0 On tire x=y=0.
Ce qui n'affectue pas la deuxième équation et il en résulte que l'ensemble vide est la solution de cette équation.
Et pour la deuxième:
On a x-1=0
Donc x+0y-1=0
Donc x=1-0y.
Donc l'ensemble des solution est (1-0y,y)/ y appartient a l'ensemble R.
J'attends vos confirmations.

nmo a écrit:

louis a écrit:

voici un autre exercice:
-Resoudre dans R^2 les équations suivantes:
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
x-1=0

Pour la première voilà ma réponse:
On a (x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0.
Donc (x^2+y^2-4)^2*(xy-1)^2=0 et V(y^2+x^2)=0.
Donc (x^2+y^2-4)(xy-1)=0 et y^2+x^2=0.
De l'équation y^2+x^2=0 On tire x=y=0.
Ce qui n'affectue pas la deuxième équation et il en résulte que l'ensemble vide est la solution de cette équation.
Et pour la deuxième:
On a x-1=0
Donc x+0y-1=0
Donc x=1-0y.
Donc l'ensemble des solution est (1-0y,y)/ y appartient a l'ensemble R.
J'attends vos confirmations.

Pas forcément dsl ^^

si a>=0 et b>=0
et a+b=0 ==> a=< 0 et b=<0
==> a=0 et b =0
inversement 0+0=0

louis a écrit:

Je veux des exercices d'olympiades pour mieux préparer pour la seconde étape. Et merci d'avance.
voici un exercice de ma part:
soient a,a',a",b,b',b" des réels tel que: a/b<a'/b'<a"/b"
montrer que: a/b<(ab+a'b'+a"b")/(b^2+b'^2+b"^2)<a"/b"

il reste celui-là.

mais où-êtes vous? J'attends vos exercices et vos reponses.

si non; je vais vous donné un prochainement.

nmo a écrit:

louis a écrit:

voici un autre exercice:
-Resoudre dans R^2 les équations suivantes:
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
x-1=0

Pour la première voilà ma réponse:
On a (x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0.
Donc (x^2+y^2-4)^2*(xy-1)^2=0 et V(y^2+x^2)=0.
Donc (x^2+y^2-4)(xy-1)=0 et y^2+x^2=0.
De l'équation y^2+x^2=0 On tire x=y=0.
Ce qui n'affectue pas la deuxième équation et il en résulte que l'ensemble vide est la solution de cette équation.
Et pour la deuxième:
On a x-1=0
Donc x+0y-1=0
Donc x=1-0y.
Donc l'ensemble des solution est (1-0y,y)/ y appartient a l'ensemble R.
J'attends vos confirmations.

On écrit cela juste lorsqu'on a a*b=0 mais si c'est a+b=0 c'est faux car ça peut être deux nombres opposés mais pour a*b=0 forcément l'un des deux cotés est nul. ^^

Sinon j'ai essayé mais je sais pas si c'est vrai :p
on a x-1=0 du coup x=1
On remplace
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
(1+y²-4)²*(y-1)²+V(y²+1)=0
.....

Si on a x^2+y^2=0.
Avec x^2>=0 et y^2>=0.
Donc x^2=-y^2.
Et comme on a x^2>=0.
Cela veut dire -y^2>=0.
Ensuite y^2=<0.
Et on sait que y^2>=0.
De ce fait y^2=0.
Il s'ensuit que x^2=0.
Conclusion si a+b=0 et a>=0 et b>=0.
On a forcément: a=b=0.
Ce qui veut dire que ma solution est juste.
Pour soumitous la première équation est séparée de la deuxième.

soumitous a écrit:

Sinon j'ai essayé mais je sais pas si c'est vrai :p
on a x-1=0 du coup x=1
On remplace
(x^2+y^2-4)^2*(xy-1)^2+V(y^2+x^2)=0
(1+y²-4)²*(y-1)²+V(y²+1)=0
.....

Premièrement ce n'est pas un système.

Voilà un autre exercice:
1/Démontrez que pour tous réel x>=3, on a: [x/(x^2-x-1]=<[x]/2
2/résolvez dans R (x^3+2x^2-16x-14)/(2x+1)=<x-2.
JE VEUX LA RéPONSE AVEC UN EXERCICE DANS LE PLUS PROCHE DELAI(je vous donne une semaine).

1/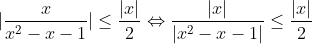

|x| étant strictement positif, on peut multiplier par 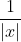sans changer le sens de l'inégalité :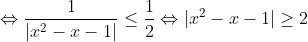

La dernière équivalence est vraie du fait que les nombres sont positifs.
Mais on a alors :

D'où : 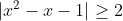, ce qui clôt la démonstration.
Le cas d'égalité n'a de plus jamais lieu.

2/


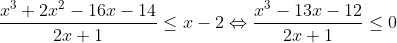Le tableau des signes montre alors que :

PS : les parenthèses ont repris la place des crochets, car ceux-ci ne semblent pas marcher sur ce forum.

Tu as oublié le carrée de 2x^2 dans le second exercice.
Quant au premier c'est juste.

Je veux la méthode des TC.
Je veux aussi des exercices des olympiades précédents des TC.
Les olympiades sont proche(le mois de février).
Et merci.

voici un exercice de ma part:
soit a,b,c les longueurs d'un triangle S sa surface et p son demi périmètre.
Prouvez que: S=V[p(p-a)(p-b)(p-c)]

louis a écrit:

voici un exercice de ma part:
soit a,b,c les longueurs d'un triangle S sa surface et p son demi périmètre.
Prouvez que: S=V[p(p-a)(p-b)(p-c)]

la formule de Héron ....

majdouline a écrit:

louis a écrit:

voici un exercice de ma part:
soit a,b,c les longueurs d'un triangle S sa surface et p son demi périmètre.
Prouvez que: S=V[p(p-a)(p-b)(p-c)]

la formule de Héron ....

Je sais que c'est la formule de Héron mais je veux sa démonstration.