polynomes

M.Marjani a écrit:

Un EX à vous :

.

Bonne chance

C'est un exercice très facile, zouhair a fait l'affaire.
Donc c'est à lui de poster un nouveau exercice.

zouhir a écrit:

oui mais c'est facile il faut juste

Oui c'est la bonne idée , à vous de posez ))

nmo a écrit:

La solution de mon exercice:
On a a, b, et c des longueurs des côtés d'un triagle.
Donc, d'après l'inégalité triangulaire, a<b+c.
Donc a+a<a+b+c.
Donc 2a<1.
Donc a<1/2.
De même b<1/2.
Et c<1/2.
Posons maintenant a=1/2-x, b=1/2-y, et c=1/2-z.
On a a<1/2 et b<1/2 et c<1/2.
Donc 0<1/2-a et 0<1/2-b et 0<1/2-c.
Donc 0<1/2-(1/2-x) et 0<1/2-(1/2-y) et 0<1/2-(1/2-z).
Donc 0<1/2-1/2+x et 0<1/2-1/2+y et 0<1/2-1/2+z.
Donc 0<x et 0<y et 0<z.
Et on a a+b+c=1.
Donc 1/2-x+1/2-y+1/2-z=1.
Donc 1/2=x+y+z.
D'autre part, on fait la soustraction a²+b²+c²+4abc-1/2=(1/2-x)²+(1/2-y)²+(1/2-z)²+4(1/2-x)(1/2-y)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=1/4-2*1/2*x+x²+1/4-2*1/2*y+y²+1/4-2*1/2*z+z²+4(1/4-1/2*y-1/2*x+xy)(1/2-z)-1/2.
Donc a²+b²+c²+4abc-1/2=3/4-1/2-x+x²-y+y²-z+z²+4(1/8-1/4*z-1/4*y+1/2*yz-1/4*x+1/2*xz+1/2*xy-xyz).
Donc a²+b²+c²+4abc-1/2=1/4-(x+y+z)+x²+y²+z²+1/2-z-y+2yz-x+2xz+2xy-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4-1/2+(x²+y²+z²+2xy+2xz+2yz)+1/2-(x+y+z)-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(x+y+z)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+(1/2)²-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/4+1/4-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=1/2-1/2-4xyz.
Donc a²+b²+c²+4abc-1/2=-4xyz.
On a déja démontré que 0<x et 0<y et 0<z.
Donc 0<xyz.
Donc -4xyz<0.
Donc a²+b²+c²+4abc-1/2<0.
Donc a²+b²+c²+4abc<1/2.
CQFD.
Sauf faute de frappe.

Bonne idée nmo , t'as parti pour démontré que a²+b²+c²+4abc-1/2<0
Ca serait trés bien si tu peux effacer ou bien réduire quelques étapes , je veux dire quelques étapes tu peux les faire en utilisant l'observation sans les écrire.

J'ai bien aimé votre methode. Bonne chance.

Problème proposé:
Calculez sin x et cos x sachant que l'on a 3sin x +4cos x=5.
Puis déduisez la valeur de x à l'aide de la calculatrice.
Bonne chance.

Si ;
Il est connu que , et donc, , car 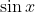est positif.
L'équation devient équivalente à :
car , et donc, l'équation équivaut à :
Posant avec , l'équation devient :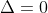
, , , .
Si ;
.
L'équation devient équivalente à :
Mais , donc pas de solutions dans ce cas.

De fait, , et x vaut approximativement 0.64 dans [0,PI].

nmo a écrit:

Problème proposé:
Calculez sin x et cos x sachant que l'on a 3sin x +4cos x=5.
Puis déduisez la valeur de x à l'aide de la calculatrice.
Bonne chance.

Posons tel que puisque
Nous avons donc
Puisque
Alors :
Sauf erreur.
Je sais, je n'ai pas vraiment répondu à la question mais bon, cette méthode peut toujours servir.
Au plaisir ! =)

mizmaz a écrit:

Posons tel que puisque
Nous avons donc
Puisque
Alors :
Sauf erreur.
Je sais, je n'ai pas vraiment répondu à la question mais bon, cette méthode peut toujours servir.
Au plaisir ! =)

Joli ! Pour agrémenter le tout, tu pouvais conclure en retournant les valeurs de sin(x) et de cos(x), une fois le x déterminé.

Dijkschneier a écrit:

mizmaz a écrit:

Posons tel que puisque
Nous avons donc
Puisque
Alors :
Sauf erreur.
Je sais, je n'ai pas vraiment répondu à la question mais bon, cette méthode peut toujours servir.
Au plaisir ! =)

Joli ! Pour agrémenter le tout, tu pouvais conclure en retournant les valeurs de sin(x) et de cos(x), une fois le x déterminé.

Merci et effectivement, j'aurais pu faire cela. Mais vu l'ordre dans lequel les choses ont été demandées, ça aurait ressemblé sans doute à une esquive.

Nous avons
D'autre part on a
Donc
Donc
Donc
Donc
Donc
Donc
Donc
De là, on trouve avec la formule de l'énoncé:
Donc
Enfin avec une calculatrice, on trouve:

Voici deux exercices proposés:
le premier:
ABCD est un carré. tels qu'on ait (EG) orthogonale à (FH).
1- Soit I l'intersection de (EG) et (BC) et J celle de (FH) et (AB).
Montrer que (EF) et (IJ) sont orthogonales.
2- Comment choisir (EG) et (FH) pour que EFGH soit un carré.
le deuxième:
Résoudre dans l'équation suivante:
P.S:ce qui répond poste un exercice avec sa réponse.

louis a écrit:

Voici deux exercices proposés:
le premier:
ABCD est un carré. tels qu'on ait (EG) orthogonale à (FH).
1- Soit I l'intersection de (EG) et (BC) et J celle de (FH) et (AB).
Montrer que (EF) et (IJ) sont orthogonales.
2- Comment choisir (EG) et (FH) pour que EFGH soit un carré.
le deuxième:
Résoudre dans l'équation suivante:
P.S:ce qui répond poste un exercice avec sa réponse.

C'est facile quand-même, réflichissez un peux.

Voici la réponse de la première question du premier exercice:
Il faut considérer les hauteurs du triangle EIJ.(AB) ET (BC) sont perpendiculaires, ce qui fait de (BI) une hauteur de EIJ. (EG) et (HF) sont perpendiculaires, donc (EI) et (FJ) sont perpendiculaires et (FJ) est une deuxième hauteur de EIJ. Sachant que (BI) et (FJ) se coupe en F, F est l'orthocentre de EIJ, et donc (EF), hauteur, est perpendiculaire à (IJ).
Je vais poster toutes les réponses après.

Bon voici une petite soluce du deuxiéme EX :
Premiérement on a :
Df= [1,+00]U[-00,-1]
V(x²-1)-V(x-1)=0
=> x²-x=0 => x=1 Ou x=0
On annule le 0 car x>=1,x=<-1
=> S={1}

A vous de postez.

M.Marjani a écrit:

Bon voici une petite soluce du deuxiéme EX :
Premiérement on a :
Df= [1,+00]U[-00,-1]
V(x²-1)-V(x-1)=0
=> x²-x=0 => x=1 Ou x=0
On annule le 0 car x>=1,x=<-1
=> S={1}

A vous de postez.

Ne jamais fermer l'intervalle en .
Au plaisir !

mizmaz a écrit:

M.Marjani a écrit:

Bon voici une petite soluce du deuxiéme EX :
Premiérement on a :
Df= [1,+00[U]-00,-1]
V(x²-1)-V(x-1)=0
=> x²-x=0 => x=1 Ou x=0
On annule le 0 car x>=1,x=<-1
=> S={1}

A vous de postez.

Ne jamais fermer l'intervalle en .
Au plaisir !

Faute de frappe

Résolvez en IR l'inéquation suivante:
.
Bonne chance.

mizmaz a écrit:

nmo a écrit:

Résolvez en IR l'inéquation suivante:
.
Bonne chance.

Good man.
Une autre Exo

Soit f une fonction définie de IR vers IR, tel que 5f(-x)+f(1-x)=2x.
Exprimez f(x) en fonction de x.
Bonne chance.

On a: 5f(-x)+f(1-x)=2x (1) , donc: 5f(x)+f(1+x)=-2x (4)
Posons dans l'égalité (1) x=x+1 on trouve que: 5f(-x-1)+f(-x)=2(x+1) (2)
(1)+(2)=> 6f(-x)+f(1-x)+5f(-x-1)=2(2x+1) =>6f(x)+f(1+x)+5f(x-1)=2(-2x+1) (3)
(3)-(4)=> f(x)+5f(x-1)=2(-3x+1) (A)
(3)-(A)=> 5f(x)+f(1+x)=2(-2x+1)-2(-3x+1)=2x
Donc: 2x=5f(x)+f(1+x)=5f(-x)+f(1-x) => f(x)=f(-x)
On a: 5f(x+1)+f(x)=2(x+1) et 5f(x)+f(1+x)=-2x
En additionant => 6f(x)+6f(1+x)=2
f(x)+f(1+x)=1/3 (1)
5f(x)+f(1+x)=2x (2)
(2)-(1) : 4f(x)=(6x-1)/3 => f(x)=(6x-1)/12

CQFD.

nmo a écrit:

Soit f une fonction définie de IR vers IR, tel que 5f(-x)+f(1-x)=2x.
Exprimez f(x) en fonction de x.
Bonne chance.

Réponse fausse.
Je la referai plus tard.
Au plaisir !

Oui je vois bien, une faute d'innatention.
Bonne remarque, je vais réctifier.

mizmaz a écrit:

nmo a écrit:

Soit f une fonction définie de IR vers IR, tel que 5f(-x)+f(1-x)=2x.
Exprimez f(x) en fonction de x.
Bonne chance.

Réponse fausse.
Je la referai plus tard.
Au plaisir !

Supposons qu'il existe une fonction f solution à l'équation fonctionnelle de la forme suivante :

Nous aurons donc, d'après l'énoncé de départ :

Pour trouver les valeurs de a et b, il suffit donc de résoudre le système suivant :

Et donc finalement, la fonction f définie par est bien une solution à l'équation fonctionnelle. Par contre, si c'est la seule et unique, je n'en ai aucune idée.
Au plaisir !

Il n'y a aucune information sur le type de la fonction.
Ainsi, elle peut être de la deuxième degré.
P.S: c'est l'exercice 37 du livre.

nmo a écrit:

Il n'y a aucune information sur le type de la fonction.
Ainsi, elle peut être de la deuxième degré.
P.S: c'est l'exercice 37 du livre.

Aucune fonction polynôme de degrés strictement supérieur à 1 ne satisfait l'énoncé. Chose facilement déductible de par l'expression générale de la fonction polynôme.
Au plaisir !