| | Le marathon des inégalités: |  |
|
+64abdelbaki.attioui Geo konica Maths_BT amigo-6 sundial younesmath2012 Oty killua 001 alidos Soukaina Amaadour Misterayyoub xyzakaria manazerty az360 geom ali-mes kaj mima Otto_Ludwig steve 94 mr.mertasayeker mtb Nayssi expert_run Ahmed Taha (bis) Mehdi.A Laviecourante Moulay INTAHA Mit3ach W.Elluizi jacks louis powerofzeta Mehdi.O achraf_djy yasserito Le criminelle Bensouda mizmaz {}{}=l'infini houssam16 Vz Mr.Wajih itachi master marouan777 darkpseudo Sporovitch M.AlMokhtar MohE nmo soukki Othman24 . kholoud-tetouanie kira Sylphaen majdouline Abdek_M M.Marjani imanos Dijkschneier King tarask oussama1305 68 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 18:21 Lun 25 Juin 2012, 18:21 | |
| - Oty a écrit:
- a,b,c >=0 tel que deux d'entre eux ne sont jamais nul Montrer que :
 Si l'une des variables est nulle (par exemple c), l'inégalité se réduit à: 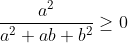 , ce qui est juste. Supposons que toutes les variables sont strictement positives, ainsi, l'inégalité est équivalente à: ^2}+\frac{1}{1+\frac{c}{b}+\left%20(%20\frac{c}{b}%20\right%20)^2}+\frac{1}{1+\frac{a}{c}+\left%20(%20\frac{a}{c}%20\right%20)^2}\geq%201) 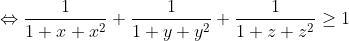 tel que: 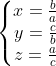 , donc: xyz=1. Il suffit montrer que: \left%20(%201+y+y^2%20\right%20)\geq%20\prod%20(1+x+x^2)) . On a: (1+y+y^2)=1+x+y+x^2+y^2+xy+xy(x+y)+x^2y^2) . Donc: (1+y+y^2)) +\sum%20x^2y^2) . Et on trouve après développement que: =x^2y^2z^2+xyz+1+\sum%20x^2+\sum%20x+\sum%20xy+\sum%20x^2y^2+xyz%20\sum%20x%20+xyz\sum%20xy+\sum%20xy(x+y)) ) (en tenant compte que xyz=1). D'où: ^2\geq%200) ... le résultat en découle. Problème: (*) Trouver la valeur maximale du réel k tel qu'on a pour tous nombres strictement positifs a,b et c l'inégalité suivante: \left%20(%20\frac{1}{a}+\frac{1}{b}+\frac{1}{c}%20\right%20)\geq%20k.\frac{a^2+b^2+c^2}{ab+ac+bc}+9-k) | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 18:27 Lun 25 Juin 2012, 18:27 | |
| ali-mes , On voit pas ton problème -_- | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 18:57 Lun 25 Juin 2012, 18:57 | |
| wa bou7dek akhay ali 7na rah tanchoofoh  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 19:44 Lun 25 Juin 2012, 19:44 | |
| | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 20:13 Lun 25 Juin 2012, 20:13 | |
| - ali-mes a écrit:
Problème: (*)
Trouver la valeur maximale du réel k tel qu'on a pour tous nombres strictement positifs a,b et c l'inégalité suivante:
\left%20(%20\frac{1}{a}+\frac{1}{b}+\frac{1}{c}%20\right%20)\geq%20k.\frac{a^2+b^2+c^2}{ab+ac+bc}+9-k) ma solution : je trouve finalement kmax=4 , pour a=b=1 , l'inégalité est equivalent a : =(4-k)c^3+(2k-6)c^2-ck+2&space;\geq{0}) on a : f(0)=2 >=0 d'ou pour que cette inégalité soit tjrs vrai il suffit que f'(c) > 0 (car c>0 ) on a : f'(c)=(12-3k)c²+(4k-12)c-k , le décriminant est D=4(k-6)² on remaque que pour cette equation admet deux solution c2 =< c1=-1 d'ou pour que f'(c) > 0 il suffite que 12-3k >=0 ainsi k=< 4 d"ou kmax=4 . Pour kmax=4 on pose : \sum a= 3u , \sum ab=3v² , abc=w^3 , l'inégalité est equivalent a g(w^3)=Aw^3 + B >=0 qui est linéaire en w^3 d'ou il suffit de prouver l'inégalité seulement pour a=b=1 et c >=0 , equivalent a : 2c²-4c+2=2(c-1)² >=0 ce qui est vrai  . Tres jolie probleme Ali  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 21:01 Lun 25 Juin 2012, 21:01 | |
| - Oty a écrit:
- a,b,c >=0 tel que deux d'entre eux ne sont jamais nul Montrer que :
 je croix qu'il vrai pour a,b,c des reels . je posterai ma solution ou j'ai utiliser \sum a/b+c sup a 1.5 pour a,b,c des reels positifs | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Lun 25 Juin 2012, 22:29 Lun 25 Juin 2012, 22:29 | |
| a,b,c >=0 tel que : ab+bc+ca=3 Prouver que : 
Dernière édition par Oty le Mar 26 Juin 2012, 02:34, édité 1 fois | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 01:13 Mar 26 Juin 2012, 01:13 | |
| - Oty a écrit:
- a,b,c >=0 tel que deux d'entre eux ne sont jamais nul Montrer que :
 d'apres holder on a (1+1+1)(sumcyclic{a(a²+ab+b²)})(sumcyclic{a²/(a²+ab+b²)}) >=(a+b+c)^3 donc T=sumcyclic{a²/(a²+ab+b²)}>=(a+b+c)^3/{3(sumcyclic{a(a²+ab+b²)})} non ça donne rien je me suit trompé je vais demarer autrement | |
|
  | |
younesmath2012
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Localisation : casa
Date d'inscription : 23/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 01:18 Mar 26 Juin 2012, 01:18 | |
| - Oty a écrit:
- Prouver que pour tout a,b,c appartenant a [-1,1] on a : 1+2abc >= a²+b²+c² .
je crois que c'est faux prend par exemple le triplet (1,0,1) tu aura 1>=2 qui est fausse | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 02:19 Mar 26 Juin 2012, 02:19 | |
| - younesmath2012 a écrit:
- Oty a écrit:
- Prouver que pour tout a,b,c appartenant a [-1,1] on a : 1+2abc >= a²+b²+c² .
je crois que c'est faux prend par exemple le triplet (1,0,1) tu aura 1>=2 qui est fausse oui désolé le probleme est erroné je vais le changé | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 09:57 Mar 26 Juin 2012, 09:57 | |
| - Oty a écrit:
- a,b,c >=0 tel que : ab+bc+ca=3 Prouver que :
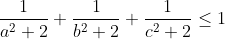 Bon je propose Ma solution   f est concave , d'après Jensen :  Donc il suffit de montrer que :  et comme f est décroissante, il faut montrer que :  ( ce qui est vrai ) | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 10:46 Mar 26 Juin 2012, 10:46 | |
| Problème ** :soit (a,b,c) > 0 tels que abc=1 Montrez que :  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 12:05 Mar 26 Juin 2012, 12:05 | |
| | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 12:27 Mar 26 Juin 2012, 12:27 | |
| | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 | |
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 13:30 Mar 26 Juin 2012, 13:30 | |
| Problème :Prouver que pour tous réels strictement positifs x,y,z :  | |
|
  | |
alidos
Expert grade2

 Nombre de messages : 352 Nombre de messages : 352
Age : 28
Localisation : Goulmima
Date d'inscription : 04/02/2012
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 13:57 Mar 26 Juin 2012, 13:57 | |
| - Oty a écrit:
- a,b,c >=0 tel que : ab+bc+ca=3 Prouver que :
 Salut, voici ce que j'ai fait: On a: (b^2+2)}{(a^2+2)(b^2+2)(c^2+2)}) }{(a^2b^2+2a^2+2b^2+4)(c^2+2)}) 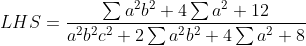 Donc, on doit montrer que: 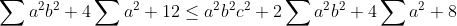 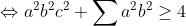 . On pose: 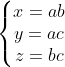 , il vient que: x+y+z=3. Et l'inégalité à démontrer est: 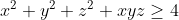 . d'après l'inégalité de Schur: ^3+9xyz\geq%204(x+y+z)(xy+xz+yz)) donc: ) d'où: 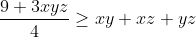 Et d'après l'IAG: ^{\frac{1}{3}}\Rightarrow%20xyz\leq%201\Rightarrow%20\frac{5+xyz}{2}\geq%20\frac{9+3xyz}{4}) . Donc: 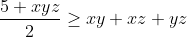 +xyz\geq4) ^2-2(xy+xz+yz)+xyz\geq4) 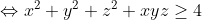 . Le résultat en découle ... | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 15:27 Mar 26 Juin 2012, 15:27 | |
| - abdelkrim-amine a écrit:
- Problème :
Prouver que pour tous réels strictement positifs x,y,z :
 ma solution pour cette inégalite : l'inégalité est homogène alors on assume : x+y+z=1 , Posant ^2}) , par shur on a quelque soit a,b,c >=0 on a : a²+b²+c²+ (9abc)\(a+b+c) >= 2(ab+ac+bc) , On prend : a= 1\(x+y) , b=1\(y+z) .... on obtient :  ou p=xy+yz+xz et r=xyz . ainsi =K) d'ou il suffit de prouver que K >=9\4 , or ceci est equivalent a : 9r(5p+1)-27p²+7p >=0 , par shur avec x+y+z=1 , on a 9r >= 4p-1 d'ou il suffit de prouver que : (5p+1)-27p^2+7p\geq{0}) equivalent a : 2 - (7p-3)² >=0 . ce qui est vrai car p=< 1\3 par AM-GM ... | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 18:13 Mar 26 Juin 2012, 18:13 | |
| Ok pose une autre inégalité  | |
|
  | |
Maths_BT
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 28
Localisation : Meknès
Date d'inscription : 08/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mar 26 Juin 2012, 20:29 Mar 26 Juin 2012, 20:29 | |
| Amigo ouvre ton cul pour que je te la passes  | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 27 Juin 2012, 17:32 Mer 27 Juin 2012, 17:32 | |
| soient a,b et c des reels positives tq: a+b+c=3 . M.Q:
ab/(b^3+1) +ac/(a^3+1) + bc/(c^3+1) inf=2 | |
|
  | |
Maths_BT
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 28
Localisation : Meknès
Date d'inscription : 08/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 27 Juin 2012, 18:57 Mer 27 Juin 2012, 18:57 | |
| pour l'inégalité de killua  / avec Iag On pose S =ab/(b^3+1) +ac/(a^3+1) + bc/(c^3+1) on a : ab / b^3 +1/2+1/2 =< a/3 rac cub (1/4) En sommant ça donne : S =< 1/ (3*rac cub (1/4) ) (a+b+c) <==> S =< 1/ rac cub (1/4) =< rac cub (4) et comme on a : rac cub (4) =< 2 ça donne S =< 2 | |
|
  | |
killua 001
Maître

 Nombre de messages : 145 Nombre de messages : 145
Age : 29
Localisation : Ma chambre :D
Date d'inscription : 02/05/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 27 Juin 2012, 19:19 Mer 27 Juin 2012, 19:19 | |
| jolie .... poste une autre !!! | |
|
  | |
Maths_BT
Habitué
 Nombre de messages : 19 Nombre de messages : 19
Age : 28
Localisation : Meknès
Date d'inscription : 08/06/2012
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  Mer 27 Juin 2012, 19:37 Mer 27 Juin 2012, 19:37 | |
| avec plaisir  { a,b,c} >0 avec Rac ( (a²+b²+c²) / 3 ) = 1 M.Q : 1/a(a+1) + 1/b(b+1) + 1/c(c+1) >= 1/2 | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Le marathon des inégalités: Sujet: Re: Le marathon des inégalités:  | |
| |
|
  | |
| | Le marathon des inégalités: |  |
|
