Préparations aux olympiades de première (2010-2011)

Dans ABC, on a l'angle A et AC, donc on peut avoir le rapport sin(B)/BC, et puisqu'on a MB, alors on peut faire dépendre linéairement sin(B) et MC.
Dans ABM, on a AM et l'angle BAM, donc on peut faire dépendre linéairement sin(B) et AM.
Or MC²=AC²+AM²=1+AM², donc on peut obtenir sin(B) en utilisant les dépendances linéaires et cette dernière équation.
On en déduit tout ce qu'on veut.

nmo a écrit:

darkpseudo a écrit:

Tu devrait lire j'ai déjà dis pour p=2 on 3^2 = 9 qui n'est pas premier . Bon cet exo mérite vraiment pas un autre post , oublions le vite te passons à autre chose

Ce que je veux dire est pourquoi: ?
Et cela necessite d'être prouvé.

3^p (croissance exponentielle) croît beaucoup plus rapidement que (p-2)² (croissance polynomiale), donc il suffit de tester pour les petits cas.

Déjà pour celui d'avant on a f(x)=e^(xln3)-(x-2)^2 est strictement croissante et donc f(x)>f(3)>2 .
Pour celui que tu viens de proposer c'est un classique . ( je m'excuse pour l'exo d'avant )

Dijkschneier a écrit:

Le problème précédent n'est qu'un problème calculatoire (définir un repère, avoir les coordonnées de l'orthocentre, and you're done !), et j'attends par conséquent le problème 84.

Peux tu donner une petite explication ?
ou un lien ou je peux trouver l'explication exacte

Amicalement

Merci d'avance

Dijkschneier a écrit:

Dans ABC, on a l'angle A et AC, donc on peut avoir le rapport sin(B)/BC, et puisqu'on a MB, alors on peut faire dépendre linéairement sin(B) et MC.
Dans ABM, on a AM et l'angle BAM, donc on peut faire dépendre linéairement sin(B) et AM.
Or MC²=AC²+AM²=1+AM², donc on peut obtenir sin(B) en utilisant les dépendances linéaires et cette dernière équation.
On en déduit tout ce qu'on veut.

nmo a écrit:

darkpseudo a écrit:

Tu devrait lire j'ai déjà dis pour p=2 on 3^2 = 9 qui n'est pas premier . Bon cet exo mérite vraiment pas un autre post , oublions le vite te passons à autre chose

Ce que je veux dire est pourquoi: ?
Et cela necessite d'être prouvé.

3^p (croissance exponentielle) croît beaucoup plus rapidement que (p-2)² (croissance polynomiale), donc il suffit de tester pour les petits cas.

Pour le dernier exo , on peut aussi faire dépendre CD et AB après quelques calcul on obtien CD*AB = 2 ( si je ne m'abuse ) ; et ensuite après d'autre calcul
CD=2^(1/3)

darkpseudo a écrit:

Pour le dernier exo , on peut aussi faire dépendre CD et AB après quelques calcul on obtien CD*AB = 2 ( si je ne m'abuse ) ; et ensuite après d'autre calcul
CD=2^(1/3)

C'est la bonne réponse.
Tu peux proposer un exercice si tu veux.

Ok merci :
Problème 84:
Assez facile , soit x et y deux entiers tel que xy|(x^2+y^2-x)
Prouvez que x est un carré parfait .

darkpseudo a écrit:

Ok merci :
Problème 84:
Assez facile , soit x et y deux entiers tel que xy|(x^2+y^2-x)
Prouvez que x est un carré parfait .

C'est le problème 85.
Merci de rectifier.

d=pgcd(x,y), x=dx', y=dy'
d² | d²x'y' = xy | x²+y²-x = d²x'² + d²y'² - dx' ===> d² | dx' ===> d|x' ===> x'=dx'' ===> x=d²x''²
x | xy | x²+y²-x ===> x | y² ===> d²x'' | d²y'² ===> x'' | y'²
x'' et y'² premiers entre eux ===> x''=1
Done !

nmo a écrit:

En attendant une réponse, je propose un autre exercice:
Exercice 84:
Soit ABC un triangle tel que AC=1.
Soit M un point qui appartient à [BC] tel que et et MB=1.
Calculez CM et AB.
Bonne chance.

est ce que vous avez trouve CM= et AB=?

merci d'avance

Oui oui c'est bien ça .

Dijkschneier a écrit:

d=pgcd(x,y), x=dx', y=dy'
d² | d²x'y' = xy | x²+y²-x = d²x'² + d²y'² - dx' ===> d² | dx' ===> d|x' ===> x'=dx'' ===> x=d²x''²
x | xy | x²+y²-x ===> x | y² ===> d²x'' | d²y'² ===> x'' | y'²
x'' et y'² premiers entre eux ===> x''=1
Done !

Pour quelle raison les deux naturelles x" et y'² sont premiers entre eux ?

M.Marjani a écrit:

Pour quelle raison les deux naturelles x" et y'² sont premiers entre eux ?

Superbe question, pour ma part, j'ai seulement trouvé que: PGCD(x,y²)=PGCD(d²x'',d²y²)=d².PGCD(x",y²).
Ainsi pour que x'' et y'² soient premiers entre eux, il faut que PGCD(x,y²)=d².
Je me suis bloqué ici, on attend donc l'intervention de Dijkschneier.
En attente d'une solution complète, je propose le dernier exercice de mon interrogation écrite:
Exercice 86:
Soient 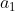, 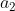, ..., 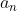, 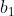, 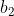, ..., et 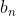des réels.
Démontrez qu'on a: .
Bonne chance.

Solution du 86éme problème:
En posant
On obtient alors de l'inégalité triangulaire que:
D'ou découle le résultat voulu.

W.Elluizi a écrit:

On obtient alors de l'inégalité triangulaire que:

Il faut le démontrer.

nmo a écrit:

W.Elluizi a écrit:

On obtient alors de l'inégalité triangulaire que:

Il faut le démontrer.

Pour ce faire,rien de plus simple qu'une récurrence sur n:
Admettons en un premier temps que:

donc:
Et on posant encore:
On ré-applique l'inégalité triangulaire:
Et le résultat en découle.

W.Elluizi a écrit:

nmo a écrit:

W.Elluizi a écrit:

On obtient alors de l'inégalité triangulaire que:

Il faut le démontrer.

Pour ce faire,rien de plus simple qu'une récurrence sur n:
Admettons en un premier temps que:

donc:
Et on posant encore:
On ré-applique l'inégalité triangulaire:
Et le résultat en découle.

Bien. Tu peux poster ton problème.

Je ne dispose actuellement d'aucun problème comportant de l'intérêt,donc que chacun se sente libre d'en poster un.

Je propose:
Exercice 87:
Trouvez le plus petit entier n tel que et n est compris entre 1000 et 1111.
Bonne chance.

Je parie qu'il s'agit là aussi d'un problème marocain

M.Marjani a écrit:

Dijkschneier a écrit:

d=pgcd(x,y), x=dx', y=dy'
d² | d²x'y' = xy | x²+y²-x = d²x'² + d²y'² - dx' ===> d² | dx' ===> d|x' ===> x'=dx'' ===> x=d²x''²
x | xy | x²+y²-x ===> x | y² ===> d²x'' | d²y'² ===> x'' | y'²
x'' et y'² premiers entre eux ===> x''=1
Done !

Pour quelle raison les deux naturelles x" et y'² sont premiers entre eux ?

Je crois avoir trouvé une réponse à cette question:
On pose: k=PGCD(x,y²), on a d'un côté: k=PGCD(x,y²)=PGCD(d².x'',d².y'²)=d².PGCD(x'',y'²).
Et d'un autre côté:
.
Donc x'' et y'² sont premiers entre eux.
Sauf erreur.

Pourquoi tant de peine nmo ?
Puisque x' et y' sont premiers entre eux, alors x' et y' ne partagent aucun facteur en commun, et donc leurs diviseurs à fortiori n'en partagent pas non plus !!
La morale, c'est de toujours utiliser la décomposition en facteurs premiers pour vérifier mentalement la primalité entre deux entiers...
Tout comme le ferait un algorithme simpliste...

Dijkschneier a écrit:

Je parie qu'il s'agit là aussi d'un problème marocain

Je ne suis pas au courant de sa source, mais il est ennuyeux.
Je sais la procédure de résolution, que je vais écrire après deux jours si personne ne me devance.
Et voici un problème de plus:
Problème 88:
Soit a et b deux entiers naturels tel que 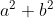soit premier.
Démontrez que l'équattion n'admet pas de solutions entières.
Bonne chance.

a^2-4b-4 = p - b^2-4b-4 = p-(b+2)^2
Il faut que ce nombre soit un carré parfait CAD p = x^2+(b+2)^2 or on a déjà
p= a^2+b^2 et on sait d'après le théorème des deux carré qu'un nombre premier p =1[4] s'écris de façon unique sous la forme de deux carré
donc a = b+2 et x=b donc p = b^2+(b+2)^2 = b^2+b^2+4b+4 qui est pair et ceci est une contradiction avec le fait que p soit premier et p ne peut être égal à 2 car 2b^2+4b+4 > 2 .

Joli.