| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
+46Norax Mehdi-el redouaneamraouza Misterayyoub diablo902 *youness* Loliiiita kaj mima ilyasaitazzi l'intellectuelle az360 konica darkpseudo Mehdi.O maths_lady mathadores amigo-6 K-maths youpi alumenne.b achraf_djy boubou math yumi M.Marjani Nayssi Meded louis yasserito master Othmaann houssa ayoubmath nmo Dijkschneier mizmaz belkhayaty Azerty1995 tarask Hamouda anas-az_137 matheux-xman Ahmed Taha (bis) maths-au-feminin A446 supista ali-mes 50 participants |
|
| Auteur | Message |
|---|
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 25 Mar 2012, 20:10 Dim 25 Mar 2012, 20:10 | |
| on a l'inégalité est équivalente a : ab+ac+bc-2abc >1\4 , maintenant on pose : a=x+y , b=y+z , c=x+z ; on a x+y+z=1\2 , l'inégalité se transforme en : x²+y²+z²+2(xy+yz+xz)+2xyz > 1\4 , équivalant a : (x+y+z)²+2xyz >1\4 équivalent : xyz >0 ce qui est vrai . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 27 Mar 2012, 13:13 Mar 27 Mar 2012, 13:13 | |
| Problème 95 : a,b,c >=0 . Prouver que : }+\frac{1}{c(b+c)}+\frac{1}{a(c+a)}\geq{\frac{27}{2(a+b+c)^2}}) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 27 Mar 2012, 13:26 Mar 27 Mar 2012, 13:26 | |
| - Oty a écrit:
- Problème 95 : a,b,c >=0 . Prouver que :
}+\frac{1}{c(b+c)}+\frac{1}{a(c+a)}\geq{\frac{27}{2(a+b+c)^2}}) Solution au problème 95:d'après Holder [img]http://latex.codecogs.com/gif.latex?[\frac{1}{b(a+b)}+\frac{1}{c(b+c)}+\frac{1}{a(c+a)}](a+b+c)[(a+b)+(b+c)+(c+a)]&space;\ge&space;(1+1+1)^3 [/img] d'où le résultat 
Dernière édition par diablo902 le Mar 27 Mar 2012, 22:35, édité 1 fois | |
|
  | |
Soukaina Amaadour
Maître

 Nombre de messages : 230 Nombre de messages : 230
Age : 27
Localisation : Casablanca, Maroc
Date d'inscription : 13/10/2011
 | |
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 27 Mar 2012, 19:43 Mar 27 Mar 2012, 19:43 | |
| Bonsoir , je ne vois pas ou est l'inégalité de Holder dans ton expression tu peux préciser ? | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mar 27 Mar 2012, 20:09 Mar 27 Mar 2012, 20:09 | |
| Pour le problème 96: on prend x=0 on a : |c| =< 1 , pour la 2) on prend x=1 puis x=-1 en sommant on obtient le résultat , 3) toujours avec x=1 et x=-1 en faisant la différence des deux inégalité on trouve |b|=<1 , et on a a²+b²+c²=(|a+b+c|)²-2b(a+c)-2bc =<1+2(|b|.|a+c|+|bc|) =<1+2(1+1)=5 ( car |x| >= x quelque soit x dans R) | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Mer 28 Mar 2012, 00:00 Mer 28 Mar 2012, 00:00 | |
| Problème 97 : x,y>=0 tel que : 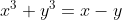 . Montrer que :  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 13:47 Jeu 29 Mar 2012, 13:47 | |
| - Oty a écrit:
- Problème 97 : x,y>=0 tel que :
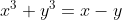 . Montrer que : . Montrer que :  . . Je pense que quelque chose ne marche pas bien dans cet exercice. En effet, si on considère x un paramètre, l'équation 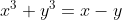 , dont l'inconnue est y, admet une solution réelle ^2+108}+27x)^{\frac{1}{3}}}{3.2^{\frac{1}{3}}}+\frac{2^{\frac{1}{3}}}{(-27x^3+\sqrt{(27x-27x^3)^2+108}+27x)^{\frac{1}{3}}}) . (Tu peux utiliser la méthode de Cardan ou voir dans le lien suivant: [url]http://www.wolframalpha.com/input/?i=x-x^3%3Dy%2By^3 [/url]). Et ainsi, l'inégalité à démontrer s'écrit ^2+108}+27x)^{\frac{1}{3}}}{3.2^{\frac{1}{3}}}+\frac{2^{\frac{1}{3}}}{(-27x^3+\sqrt{(27x-27x^3)^2+108}+27x)^{\frac{1}{3}}})^2<1) . Ce qui n'est pas valide, d'après Wolfram Alpha: [url]http://www.wolframalpha.com/input/?i=4%28\frac{%28-27x^3%2B\sqrt{%2827x-27x^3%29^2%2B108}%2B27x%29^{\frac{1}{3}}}{3.2^{\frac{1}{3}}}%2B\frac{2^{\frac{1}{3}}}{%28-27x^3%2B\sqrt{%2827x-27x^3%29^2%2B108}%2B27x%29^{\frac{1}{3}}}%29^2%2Bx^2%3C1 [/url]. Veille à vérifier l'énoncé. | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 18:56 Jeu 29 Mar 2012, 18:56 | |
| je ne vois pas vraiment pourquoi tout c'est calcule ? il n'y a pas d'erreur dans l'énoncé et l'inégalité ce démontre simplement , pas besoin de cardan . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 19:02 Jeu 29 Mar 2012, 19:02 | |
| si x=y , d’après la condition x=0 l'inégalité est vérifier . si x différent de y , il suffit de remarque que (x-y)(x²+4y²) < x^3+y^3 , car ceci est équivalent a : 4y²x-yx² - 5y^3=-y(y²+(2y-x)²) < 0 d'ou le résultat d’après la condition . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 20:05 Jeu 29 Mar 2012, 20:05 | |
| Problème 98 : a,b,c > 0 tel que : abc=1 . Prouver que : (b+1)}+\frac{b}{(b+1)(c+1)}+\frac{c}{(c+1)(a+1)}\geq{\frac{3}{4}}) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 20:18 Jeu 29 Mar 2012, 20:18 | |
| - Oty a écrit:
- Problème 98 : a,b,c > 0 tel que : abc=1 . Prouver que :
(b+1)}+\frac{b}{(b+1)(c+1)}+\frac{c}{(c+1)(a+1)}\geq{\frac{3}{4}}) l'inégalité est équivalente à }{\prod%20(c+1)}%20\ge%20\frac{3}{4}) ou bien  une application directe d'IAG  | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 21:12 Jeu 29 Mar 2012, 21:12 | |
| oui bravo  . | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 21:19 Jeu 29 Mar 2012, 21:19 | |
| Problème 99:Salut, 
Dernière édition par diablo902 le Jeu 29 Mar 2012, 23:18, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 22:17 Jeu 29 Mar 2012, 22:17 | |
| - Oty a écrit:
- si x=y , d’après la condition x=0 l'inégalité est vérifier . si x différent de y , il suffit de remarque que (x-y)(x²+4y²) < x^3+y^3 , car ceci est équivalent a : 4y²x-yx² - 5y^3=-y(y²+(2y-x)²) < 0 d'ou le résultat d’après la condition .
Sans mentir, je n'ai jamais vu une telle solution. Bravo. Cependant, ta solution manque de précision: Tu dois démontrer que x est supérieur ou égal à y, ce qui est trivial depuis l'hypothèse. Ensuite, l'inégalité à prouver doit être large: En effet, le couple (1,0) mène vers une égalité. Au plaisir! | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 23:35 Jeu 29 Mar 2012, 23:35 | |
| on pose : a=max(a,b,c) , l'inégalité est équivalente a : a(b-c)²(b+c-a)+b(a-b)(a-c)(a+b-c) >=0 ce qui vrai d’après l'inégalité triangulaire . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Jeu 29 Mar 2012, 23:52 Jeu 29 Mar 2012, 23:52 | |
| Problème 100 7adide jami3e azwaje (a,b) min z² bi7ayte : 2ab=a+b+4 . | |
|
  | |
Oty
Expert sup
 Nombre de messages : 745 Nombre de messages : 745
Localisation : casablanca
Date d'inscription : 02/03/2012
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Ven 30 Mar 2012, 00:24 Ven 30 Mar 2012, 00:24 | |
| Merci nmo  . | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 12:12 Dim 15 Avr 2012, 12:12 | |
| - Oty a écrit:
- Problème 100 7adide jami3e azwaje (a,b) min z² bi7ayte : 2ab=a+b+4 .
Je propose une solution, même si l'exercice est facile: L'équation proposée équivaut à (2a-1)(2b-1)=4ab-2a-2b+1=2(2ab-a-b)+1=2*4+1=9. Comme les diviseurs de 9 sont -1, -3, -9, 1, 3, 9 on doit étudier un tas de cas. On peut réduire ces cas en remarquant la symétrie du problème: _Si 2a-1=-1 et 2b-1=-9, alors a=0 et b=-4. _Si 2a-1=-3 et 2b-1=-3, alors a=-1 et b=-1. _Si 2a-1=1 et 2b-1=9, alors a=1 et b=5. _Si 2a-1=3 et 2b-1=3, alors a=2 et b=2. Il s'ensuit que les couples solutions sont (0,4); (4,0); (1,5); (5,1); (-1,-1) et (2,2). Sauf erreurs. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 12:23 Dim 15 Avr 2012, 12:23 | |
| probleme 101 :ABCD inscriptible et les deux bissectrice de DBC et DAC se coupet en L . montrer que : L appartenant au cercle circonscrit du triangle ABC .  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 15:52 Dim 15 Avr 2012, 15:52 | |
| Solution au Problème 101: - Spoiler:
Lemme: Soit ABC un triangle, et I le centre de son cercle inscrit, D la deuxième intersection de la bissectrice intérieure de l'angle 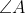 avec le cercle circonscrit au triangle ABC, est le centre du cercle circonscrit au triangle BIC. Preuve:  On a: 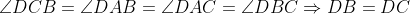 Et on a: 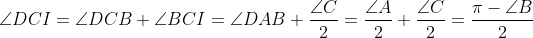 Et: 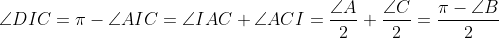 Donc: 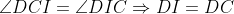 . Il s'en suit que D est le centre du cercle circonscrit au triangle BIC. Revenons au problème initial:  Soit I_a le centre du cercle inscrit au triangle BCD, et L_a la deuxième intersection de la bissectrice intérieure de angle{DBC} avec le cercle circonscrit au quadrilatère ABCD. On définit de la même manière les points I_b et L_b. D'après le lemme, L_a est le centre du cercle circonscrit au triangle CDI_a, donc L_a appartient au médiatrice du segment [CD] et l'arc (CD) du cercle (ABCD) ne contenant pas B. De même, on trouve que L_b est le centre du cercle circonscrit au triangle CDI_b, donc L_b appartient au médiatrice du segment [CD] et l'arc (CD) du cercle (ABCD) ne contenant pas A. Donc: L_a=L_b , et le résultat en découle...
Problème 102: Soient a,b et c des réels positifs. Montrer que: ^2%20+%20b(b-c)^2%20\geq%20(a%20-%20c)(b%20-%20c)(a+b-c)) | |
|
  | |
diablo902
Maître
 Nombre de messages : 279 Nombre de messages : 279
Age : 27
Date d'inscription : 01/07/2011
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 16:38 Dim 15 Avr 2012, 16:38 | |
| @ Ali: ce lemme" Soit ABC un triangle, la deuxième intersection de la bissectrice intérieure de l'angle A avec le cercle circonscrit au triangle ABC est le milieu de l'arc BC" est suffisant pour conclure dans quelques lignes  ! Solution au problème 102:l'inégalité est équivalente à ) ce qui est une application directe de Schur! (n=1) Je n'ai pas de problème à proposer | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 17:25 Dim 15 Avr 2012, 17:25 | |
| - diablo902 a écrit:
- @ Ali: ce lemme"Soit ABC un triangle, la deuxième intersection de la bissectrice intérieure de l'angle A avec le cercle circonscrit au triangle ABC est le milieu de l'arc BC" est suffisant pour conclure dans quelques lignes
 ! !
Hein !? Je ne vois pas l'utilité de ce commentaire, puisque c'est presque la même chose que j'ai fait !
Dernière édition par ali-mes le Dim 15 Avr 2012, 22:24, édité 1 fois | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  Dim 15 Avr 2012, 18:12 Dim 15 Avr 2012, 18:12 | |
| ma solution de my own (mybie) probleme 101
notant : L et l'intersection du deux bissectrices
on a : DBC = DAC alors LBC = LAC et ca implique que : LCBA est inscriptibles d'ou le resultat !! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011) Sujet: Re: Préparations aux olympiades de tronc commun (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2010-2011) |  |
|
