| | Préparation à la première SM (La logique) |  |
|
+13Nayssi darkpseudo upsilon az360 expert_run boubou math salimreda sanfoura9 yasserito Ahmed Taha (bis) geom ali-mes Azerty1995 17 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 01:21 Dim 07 Aoû 2011, 01:21 | |
| Pour le 1): cela ne me convient pas, il faut utiliser une simple récurrence sur n. f(x+n+1)=f(x+n)+1=f(x)+n+1. 2) + 3) => je crois que c'est juste ! 4) Je crois qu'on ne peut pas conclure les fonctions qui satisfont la condition à partir de la subtitution de x par 1/n. Pourquoi? => t'as prouvé que c'est la fonction identique pour tout rationnel qui s'écrit sous la forme 1/n, et pour 2/3 et 7/8 et les autres rationnels qui ne s'écrivent pas sous la forme 1/n ? Je crois qu'il faut faire la substitution de x par a/b (la définition des nombres rationnels) avec (a,b)£IN x IN* puis remplacer n par b (au moins, c'est ce que j'ai fait  ) et tu auras f(a/b)=a/b (Maintenant tu peux conclure qu'il s'agit de l'identique sur Q+*, car tout rationnel strictement positif peut s'écrire sous la forme a/b) J'espère que ce que j'ai dit n'est pas de pur charabia  !! En tous cas, propose un autre exo !
Dernière édition par ali-mes le Dim 07 Aoû 2011, 01:48, édité 1 fois | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 01:39 Dim 07 Aoû 2011, 01:39 | |
| Merci pour l'explication.ali-mes. Cependant, je n'ai pas bien compris ta methode pour la première question: f(x+n+1)= f(x+n)+1 =f(x)+n+1 ? J'espère que tu me l'explique plus. Amicalement  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 01:47 Dim 07 Aoû 2011, 01:47 | |
| Pa récurrence sur n, on va montrer que: \right&space;)(\forall&space;n\;\in&space;\mathbb{N}\ast&space;):&space;\;&space;\;&space;f(x+n)=f(x)+n) Initialisation: Initialisation: Pour n=1, on a: f(x+1)=f(x)+1. Ce qui est vrai d'après les données de l'exercice. Hérédité:On suppose que: f(x+n)=f(x)+n et on montre que f(x+(n+1))=f(x)+(n+1) On a f(x+(n+1))=f(x+n+1)=f((x+n)+1)=f(x+n)+1 (d'après les données) Donc: f(x+(n+1))=f(x+n)+1=f(x)+n+1 (D'après l'hypothèse de la récurrence) Synthèse de la récurrence: \right&space;)(\forall&space;n\;\in&space;\mathbb{N}\ast&space;):&space;\;&space;\;&space;f(x+n)=f(x)+n) J'espère que c'est clair, maintenant tu peux proposer ton exercice ! | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 02:09 Dim 07 Aoû 2011, 02:09 | |
| Merci... Et voici l' Exercice 20 | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 20:52 Dim 07 Aoû 2011, 20:52 | |
| Solution de l'exercice 20- Spoiler:
Suposons que cette fonction existe Prenos y=0 on aura ^{f(0)}=0) Donc f(x)=0 d'ou }=0) d'ou \neq 0) or on a f(x)=0 pour tout x de N d'ou la contradiction donc il n'existe pas une tell fonction.
| |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 20:55 Dim 07 Aoû 2011, 20:55 | |
| Exercice 21Montrez qu'il n'existe pas entier naturel n tel que 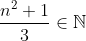 | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 22:00 Dim 07 Aoû 2011, 22:00 | |
| Quelque soit n de Z, n² est congru 0 ou 1 modulo 3 ainsi n²+1 est congru 1 ou 2 modulo 3 , ce qui finit la démonstration. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 14:47 Mer 10 Aoû 2011, 14:47 | |
| Exercice 22Soit x et y deux nombres positifs posant : x+y=s Montrez que ) | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 15:26 Mer 10 Aoû 2011, 15:26 | |
| - Azerty1995 a écrit:
- Exercice 22
Soit x et y deux nombres positifs posant : x+y=s
Montrez que ) c'est facile on utilisons Jenson | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 | |
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 15:44 Mer 10 Aoû 2011, 15:44 | |
| voici ma reponse - Spoiler:
race(4x+1)+race(4y+1)<=2(s+1)
race(4x+1)+race(4y+1)<=2(x+y+1)
2race(4x+1)+2race(4y+1)<=4(x+y+1)
4(x+y+1)-2race(4x+1)-2race(4y+1)>=0
4x+4y+4-2race(4x+1)-2race(4y+1)>=0
4x-2race(4x+1)+2+4y-2race(4y+1)+2>=0
(race(4x+1)+1)²+(race(4y+1))²>=0
et ca ets vrais alors race(4x+1)+race(4y+1)>=2(s+1)
 | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 15:48 Mer 10 Aoû 2011, 15:48 | |
| et ca est  vrais alors race(4x+1)+race(4y+1)<=2(s+1) | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 15:57 Mer 10 Aoû 2011, 15:57 | |
| proposes un autre Salimreda ! | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 16:03 Mer 10 Aoû 2011, 16:03 | |
| ok mais attendezun peut slv je vais chercher un exo  | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 16:47 Mer 10 Aoû 2011, 16:47 | |
| voici mon exo soient (x,y,z) trois reels positifs démontrez que si x²-y est déférent de z² alors race(x+race(y))est déférent de race((x+z)/2)+race((x-z)/2) allez bonne chance  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 21:28 Mer 10 Aoû 2011, 21:28 | |
| Solution de l'exercice 23- Spoiler:
| |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 21:45 Mer 10 Aoû 2011, 21:45 | |
| bravo Azerty1995 c'est la bonne reponse alors proposez un exo slv  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 22:02 Mer 10 Aoû 2011, 22:02 | |
| Ok Exercice 24Soit x, y et z trois réels Montrez que 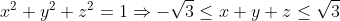 | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 22:46 Mer 10 Aoû 2011, 22:46 | |
| Solution de l' Exercice 24- Spoiler:
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 10 Aoû 2011, 22:54 Mer 10 Aoû 2011, 22:54 | |
| Azerty1995, dans votre solution tu as fait: \Leftrightarrow&space;(p\Rightarrow&space;q)) ce qui est clairement faux d'après le tableau de vérité, c'est plutôt: \Leftrightarrow&space;(q\Rightarrow&space;p)) Mais quand même, on peut suivre les étapes de ta démonstration, mais on va commancer de la fin jusqu'à le début, car en réalité, il s'agit des équivalences et pas des implications. | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 11 Aoû 2011, 00:21 Jeu 11 Aoû 2011, 00:21 | |
| Ah oui je vois que que j'ai pas encore bien saisis les lois de logique, merci pour l'info  | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 11 Aoû 2011, 16:05 Jeu 11 Aoû 2011, 16:05 | |
| Exercice 25
Montrez qu'il n'existe aucun pôlynome P(x)=ax^3+bx²+cx+d
Tel que a et b et c et d des nombres de Z et vérifient P(1)=1 et P(2007)=2
| |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 12 Aoû 2011, 21:02 Ven 12 Aoû 2011, 21:02 | |
| | |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 12 Aoû 2011, 21:16 Ven 12 Aoû 2011, 21:16 | |
| - upsilon a écrit:
- Toujours pas de réponse?
i faut montrer que x-y divise P(x)-P(y)... | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  | |
| |
|
  | |
| | Préparation à la première SM (La logique) |  |
|
