| | Préparation à la première SM (La logique) |  |
|
+13Nayssi darkpseudo upsilon az360 expert_run boubou math salimreda sanfoura9 yasserito Ahmed Taha (bis) geom ali-mes Azerty1995 17 participants |
|
| Auteur | Message |
|---|
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 28 Juil 2011, 18:43 Jeu 28 Juil 2011, 18:43 | |
| - Azerty1995 a écrit:
Je conaissais pas ça
donc ça doit etre pour tout x de R x²-7x+6=0 et x=/2 est c'est faux en prenant x=2
Donc A est vraie
Et pour B il existe un x de R x²>4 et x=<2
On a x²>=4 <=> x>2 et puisque x=<2 alors 2<x=<2 c'est impossible donc B est vraie
J 'attends ta confirmation pour éditer mon message précedant
maintenant c'est juste, à toi le prochain exo ! | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 28 Juil 2011, 18:55 Jeu 28 Juil 2011, 18:55 | |
| Un peu de reccurence Exercice 71)Montrez que ; n^{2}> 2n+1) 2)Montrez que ^{n}) est divisible par 11 pour tout n de IN* | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 28 Juil 2011, 21:48 Jeu 28 Juil 2011, 21:48 | |
| salut a tous 1- on a 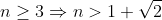 donc ^{2}%3E&space;2) et 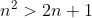 2- 2- on a (a^{n-1}+a^{n-2}b+...+ab^{n-2}+b^{n-1})) d'ou ^{n}=(10-(-1))(10^{n-1}+10^{n-2}+...+10+1)) ) donc ^{n}) est divisé par 11
Dernière édition par abdelkrim-amine le Ven 29 Juil 2011, 11:55, édité 1 fois | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 28 Juil 2011, 21:54 Jeu 28 Juil 2011, 21:54 | |
| pr la premiere pas neccessairement recurrence:
on a n>2 et n-2>=1 alors n(n-2)>2 ainsi n²>2n+2 (c mieux que +1)
alors n²>2n+1
Deuxieme pas necessairement recurrence,on peut utiliser la formule directe de a^n-b^n ,
mais si c'est hors programme recurrence est le seul choix ou bien :
10 = -1[11] alors 10^n= (-1)^n [11] ainsi 10^n-(-1)^n=0[11]
| |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 10:33 Ven 29 Juil 2011, 10:33 | |
| Je veux savoir est se que la méthode suivante vraie ou fausse pour le premier exo: on suppose que  et on a  alors  ce qui est vrai. | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 10:43 Ven 29 Juil 2011, 10:43 | |
| Je ne crois pas geom que ta methode est vraie car ce ne sont pas des equivalences, c'est pr cela que cette methode est nomme la methode des equivalences consecutives.. | |
|
  | |
geom
Maître
 Nombre de messages : 189 Nombre de messages : 189
Age : 30
Date d'inscription : 30/04/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 11:28 Ven 29 Juil 2011, 11:28 | |
| - yasserito a écrit:
- Je ne crois pas geom que ta methode est vraie car ce ne sont pas des equivalences, c'est pr cela que cette methode est nomme la methode des equivalences consecutives..
merçi  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 13:03 Ven 29 Juil 2011, 13:03 | |
| Puisque c'est abdelkrim-amine qui a répondu le premier c'est à lui de poster un nouvel exercice. | |
|
  | |
Ahmed Taha (bis)
Expert grade2
 Nombre de messages : 353 Nombre de messages : 353
Age : 29
Localisation : kénitra
Date d'inscription : 06/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 14:18 Ven 29 Juil 2011, 14:18 | |
| salut a tous Exercice 8resoudre dans 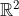 le système : 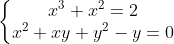 | |
|
  | |
yasserito
Expert sup
 Nombre de messages : 615 Nombre de messages : 615
Age : 29
Localisation : Maroc
Date d'inscription : 11/07/2009
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 29 Juil 2011, 15:16 Ven 29 Juil 2011, 15:16 | |
| Solution probleme 8:
Soit x et y de IR
x^3+x²=2 <=> (x-1)(x²+2x+2)=0 <=>(x-1)((x+1)²+1)=0 <=> x=1
Alors 1+y+y²-y=0 <=> 1+y²=0 (impossible)
Alors s=\o
Sauf erreur | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 | |
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 12:58 Sam 30 Juil 2011, 12:58 | |
| Premièrement, je me suis rendu compte que Yasserito est entrain de spammer ce sujet avec ses participations inutiles, on sait bien que t'es un futur élève de Terminale, donc pas la peine de essayer de nous montrer ce que tu as appris cette année. Si tu es inttéressé par tester tes conaissances de 1ere, je possède des vrais casse-tête, et je suis prêt de te les donner (et crois moi, pas des exos fastoches de logique  ). Si vous le permettez bien-sûr, j'ai une petite proposition: Pour que notre jeu soit un peu organisé, commençons par proposer des exos traitant les assertions et la démonstrations de quelques lois logiques et quelques implicatons ou équivalences, puis on passe au différents types de démonstration (récurrence, l'absurde, la disjonction des cas), et essayez de ne pas mélanger tous ! Et je crois, qu'il faut ajouter une nouvelle règle: si tu ne vas pas poster un nouveau exo, donc ne réponds pas !C'est juste parce que j'ai tellement hâte de voir ce joli jeu tomber dans l'eau à cause que les participant attendent le post des nouveaux exos  Bref, passons toutes ces futilités, je vous propose un autre exercice: Exercice 9:Soient a,b, x et y des réels strictement positifs, montrer que:  Quand vous sentez qu'on a travaillé beacoup d'exos traitant un certain thème, veuillez indiquer clairement ce que vous voulez travailler pour qu'on puisse changer le type d'exos. | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 13:38 Sam 30 Juil 2011, 13:38 | |
| je commence par montrer : x/y < (ax+by)/(bx+ay)
x/y < (ax+by)/(bx+ay)
équivalent à : bx²+ayx<axy +by²
" " : b(x²-y²)<0
" " : x²<y²
" " : lxl < lyl équiv à : x<y et cela 'est juste donc: x/y < (ax+by)/(bx+ay)*
: (ax+by)/(bx+ay) < y/x
équi.: ax²+bxy < bxy +ay²
équi : a(x²-y²) <0 équiv à : x<y et c'est juste donc : (ax+by)/(bx+ay) < y/x **
Alors: x/y<(ax+by)/(bx+ay) < y/x
| |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 13:43 Sam 30 Juil 2011, 13:43 | |
| je propose tt l'exo 5 de cette série (sauf la récurrence)
http://arabmaths.kegtux.org/arabmaths/zowar/1sm/0607/slogique1smkdedar.pdf | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 16:52 Sam 30 Juil 2011, 16:52 | |
| - ali-mes a écrit:
Si vous le permettez bien-sûr, j'ai une petite proposition:
Pour que notre jeu soit un peu organisé, commençons par proposer des exos traitant les assertions et la démonstrations de quelques lois logiques et quelques implicatons ou équivalences, puis on passe au différents types de démonstration (récurrence, l'absurde, la disjonction des cas), et essayez de ne pas mélanger tous !
Et je crois, qu'il faut ajouter une nouvelle règle: si tu ne vas pas poster un nouveau exo, donc ne réponds pas !
C'est juste parce que j'ai tellement hâte de voir ce joli jeu tomber dans l'eau à cause que les participant attendent le post des nouveaux exos 
Je suis d'accord pour l'organisation, mais je crois que les assertions traitées sont suffisantes pas toi? Si tout le monde est d'accord ,passons aux équivalences, implications et lois de logique PS: Je ne saisis pas ce que tu veux dire par la nouvelle régle | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 16:58 Sam 30 Juil 2011, 16:58 | |
| - sanfoura9 a écrit:
- je propose tt l'exo 5 de cette série (sauf la récurrence)
http://arabmaths.kegtux.org/arabmaths/zowar/1sm/0607/slogique1smkdedar.pdf Je pense qu'il fait mieux changer cet exo il contient la disjonction des cas nous somme pas encore arriver à ça( on peut le faire prochainement), et STP respecte les régles il faut numéroter l'exo et l'ecrire (pas un lien) et spoilerles réponse Amicalement | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 17:51 Sam 30 Juil 2011, 17:51 | |
| Exercice 10:Soient x, y et a des réels. Montrer que: \in%20\mathbb{R}^3):(x^2+y^2=a^2\Rightarrow%20\frac{a^4}{2}\leq%20x^4+y^4\leq%20a^4)) | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 18:40 Sam 30 Juil 2011, 18:40 | |
| - Spoiler:
a²=x²+y² alors a^4/2<=x^4+y^4
a^4<=2(x^4+y^4)
(x²+y²)²<=2(x^4+y^4)
x^4+2x²y²+y^4<=2(x^4+y^4)
2x²y²<=x^4+y^4
x^4+y^4-2x²y²>=0
(x²-y²)²>=0 et ca c'est vrai alors a^4/2<=x^4+y^4
la deuxieme x^4+y^4<=a^4
x^4+y^4<=(x²+y²)²
x^4+y^4<=x^4+2x²y²+y^4
2x²y²>=0et ca c'est vrai alors du 1 et 2 on trouve a^4/2<=x^4+y^4<=a^4
enfin j'aimerais bien savoir si ma reponse est juste
| |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 21:30 Sam 30 Juil 2011, 21:30 | |
| Oui je pense que cela est juste ! Mnt c tn tour de poster  | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 21:41 Sam 30 Juil 2011, 21:41 | |
| merci d'acord voila un exo Exercice 11: soient a,b,x,et y quatres réels dont ax+by=1 demontrez que 1/a²+b²<=x²+y²  | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 21:52 Sam 30 Juil 2011, 21:52 | |
| 1/(a²+b²)<= x²+y²
équiv à : (1-(ax)²-(bx)²-(ay)²-(by)²)/a²+b² <=0
et on a : (ax)²+(by)²+2ax.by=1
donc : ( 1-(ax)²-(bx)²-(ay)²-(by)²)= 2ax.by-(ay)²-(bx)²
on sait que : (ay)²+(bx)² >= 2ax.by
donc : ( 1-(ax)²-(bx)²-(ay)²-(by)²)<=0
et puisque : a²+b²>=0
alors (1-(ax)²-(bx)²-(ay)²-(by)²)/a²+b² <=0
donc 1/a²+b²<=x²+y² | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 22:22 Sam 30 Juil 2011, 22:22 | |
| j'ai une methode plus facile mais ta methode aussi est juste alors c'est ton tour de poser un exo et merci  | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 22:59 Sam 30 Juil 2011, 22:59 | |
| il suffit de remarque que l'inégalité est équivalente à 1=<(a²+b²)(x²+y²)<-->
1=<a²x²+a²y²+b²x²+b²y²=(ax+by)²+(ay-bx)² <--> 0=<(ay-bx)²
cela finit la démonstration .
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 23:36 Sam 30 Juil 2011, 23:36 | |
| Pourquoi personne n'a proposé aucun exo? puisque Sanfoura9 est hors ligne, je crois que c'est à boubou math de proposer un autre exo. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 23:42 Sam 30 Juil 2011, 23:42 | |
| je n'ai pas d'exo de logique intéressant a poster maintenant,j'ai plutôt un exo d’arithmétique, si vous voulez , je le poste . | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  | |
| |
|
  | |
| | Préparation à la première SM (La logique) |  |
|
