| | Préparation à la première SM (La logique) |  |
|
+13Nayssi darkpseudo upsilon az360 expert_run boubou math salimreda sanfoura9 yasserito Ahmed Taha (bis) geom ali-mes Azerty1995 17 participants |
|
| Auteur | Message |
|---|
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 03:38 Mer 03 Aoû 2011, 03:38 | |
| Merci..
Je vous propose cet exercice comme suivant:
Exercice 18
Soit x_{1} et x_{2} et ... et x_{100} cent nombres
Tel que x_{1} + x_{2} + ... + x_{100}=x_{1} *x_{2} * ... * x_{100}
Montrez que au moins 93 de ces nombres est égal à 1 | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 04:04 Mer 03 Aoû 2011, 04:04 | |
| Joli exo (classique de Dima Dima) Un contre exemple: x_i=0 avec i £ {1,2,3,....,100}  Je crois qu'il faut ajouter la condition de: x_i sont des entiers naturels nons nuls. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 | |
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 12:59 Mer 03 Aoû 2011, 12:59 | |
| - ali-mes a écrit:
- Joli exo (classique de Dima Dima)
Un contre exemple: x_i=0 avec i £ {1,2,3,....,100} 
Je crois qu'il faut ajouter la condition de: x_i sont des entiers naturels nons nuls.
Exact.. J'ai oublié la condition que tous ces x appartiennent à IN | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 16:44 Mer 03 Aoû 2011, 16:44 | |
| - az360 a écrit:
- upsilon a écrit:
- Bon d'accord..
Voici donc la demonstration plus clair...
[url= ] ]
Amicalement  Puisque n+1<n !!! ???? Ah oui!!Quelle faute!!   Je ne l'avais apercu, c'est une faute d'inattention.. Donc ma methode est fausse!!!Est ce que quelqu'un pouvait il poster la reponse juste?? | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 16:56 Mer 03 Aoû 2011, 16:56 | |
| | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 18:44 Mer 03 Aoû 2011, 18:44 | |
| Maintenant, On va travailler sur la récurrence. Voici quelques résultats élémentaires: Exercice 18:Montrer par récurrence: 1)- :\;&space;\sum_{i=1}^ni=\frac{n(n+1)}{2}) 2)- :\;&space;\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}{6}) 3)- :\;&space;\sum_{i=1}^ni^3=\left&space;(\frac{n(n+1)}{2}&space;\right&space;)^2) 4)- :\;&space;7\;&space;\mathrm{divise}\;&space;\;&space;3^{2n}-2^n) 5)- :\;&space;11\;&space;\mathrm{divise}\;&space;\;&space;3^{2n}+2^{6n+5})
Dernière édition par ali-mes le Mer 03 Aoû 2011, 22:35, édité 1 fois | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 22:15 Mer 03 Aoû 2011, 22:15 | |
| Solution de l'exercice 18- Spoiler:
1) Pour n=1 on a }{2}=1) ce qui est vrai Supposons que :\;&space;\sum_{i=1}^ni=\frac{n(n+1)}{2}) est montrons que (n+2)}{2}) On a =\frac{n(n+1)}{2}+(n+1)=\frac{(n+1)(n+2)}{2}) Donc :\;&space;\sum_{i=1}^ni=\frac{n(n+1)}{2}) 2) Pour n=1 on a (2+1)}{6}= 1) ce qui est vrai Supposons que :\;&space;\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}{6}) et montrons que (n+2)(2n+3)}{6}) On a ^{2}=\frac{n(n+1)(2n+1)}{6}+(n+1)^{2}=\frac{(n+1)(n(2n+1)+6(n+1))}{6}=\frac{(n+1)(2n^{2}+7n+6)}{6}=\frac{(2n^{2}+4n+3n+6)}{6}=\frac{(n+1)(n+2)(2n+3)}{6}) Donc :\;&space;\sum_{i=1}^ni^2=\frac{n(n+1)(2n+1)}{6}) 3) Pour n=1 on a }{2}&space;\right&space;)^2=1) ce qui est vrai Supposons que :\;&space;\sum_{i=1}^ni^3=\left&space;(\frac{n(n+1)}{2}&space;\right&space;)^2) est montrons que (n+2)}{2}&space;\right&space;)^2) On a ^{3}=(\frac{n(n+1)}{2})^{2}+(n+1)^{3}=\frac{n^{2}(n+1)^{2}+4(n+1)^{3}}{2^{2}}=\frac{(n+1)^{2}(n^{2}+4(n+1))}{2^{2}}=\frac{(n+1)^{2}(n+2)^{2}}{2^{2}}=(\frac{(n+1)(n+2)}{2})^{2}) 4) Pour n=0 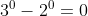 e 7 t divise 0 Donc c'est vraipour n=0 Supposons que 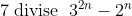 est montrons que 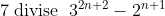 On a ) *3^{n+1}-2*2^{n}=7*3^{n+1}+2*3^{n+1}-2*2^{n}=7(3^{n+1})+2(3^{2n}-2^{n})=7(3^{n+1})+2*7k=7(3^{n+1}+2)) Donc :\;&space;7\;&space;\mathrm{divise}\;&space;\;&space;3^{2n}-2^n) 5) prenons n=0 on trouve -31 divise 11 et c'est faux
pour 5) c'est faux | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 22:33 Mer 03 Aoû 2011, 22:33 | |
| Votre réponse est juste, pour le 5) c'est plutôt (+) à la place de (-), je vais éditer. | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 12:49 Jeu 04 Aoû 2011, 12:49 | |
| Montrer qu'il existe un entier naturel x tels que : (∀n ≥ x) : 2^n ≥ (n+2)²
| |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 14:07 Jeu 04 Aoû 2011, 14:07 | |
| 2^6 ≥ (6+2)2 => alors il existe x ... | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 14:20 Jeu 04 Aoû 2011, 14:20 | |
| avec une démonstration bien sure! | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 14:29 Jeu 04 Aoû 2011, 14:29 | |
| Ce que tu as dis est faux az360 , montrez le par récurrence c'est facile . | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 16:32 Jeu 04 Aoû 2011, 16:32 | |
| - darkpseudo a écrit:
- Ce que tu as dis est faux az360 , montrez le par récurrence c'est facile .
Vous étés sur !!! ??? j’attend votre explication de "faux" . je vois qu'il est vrai .  | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 17:21 Jeu 04 Aoû 2011, 17:21 | |
| Je pense qu'il faut ajouter la donnée que le nombre n est un entier naturel.. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 17:45 Jeu 04 Aoû 2011, 17:45 | |
| - az360 a écrit:
- darkpseudo a écrit:
- Ce que tu as dis est faux az360 , montrez le par récurrence c'est facile .
Vous étés sur !!! ??? j’attend votre explication de "faux" . je vois qu'il est vrai .  Ce que tu as écris c'est juste montrer qu'il existe n tel que 2^(n)>=(n+2)^2 ce qui est demandé c'est prouver qu'il existe x tel que pour tout n>=x on a 2^(n)>=(n+2)^2 , en prenant x=6 c'est vrai et pour le montrer la réccurence est bon moyen ( on peut aussi utilisé les fonctions mais c'est plus pour les terminals ) . Amicalement . | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 17:48 Jeu 04 Aoû 2011, 17:48 | |
| Mr. Az360, ta réponse est plutôt incomplète. Relis bien l'énoncé : Montrer qu' il existe un entier naturel x tels que : ( ∀n ≥ x) : 2^n ≥ (n+2)²  Solution Exercice 18 Solution Exercice 18- Spoiler:
Soit P(n) : 2^n >= (n+2)².
Pour n=6, P(n) est vraie.
Montrons que P(n) => P(n+1) avec n>=6
2^(n+1)=2*(2^n)>2(n+2)²
De plus 2(n+2)²-(n+3)²=n²+2n-1=(n+1)²-1>=48>0
Ainsi 2(n+2)²>(n+3)². D'où l'hérédité.
Ainsi il existe x tel que (∀n>=x),2^n >= (n+3)².
Dernière édition par Nayssi le Jeu 04 Aoû 2011, 21:03, édité 1 fois | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 18:20 Jeu 04 Aoû 2011, 18:20 | |
| ce que tu as écrit c très juste et çà la même méthode que j'ai fait , mais imaginons si ce nombre x n'était pas si facile à trouver comme le 6 , comment pourrait -on résoure cet exo ?? | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 19:37 Jeu 04 Aoû 2011, 19:37 | |
| - darkpseudo a écrit:
- az360 a écrit:
- darkpseudo a écrit:
- Ce que tu as dis est faux az360 , montrez le par récurrence c'est facile .
Vous étés sur !!! ??? j’attend votre explication de "faux" . je vois qu'il est vrai .  Ce que tu as écris c'est juste montrer qu'il existe n tel que 2^(n)>=(n+2)^2 ce qui est demandé c'est prouver qu'il existe x tel que pour tout n>=x on a 2^(n)>=(n+2)^2 , en prenant x=6 c'est vrai et pour le montrer la réccurence est bon moyen ( on peut aussi utilisé les fonctions mais c'est plus pour les terminals ) . Amicalement . Merci ...  amicalement | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 19:39 Jeu 04 Aoû 2011, 19:39 | |
| - Nayssi a écrit:
- Mr. Az360, ta réponse est plutôt incomplète. Relis bien l'énoncé : Montrer qu'il existe un entier naturel x tels que : (∀n ≥ x) : 2^n ≥ (n+2)²

Solution Exercice 18
- Spoiler:
Soit P(n) : 2^n >= (n+3)².(faute d’intention c'est plutot n+2 pas n + 3)
Pour n=6, P(n) est vraie.
Montrons que P(n) => P(n+1) avec n>=6
2^(n+1)=2*(2^n)>2(n+2)²
De plus 2(n+2)²-(n+3)²=n²+2n-1=(n+1)²-1>=48>0
Ainsi 2(n+2)²>(n+3)². D'où l'hérédité.
Ainsi il existe x tel que (∀n>=x),2^n >= (n+3)².
Merci de courrier votre réponse : Soit P(n) : 2^n >= (n+2)². Et Merci pour l'explication !!!  | |
|
  | |
Nayssi
Maître

 Nombre de messages : 235 Nombre de messages : 235
Age : 28
Date d'inscription : 26/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Jeu 04 Aoû 2011, 21:03 Jeu 04 Aoû 2011, 21:03 | |
| Effectivemet. C'est edité! | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 05 Aoû 2011, 03:05 Ven 05 Aoû 2011, 03:05 | |
| Voici un autre exercice pour avancer le jeu: Exercice 19:Le but de l'exercice est de chercher toutes les fonctions qui satisfont ces conditions: i)- f(x) est définie de  vers  . ii)- =f(x)+1\;&space;\;&space;\left&space;(\forall&space;x\in&space;\;&space;\mathbb{Q}^{\ast&space;}_{+}&space;\right&space;)) . iii)- =f(x)^2\;&space;\;&space;\left&space;(\forall&space;x\in&space;\;&space;\mathbb{Q}^{\ast&space;}_{+}&space;\right&space;)) 1)- En utilisant (ii), montrer par récurrence que: \right&space;)(\forall&space;n\;\in&space;\mathbb{N}\ast&space;):&space;\;&space;\;&space;f(x+n)=f(x)+n) 2)- Montrer que: \right&space;)(\forall&space;n\;\in&space;\mathbb{N}\ast&space;):&space;\;&space;\;&space;f(x^2+2nx)=f(x)^2+2nf(x)) . 3)- Vérifier que f n'est pas constante. 4)- Conclure toutes les fonctions qui satisfont la conditions de l'exercice. 5)- Un peu en retard mais quand même, رمضان مبارك كريم  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Ven 05 Aoû 2011, 23:22 Ven 05 Aoû 2011, 23:22 | |
| Pas de réponses ?? - Spoiler:
Je donne des indices:
pour 2)- Remplacer dans (iii) x par x+n.
3)- Utiliser l'absurde.
4)- Utiliser le fait que tout rationnel strictement positif peut s'écrire sous la forme p/q avec p et q des entiers naturels (q non nul).
Et remplacer dans (2) x par p/q et n par q.
| |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 06 Aoû 2011, 02:50 Sam 06 Aoû 2011, 02:50 | |
| Voila la solution de l'exercice que je vous propose,même si un peu en ..retard - Spoiler:
1)On a f(x+1)=f(x)+1Donc f(x+n)=f(x+n-1)+1 =f(x+n-2)+2 =f(x+n-3)+3 et puisque n £ IN Donc il existe un nombre de IN qui est égal à n Ainsi On conclut que f(x+n)= =f(x+n-n)+n=f(x)+n (Cette methode n'est pas basée sur une demonstration précise..) 2) On veut prouver que f(x²+2nx)=f(x²)+2nf(x)On a f(x²+2nx)=f(x²+2nx+n²)-n²=f(x+n)²-n² =[f(x+n)-n] [f(x+n)+n]=f(x)²+2nf(x) 3) Si f est constante Donc f(x)=f(x+1) D'ou f(x)+1=f(x+1)+1 Ce qui est contradiction car f(x)+1 et f(x) ne sont pas égaux D'ou f n'est pas constante 4) On va trouver les fonctions f qui satisfont les conditionOn remplace dans f(x²+2nx)=f(x²)+2nf(x) x par 1/n On a f(1/n²+2)=f(1/n²)+2nf(1/n) Donc f(1/n)²+2 = f(1/n)²+2nf(1/n) D'ou nf(1/n)=1 Ainsi f(1/n)=1/n On pourrait dire que f est identique sur Q*+ Enfin, c'est ce que j'ai trouvé.. 
| |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 07 Aoû 2011, 01:03 Dim 07 Aoû 2011, 01:03 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  | |
| |
|
  | |
| | Préparation à la première SM (La logique) |  |
|
