| | Préparation à la première SM (La logique) |  |
|
+13Nayssi darkpseudo upsilon az360 expert_run boubou math salimreda sanfoura9 yasserito Ahmed Taha (bis) geom ali-mes Azerty1995 17 participants |
|
| Auteur | Message |
|---|
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Sam 30 Juil 2011, 23:32 Sam 30 Juil 2011, 23:32 | |
| Je vous propose quelques exercices de notre premier test en 1bac/M. Exercice 12:Prouvez que: (\exists&space;\alpha&space;%3E0)(\forall&space;x&space;\in&space;\mathbb{R}-\left&space;\{&space;-1&space;\right&space;\})&space;|x-1|%3C\alpha&space;\Rightarrow&space;\left&space;|&space;\frac{1}{x+1}&space;-\frac{1}{2}\right&space;|<&space;\xi) Exercice 13: Exercice 13:Soient a;b et c des entiers relatifs impairs. Prouvez que l'équation ax^(2)+bx+c=0 n'admet aucune solution dans Q. Si vous voulez j'en ai encore d'autres exercices.
Dernière édition par expert_run le Dim 31 Juil 2011, 14:22, édité 1 fois | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 09:44 Dim 31 Juil 2011, 09:44 | |
| EXO12: d'abord,remarquons que }|%3C\xi&space;\Leftrightarrow&space;|\frac{1-x}{2(x+1)}|%3C\xi&space;\Leftrightarrow&space;|1-x|%3C2|x+1|\xi&space;\Leftrightarrow&space;|x-1|%3C2|x+1|\xi) donc il faut prouver que (\exists&space;\alpha&space;%3E0)(\forall&space;x&space;\in&space;\mathbb{R}-\left&space;\{&space;-1&space;\right&space;\})&space;|x-1|%3C\alpha&space;\Rightarrow&space;|x-1|%3C2|x+1|\xi) on sait bien qu'il existe  tels que pour tous 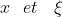 tels que  , cela finit la demonstration . EXO13: pour prouver que l'equation n'admet pas de solution dans Q , il suffit de prouver que 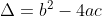 ne peut pas être le carré d'un rationnel . a,b et c sont des entier donc 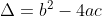 l'est aussi ainsi il faut prouver 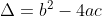 ne peut pas être le carré d'un entier ,autrement dit , il faut prouver que l’équation 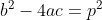 n'admet pas de solution dans IN On a  b² est impair et 4ac est pair alors b²-4ac est impair d'ou p est impair D'une autre part b² est impair alors il est congrue 1 modulo 8 de même p² est congrue 1 modulo 8 ainsi b²-p²est congrue 0 modulo 8d'ou 4ac est congru 0 modulo 8 or cela est impossible car a et c sont impair . cela finit la démonstration . | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 14:46 Dim 31 Juil 2011, 14:46 | |
| C'est juste passant à autre choses donc Exercie14:Prouvez que si m et n sont deux entiers naturels strictement positifs on a:  | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 15:13 Dim 31 Juil 2011, 15:13 | |
| Solution de l'exercice 14- Spoiler:
| |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 15:19 Dim 31 Juil 2011, 15:19 | |
| on commence à résoudre les exos du livre "almoufid" ?? | |
|
  | |
Azerty1995
Expert grade2

 Nombre de messages : 345 Nombre de messages : 345
Age : 29
Date d'inscription : 28/01/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 15:26 Dim 31 Juil 2011, 15:26 | |
| J'ai pas d'exercice à proposer. | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 15:42 Dim 31 Juil 2011, 15:42 | |
| déterminer toutes les fonctions strictement croissantes de lN >lN tel que :
f(m.n)=f(m).f(n) et f(2)=2 quelque soit m et n e lN²
Dernière édition par sanfoura9 le Lun 01 Aoû 2011, 16:54, édité 1 fois | |
|
  | |
salimreda
Maître

 Nombre de messages : 280 Nombre de messages : 280
Age : 29
Localisation : maroc
Date d'inscription : 24/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Dim 31 Juil 2011, 22:43 Dim 31 Juil 2011, 22:43 | |
| voici ma reponse - Spoiler:
f(m.n)=f(m).(n) et f(2)=2 quelque soit m et n e lN²
on a f(m.n)=f(n.m) donc f(m.).n=f(n.).m Poson m =2
on aura
2n=2f(n)
n=f(n)
alors la fonction est f(x)=x
| |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 15:43 Lun 01 Aoû 2011, 15:43 | |
| - salimreda a écrit:
- voici ma reponse
- Spoiler:
f(m.n)=f(m).(n) et f(2)=2 quelque soit m et n e lN²
on a f(m.n)=f(n.m) donc f(m.).n=f(n.).m Poson m =2
on aura
2n=2f(n)
n=f(n)
alors la fonction est f(x)=x
Peux-tu expliquer cette étape de votre "preuve" ? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 15:54 Lun 01 Aoû 2011, 15:54 | |
| C'est une simple symétrie. | |
|
  | |
boubou math
Expert sup
 Nombre de messages : 521 Nombre de messages : 521
Age : 29
Date d'inscription : 23/12/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 16:12 Lun 01 Aoû 2011, 16:12 | |
| - ali-mes a écrit:
- salimreda a écrit:
- voici ma reponse
- Spoiler:
f(m.n)=f(m).(n) et f(2)=2 quelque soit m et n e lN²
on a f(m.n)=f(n.m) donc f(m.).n=f(n.).m Poson m =2
on aura
2n=2f(n)
n=f(n)
alors la fonction est f(x)=x
Peux-tu expliquer cette étape de votre "preuve" ? il a juste remplacer n par m et m par n | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 16:47 Lun 01 Aoû 2011, 16:47 | |
| - boubou math a écrit:
- ali-mes a écrit:
- salimreda a écrit:
- voici ma reponse
- Spoiler:
f(m.n)=f(m).(n) et f(2)=2 quelque soit m et n e lN²
on a f(m.n)=f(n.m) donc f(m.).n=f(n.).m Poson m =2
on aura
2n=2f(n)
n=f(n)
alors la fonction est f(x)=x
Peux-tu expliquer cette étape de votre "preuve" ? il a juste remplacer n par m et m par n
Et pour "f(m.).n=f(n.).m" ? | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 16:53 Lun 01 Aoû 2011, 16:53 | |
| c'est juste l'application de f(m.n)=f(m).(n) | |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 16:54 Lun 01 Aoû 2011, 16:54 | |
| f(m.n) = f(m).f(n) non pas f(m).n ! | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 17:07 Lun 01 Aoû 2011, 17:07 | |
| T'avais écrit f(m.n) = f(m).(n)
| |
|
  | |
sanfoura9
Féru

 Nombre de messages : 38 Nombre de messages : 38
Age : 28
Localisation : SEFROU
Date d'inscription : 29/05/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 17:41 Lun 01 Aoû 2011, 17:41 | |
| c juste une faute de saisie ^^ | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 17:46 Lun 01 Aoû 2011, 17:46 | |
| Ma réponse pour l'exercice 15:- Spoiler:
On cherche toutes les fonctions f strictement croissantes définies de IN vers IN qui satisfont la condition: \in%20\mathbb{N}^2)\;%20\;%20f(m.n)=f(m).f(n)\;%20\;%20\;%20\mathrm{et}\;%20\;%20\;%20f(2)=2) Puisque f est strictement croissante sur IN, donc f est injective. Soit P(m,n) l'assertion: f(m.n)=f(m).f(n) P(1,1)=> f(1.1)=f(1).f(1) => f(1)=f(1)² => f(1)=0 ou f(1)=1 On suppose que f(1)=0, on a donc: P(m,1)=> f(m.1)=f(m).f(1) => f(m)=f(m).0=0 Donc pour tous entier naturel m on a: f(m)=0, ce qui est contradictoire avec le fait que f est injective. On conclut que f(1)=1. De même, on montre que f(0)=0. Maintenant, montrons par récurrence que: :\;%20\;%20f(m)=m) . Clairement, la relation est vérifiée pour m=0 et m=1. Hérédité: On suppose que: :\;%20\;%20f(n)=n) Et on montre que: f(n+1)=n+1. Pour cela, on va faire une petite disjonction de cas: * Si n est est impair, donc (n+1)/2 est pair, donc: 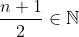 Puisque n est impair et n>1, on a donc n> 2 => 2n-n>2 => 2n>n+2 => 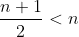 Donc la relation de récurrence est vérifiée pour 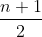 . On a donc: \Rightarrow%20f(2\times%20\frac{n+1}{2})=f(2).f(\frac{n+1}{2})) =2.f(\frac{n+1}{2})) =2\times%20\frac{n+1}{2}) =n+1) . * Si n est pair, donc n+2 est pair, donc: 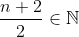 . Et puisque n>2 => 2n-n>2 => 2n>n+2 => n>(n+1)/2. Donc la relation de récurrence est vérifiée pour (n+1)/2. On a donc: \Rightarrow%20f(2\times%20\frac{n+2}{2})=f(2).f(\frac{n+2}{2})) \Rightarrow%20f(n+2)=2.f(\frac{n+2}{2})) =2\times%20\frac{n+2}{2}=n+2) . On a f est strictement croissante donc: f(n+2)>f(n+1) et f(n+1)>f(n). Et puisque f(n+2)=n+2 et f(n)=n et n+2>n+1>n. On conclut que f(n+1)=n+1. Dans les deux cas (n est pair et n est impair) on a: f(n+1)=n+1. Synthèse de la récurrence: Pour tous entier naturel n on a: f(n)=n. Réciproquement, considérons la fonction f: IN ->IN f(n)=n. On a: * f est strictement croissante sur IN. * f(m)=m et f(n)=n donc f(m)f(n)=mn et f(mn)=mn d'où: f(m)f(n)=f(mn). Donc la seule fonction qui satisfait la condition de l'exercice est l'identique sur IN.
Exercice 16: (l'absurde) Considérons l'ensemble: A={1,2,...,n} tel que n est un entier naturel impair. Soient x_{1} et x_{2} et ... et x_{n} des éléments de A distincts. Montrer qu'il existe un élément k de A tel que x_{k}-k soit pair. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 18:52 Lun 01 Aoû 2011, 18:52 | |
| - ali-mes a écrit:
- Ma réponse pour l'exercice 15:
- Spoiler:
On cherche toutes les fonctions f strictement croissantes définies de IN vers IN qui satisfont la condition: \in%20\mathbb{N}^2)\;%20\;%20f(m.n)=f(m).f(n)\;%20\;%20\;%20\mathrm{et}\;%20\;%20\;%20f(2)=2) Puisque f est strictement croissante sur IN, donc f est injective. Soit P(m,n) l'assertion: f(m.n)=f(m).f(n) P(1,1)=> f(1.1)=f(1).f(1) => f(1)=f(1)² => f(1)=0 ou f(1)=1 On suppose que f(1)=0, on a donc: P(m,1)=> f(m.1)=f(m).f(1) => f(m)=f(m).0=0 Donc pour tous entier naturel m on a: f(m)=0, ce qui est contradictoire avec le fait que f est injective. On conclut que f(1)=1. De même, on montre que f(0)=0. Maintenant, montrons par récurrence que: :\;%20\;%20f(m)=m) . Clairement, la relation est vérifiée pour m=0 et m=1. Hérédité: On suppose que: :\;%20\;%20f(n)=n) Et on montre que: f(n+1)=n+1. Pour cela, on va faire une petite disjonction de cas: * Si n est est impair, donc (n+1)/2 est pair, donc: 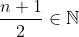 Puisque n est impair et n>1, on a donc n> 2 => 2n-n>2 => 2n>n+2 => 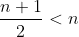 Donc la relation de récurrence est vérifiée pour 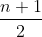 . On a donc: \Rightarrow%20f(2\times%20\frac{n+1}{2})=f(2).f(\frac{n+1}{2})) =2.f(\frac{n+1}{2})) =2\times%20\frac{n+1}{2}) =n+1) . * Si n est pair, donc n+2 est pair, donc: 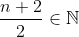 . Et puisque n>2 => 2n-n>2 => 2n>n+2 => n>(n+1)/2. Donc la relation de récurrence est vérifiée pour (n+1)/2. On a donc: \Rightarrow%20f(2\times%20\frac{n+2}{2})=f(2).f(\frac{n+2}{2})) \Rightarrow%20f(n+2)=2.f(\frac{n+2}{2})) =2\times%20\frac{n+2}{2}=n+2) . On a f est strictement croissante donc: f(n+2)>f(n+1) et f(n+1)>f(n). Et puisque f(n+2)=n+2 et f(n)=n et n+2>n+1>n. On conclut que f(n+1)=n+1. Dans les deux cas (n est pair et n est impair) on a: f(n+1)=n+1. Synthèse de la récurrence: Pour tous entier naturel n on a: f(n)=n. Réciproquement, considérons la fonction f: IN ->IN f(n)=n. On a: * f est strictement croissante sur IN. * f(m)=m et f(n)=n donc f(m)f(n)=mn et f(mn)=mn d'où: f(m)f(n)=f(mn). Donc la seule fonction qui satisfait la condition de l'exercice est l'identique sur IN.
Exercice 16: (l'absurde)
Considérons l'ensemble: A={1,2,...,n} tel que n est un entier naturel impair.
Soient x_{1} et x_{2} et ... et x_{n} des éléments de A distincts.
Montrer qu'il existe un élément k de A tel que x_{k}-k soit pair. Pour perfectionner la preuve, il faut prouver que f est surjective pour conclure la patie f(n+1)=n+1 lorsque n est pair, ce qui est facile à démontrer. | |
|
  | |
az360
Expert grade2

 Nombre de messages : 312 Nombre de messages : 312
Age : 30
Localisation : agadir
Date d'inscription : 28/11/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Lun 01 Aoû 2011, 23:57 Lun 01 Aoû 2011, 23:57 | |
| - ali-mes a écrit:
- Ma réponse pour l'exercice 15:
- Spoiler:
On cherche toutes les fonctions f strictement croissantes définies de IN vers IN qui satisfont la condition: \in%20\mathbb{N}^2)\;%20\;%20f(m.n)=f(m).f(n)\;%20\;%20\;%20\mathrm{et}\;%20\;%20\;%20f(2)=2) Puisque f est strictement croissante sur IN, donc f est injective. Soit P(m,n) l'assertion: f(m.n)=f(m).f(n) P(1,1)=> f(1.1)=f(1).f(1) => f(1)=f(1)² => f(1)=0 ou f(1)=1 On suppose que f(1)=0, on a donc: P(m,1)=> f(m.1)=f(m).f(1) => f(m)=f(m).0=0 Donc pour tous entier naturel m on a: f(m)=0, ce qui est contradictoire avec le fait que f est injective. On conclut que f(1)=1. De même, on montre que f(0)=0. Maintenant, montrons par récurrence que: :\;%20\;%20f(m)=m) . Clairement, la relation est vérifiée pour m=0 et m=1. Hérédité: On suppose que: :\;%20\;%20f(n)=n) Et on montre que: f(n+1)=n+1. Pour cela, on va faire une petite disjonction de cas: * Si n est est impair, donc (n+1)/2 est pair, donc: 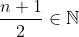 Puisque n est impair et n>1, on a donc n> 2 => 2n-n>2 => 2n>n+2 => 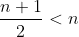 Donc la relation de récurrence est vérifiée pour 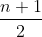 . On a donc: \Rightarrow%20f(2\times%20\frac{n+1}{2})=f(2).f(\frac{n+1}{2})) =2.f(\frac{n+1}{2})) =2\times%20\frac{n+1}{2}) =n+1) . * Si n est pair, donc n+2 est pair, donc: 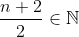 . Et puisque n>2 => 2n-n>2 => 2n>n+2 => n>(n+1)/2. Donc la relation de récurrence est vérifiée pour (n+1)/2. On a donc: \Rightarrow%20f(2\times%20\frac{n+2}{2})=f(2).f(\frac{n+2}{2})) \Rightarrow%20f(n+2)=2.f(\frac{n+2}{2})) =2\times%20\frac{n+2}{2}=n+2) . On a f est strictement croissante donc: f(n+2)>f(n+1) et f(n+1)>f(n). Et puisque f(n+2)=n+2 et f(n)=n et n+2>n+1>n. On conclut que f(n+1)=n+1. Dans les deux cas (n est pair et n est impair) on a: f(n+1)=n+1. Synthèse de la récurrence: Pour tous entier naturel n on a: f(n)=n. Réciproquement, considérons la fonction f: IN ->IN f(n)=n. On a: * f est strictement croissante sur IN. * f(m)=m et f(n)=n donc f(m)f(n)=mn et f(mn)=mn d'où: f(m)f(n)=f(mn). Donc la seule fonction qui satisfait la condition de l'exercice est l'identique sur IN.
Exercice 16: (l'absurde)
Considérons l'ensemble: A={1,2,...,n} tel que n est un entier naturel impair.
Soient x_{1} et x_{2} et ... et x_{n} des éléments de A distincts.
Montrer qu'il existe un élément k de A tel que x_{k}-k soit pair. Je répond : Supposons que : quelque soit k de A on a toujours x_{k} - k impair . alors on fait une petite some on aura : 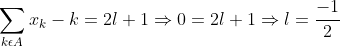 ce qui contradiction ... | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mar 02 Aoû 2011, 00:51 Mar 02 Aoû 2011, 00:51 | |
| Voici trois méthodes pour résoudre ce joli exo: Ma réponse pour l'exercice 16:- Spoiler:
Par l'absurde, supposons que pour tout k de A, on a x_{k}-k. Donc:
- x_{1}-1 est impair => x_{1} est pair
- x_{2}-2 est impair => x_{2} est impair
- x_{3}-3 est impair => x_{3} est pair
Et ainsi de suite, jusqu'à:
- x_{n}-n est impair => x_{n} est pair (car n est impair)
Donc l'ensemble {x_{1}, x_{2}, x_{3}, .... , x_{n}}=A contient plus d'éléments pairs que d'éléments impairs.
Et puisque A={1, 2, .... , n} et n est impair, on conclut que l'ensemble A contient plus d'éléments impairs que d'élément pairs.
Donc contradiction, d'où: il existe un élément k de A tel que x_{k}-k soit pair.
- Spoiler:
Par l'absurde, supposons que pour tout k de A, on a x_{k}-k. Donc:
- x_{1}-1 est impair.
- x_{2}-2 est impair.
- x_{3}-3 est impair.
Et ainsi de suite, jusqu'à:
- x_{n}-n est impair.
On fait la somme, et puisque il y a n nombre impair (et n est impair), donc la somme sera un nombre impair.
Et on a: {x_{1}, x_{2}, x_{3}, .... , x_{n}}=A
Donc:
x_{1}+x_{2}+x_{3}+.....+x_{n}-(1+2+3+.....+n)=0
Donc 0 est impair.
Donc contradiction, d'où: il existe un élément k de A tel que x_{k}-k soit pair.
- Spoiler:
Sans l'absurde, puisque: {x_{1}, x_{2}, x_{3}, .... , x_{n}}=A
On a:
(x_{1}-1)+(x_{2})+(x_{3}-3)+....+(x_{n}-n)=(x_{1}+x_{2}+x_{3}+.....+x_{n})-(1+2+3+.....+n)=0
Donc la somme des nombres (n nombres avec n impair): x_{1}-1 et x_{2}-2 et x_{3}-3 et ..... et x_{n}-n est un nombre pair.
Donc l'un de ces nombres est nécessairement pair.
D'où: il existe un élément k de A tel que x_{k}-k soit pair.
Exercice 17:Montrer par équivalences que: :\;&space;\;&space;(1-\frac{1}{n^2})^n(1+\frac{1}{n})<&space;1) | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mar 02 Aoû 2011, 01:08 Mar 02 Aoû 2011, 01:08 | |
| La deuxième méthode est la même méthode de az360, juste reformulé. | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 02:21 Mer 03 Aoû 2011, 02:21 | |
| - ali-mes a écrit:
Exercice 17:
Montrer par équivalences que: :\;&space;\;&space;(1-\frac{1}{n^2})^n(1+\frac{1}{n})<&space;1) Voici une solution basée sur l'équivalence (1-1/n²)^n(1+1/n)<1 Equiv.à [(n²-1)^n(n+1)]/n^(2n+1)<1 Equiv.à (n²-1)^n(n+1)<n^(2n+1) Equiv.à [ (n²-1)^n](n+1)<n^(2n)*n On sait que n²-1<n² donc (n²-1)^n<(n²)^n Et puisque n+1<n Donc [ (n²-1)^n](n+1)<n^(2n)*n Ce qui finit la demonstration.. | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 02:24 Mer 03 Aoû 2011, 02:24 | |
| Pourriez vous réécrire votre réponse en Latex, car c'est vraimant pas clair. | |
|
  | |
upsilon
Maître

 Nombre de messages : 83 Nombre de messages : 83
Age : 28
Localisation : Fès
Date d'inscription : 19/06/2011
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 02:59 Mer 03 Aoû 2011, 02:59 | |
| Bon d'accord.. Voici donc la demonstration plus clair... [url=  ] Amicalement  | |
|
  | |
ali-mes
Expert sup
 Nombre de messages : 986 Nombre de messages : 986
Age : 28
Localisation : Tétouan
Date d'inscription : 01/10/2010
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  Mer 03 Aoû 2011, 03:08 Mer 03 Aoû 2011, 03:08 | |
| Superbe Upsilon !
Maintenant, c'est ton tour pour proposer un autre exo. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparation à la première SM (La logique) Sujet: Re: Préparation à la première SM (La logique)  | |
| |
|
  | |
| | Préparation à la première SM (La logique) |  |
|
