| | direction mp mp* |  |
|
+11MohE Saiichi aissa expert_run kalm seledeur tahasinbad abdelbaki.attioui Mehdi.O nmo galillee56 15 participants |
|
| Auteur | Message |
|---|
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 13:47 Jeu 01 Aoû 2013, 13:47 | |
| - abdelbaki.attioui a écrit:
- en fait c'est (pk)! non pk! car c'est facile de voir som(k=0..inf, z^(pk)/(pk!))=1/p exp(z^p)
soit f(z)=som(k=0..inf, z^(pk)/(pk)! f est analytique ==> C infini
f^(p)(z)=som(k=1..inf, z^(pk-p)/(pk-p)!=som(k=0..inf, z^(pk)/(pk)!=f(z)
==> f solution de l'éq. diff. linéaire y^(p)-y=0 .
les racines de l'q. caractéristique sont les racines p ième de l'unité, {1,µ, µ²,...,µ^(p-1)}
où µ=exp(2i pi /p) ,
==> f(z)= som(k=0 ..p-1) a_k exp(µ^k z)
On calcule les a_k en calculant f^(k)(0) pour k=0,..,p-1
f(0)=1 ==> a_0+a_1+...+a_(p-1)=1
f'(0)=0 ==> a_0+µ a_1+...+µ^(p-1)a_(p-1)=0
f''(0)=0 ==> a_0+µ² a_1+...+µ^2(p-1)a_(p-1)=0
...
f^(p-1)(0)=0 ==> a_0+µ^(p-1) a_1+...+µ^(p-1)²a_(p-1)=0
Soit V= la matrice de taille pxp (µ^(ij)) _0=<i,j=<p-1 et a =( a_0 a1 ... a_(p-1)) et b=(1 0 ... 0)
Le système devient Va=b Vandermonde ==> a=V^(-1)b
Le calcul de V^(-1) et bien connu tres joli solution Mr.attioui je propose celle ci: soit w=exp(2ipi/p)     | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 14:14 Jeu 01 Aoû 2013, 14:14 | |
| Exo 28:
soit A dans Mn(R) et V1...Vn n colonne
D=det(V1,V2...,Vn)
montrer que som(det(V1..,AVi,..Vn),i=1..n)=tr(A)D | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 15:28 Jeu 01 Aoû 2013, 15:28 | |
| - galillee56 a écrit:
- pour le 24:
je propose ceci
il evident qu une nilpotente verifie
soit A une matrice qui verife pour tout k tr(A^k)=0 notons a_i ses valeurs propre si ils sont tous egaux a_i=0 evident sinon soit a_1...a_j les valeur 2 a 2 distincte
on a pour tout k dans N som(q_ia_i^k,i=1..j)=0 q_i etant la multiplicite de a_i soit P un polynome qui s 'annulle sur a_1...a_{j-1} il est evident qu il s'annule sur a_j donc il existe p tel a_j=a_p donc il sont tous egaux et valent 0 est semblable a une triangulaire superieur strict et c'est gagne
pas pour moi ! | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 15:33 Jeu 01 Aoû 2013, 15:33 | |
| - manazerty a écrit:
- galillee56 a écrit:
- pour le 24:
je propose ceci
il evident qu une nilpotente verifie
soit A une matrice qui verife pour tout k tr(A^k)=0 notons a_i ses valeurs propre si ils sont tous egaux a_i=0 evident sinon soit a_1...a_j les valeur 2 a 2 distincte
on a pour tout k dans N som(q_ia_i^k,i=1..j)=0 q_i etant la multiplicite de a_i soit P un polynome qui s 'annulle sur a_1...a_{j-1} il est evident qu il s'annule sur a_j donc il existe p tel a_j=a_p donc il sont tous egaux et valent 0 est semblable a une triangulaire superieur strict et c'est gagne
pas pour moi ! ok je detail ^^ soit A une nilpotente son polynome caracteristique et P(X)=X^n donc A est trigonalisable et semblable a une triangulaire superieur strict puisque elle pour unique valeur propre 0 pour A^k la diagonal comporte que des 0 et c est gagne | |
|
  | |
manazerty
Maître
 Nombre de messages : 123 Nombre de messages : 123
Date d'inscription : 29/06/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 15:38 Jeu 01 Aoû 2013, 15:38 | |
| | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 16:20 Jeu 01 Aoû 2013, 16:20 | |
| - galillee56 a écrit:
- Exo 28:
soit A dans Mn(R) et V1...Vn n colonne
D=det(V1,V2...,Vn)
montrer que som(det(V1..,AVi,..Vn),i=1..n)=tr(A)D l'application f : (x1,x2...,xn) --> som(det(x1..,Axi,..xn),i=1..n) est une forme n-linéaire alternée de R^n ===> il existe a dans R : f=aD ==> a=trace(A) ( on applique l'unicité de D à une constante multiplicative prés) | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 01 Aoû 2013, 17:31 Jeu 01 Aoû 2013, 17:31 | |
| - abdelbaki.attioui a écrit:
- galillee56 a écrit:
- Exo 28:
soit A dans Mn(R) et V1...Vn n colonne
D=det(V1,V2...,Vn)
montrer que som(det(V1..,AVi,..Vn),i=1..n)=tr(A)D
l'application f : (x1,x2...,xn) --> som(det(x1..,Axi,..xn),i=1..n) est une forme n-linéaire alternée de R^n ===> il existe a dans R : f=aD ==> a=trace(A)
( on applique l'unicité de D à une constante multiplicative prés)
j ai pas bien saisi votre methode comment vous passer de la 1er a la 2em implication et de la 2em a la 3em | |
|
  | |
aissa
Modérateur
 Nombre de messages : 640 Nombre de messages : 640
Age : 64
Localisation : casa
Date d'inscription : 30/09/2006
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 02 Aoû 2013, 04:08 Ven 02 Aoû 2013, 04:08 | |
| l'ensemble des applications n linéaires alternées est un espace vectoriel de dimension 1 (det) on est une base.
tu pend l'image de :(v_1,v_2,....v_n) = (e_1,e_2,...,e_n) la base canonique de M_n,1(IK)
bon courage | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 02 Aoû 2013, 15:06 Ven 02 Aoû 2013, 15:06 | |
| ah d'accord joli methode la mienne consistait a ecrire chaque V_i en fonction des X_i avec les X_i qui sont des vecteur propre et on conclue mais j aime bien votre methode  | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Ven 02 Aoû 2013, 15:16 Ven 02 Aoû 2013, 15:16 | |
| Exo 29:etudier d'apres les valeurs de a et b la convergence de la serie de terme general:  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 14:32 Sam 03 Aoû 2013, 14:32 | |
| - galillee56 a écrit:
- Exo 29:
etudier d'apres les valeurs de a et b la convergence de la serie de terme general:
 ***Soit premièrement la fonction 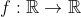 définie ainsi: : f(t)=\int_{0}^{\frac{\pi}{2}}\cos^t(x)dx) . Et notons aussi: 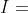 ] 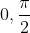 [. ---Si t tend vers  , On a : \cos^t(x)=e^{t.\ln(\cos(x))}\le1) , car : \ln(\cos(x))\le\ln(1)=0) . Ainsi l'intégrale converge dans ce cas. ---Si t tend vers  , On a : \cos^t(x)=e^{t.\ln(\cos(x))}=1+t.\ln(\cos(x))+o(t)) . On a )dx=-\int_{1}^{0}\frac{\ln(y)}{\sqrt{1-y^2}}dy=\int_{0}^{1}\frac{\ln(y)}{\sqrt{1-y^2}}dy) . Au voisinage de 0, on a }{\sqrt{1-y^2}}=\ln(y).(1-y^2)^{-\frac{1}{2}}=\ln(y).(1+\frac{1}{2}y^2+o(y^2))) . Donc l'intégrale }{\sqrt{1-y^2}}dy) converge au voisinage de 0... Au voisinage de 1, on a }{\sqrt{1-y^2}}=\frac{\ln(1+y-1)}{\sqrt{1-y}.\sqrt{1+y}}=\frac{y-1+o(y)}{\sqrt{1+y}.\sqrt{1-y}}=-\frac{\sqrt{y-1}}{\sqrt{y+1}}+o(y)) . Donc l'intégrale }{\sqrt{1-y^2}}dy) converge au voisinage de 0... Ainsi ,l'intégrale converge aussi dans ce cas. ***Revenons à l'exercice proposé: La limite de ) quand n tend vers  est ou bien 0, ou bien  . Et dans tous les cas, la série _{n\in\mathbb{N}}) converge. Sauf erreurs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 15:01 Sam 03 Aoû 2013, 15:01 | |
| En attente d'une confirmation, je propose l'exercice suivant: Exercice 30:Montrer qu'il existe une base de ) constituée de matrices inversibles. PS: L'exercice est tiré d'un Oral Banque Mine-Ponts (2013). | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 15:50 Sam 03 Aoû 2013, 15:50 | |
| | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 16:29 Sam 03 Aoû 2013, 16:29 | |
| - expert_run a écrit:
- L'intégrale converge mais pourquoi la série?
J'ai cru que le problème est d'étudier la convergence de la suite, c'est de ma faute. Le problème demeure donc sans solution... | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 16:35 Sam 03 Aoû 2013, 16:35 | |
| - nmo a écrit:
- expert_run a écrit:
- L'intégrale converge mais pourquoi la série?
J'ai cru que le problème est d'étudier la convergence de la suite, c'est de ma faute.
Le problème demeure donc sans solution... De la même façon que l'intégrale de Wallis on montre que f(t) est équivalente au vois de l'infini à sqrt(pi/(2t)) reste le cas quand t tend vers 0. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 16:59 Sam 03 Aoû 2013, 16:59 | |
| - nmo a écrit:
- En attente d'une confirmation, je propose l'exercice suivant:
Exercice 30:
Montrer qu'il existe une base de ) constituée de matrices inversibles. constituée de matrices inversibles.
PS: L'exercice est tiré d'un Oral Banque Mine-Ponts (2013). en attendant une réponse a l'exo 29 je propose ceci pour l'exo 30 montrons que la famille (I+E_{i,j}) est libre supposons qu'elle liee c a dire qu il existe a_i,j tel sum(a_{i,j}(I+E_{i,j} (i,j) different de (i0,j0))=a_{i0,j0}(I+E_{i0+j0}) i0 differente de j0 en ecrivant la matrice a_(i0,j0)=0 il ne reste plus que les terme pour les quels i=j sum(a_{i,i}(I+E_{i,i}))=a_{i0,i0}(I+E_{i0,i0}) on trouve que les a_(i,i}=-a_{i0,i0} i different de i0 et la somme des a_{i,i} i different de i0 = 2a_{i0,i0} a_i0=0 donc ils sont tous nul la famille est libre bon cardinal c'est une base et tous les elements sont inversible | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 17:07 Sam 03 Aoû 2013, 17:07 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 17:16 Sam 03 Aoû 2013, 17:16 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 17:28 Sam 03 Aoû 2013, 17:28 | |
| Exo31: soit:  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 | |
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Sam 03 Aoû 2013, 19:14 Sam 03 Aoû 2013, 19:14 | |
| - expert_run a écrit:
- galillee56 a écrit:
- Exo31: soit:
 ^{-1}=\sum_{i=1}^{+\infty&space;}\frac{1}{p^{i}_{k}}\Rightarrow&space;\prod_{k=1}^{n}(1-\frac{1}{p_{k}})^{-1}=\prod_{k=1}^{n}\sum_{i=1}^{+\infty&space;}\frac{1}{p^{i}_{k}}=\sum_{i\epsilon&space;S}^{.}\frac{1}{i})
Avec S est l'ensemble des entiers dont la décomposition en facteurs premiers ne contient que des p_i.
alors
^{-1}-\sum_{i=1}^{n}\frac{1}{i}=\sum_{i\epsilon&space;s;i>n}^{.}\frac{1}{i}\leq&space;\sum_{i=n+1}^{+\infty&space;}\frac{1}{i}\Rightarrow&space;r_{n}\sim&space;1/\sum_{i=1}^{n}\frac{1}{i}\sim&space;1/ln(n)) bien joue expert-run bon voici un exo que j'aime bien Exo32:On decoupe un rectangle en plusieurs rectangles de longueur ou de largeur rationelle montrer que le rectangle a soit une largeur ou une longueur rationelle  | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Dim 04 Aoû 2013, 00:50 Dim 04 Aoû 2013, 00:50 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Dim 04 Aoû 2013, 01:03 Dim 04 Aoû 2013, 01:03 | |
| - Vz a écrit:
- On suppose qu'un fourmi commence son chemin d'un sommet du rectangle
 , on définit alors son parcours de la façon suivante, sa prochaine position , on définit alors son parcours de la façon suivante, sa prochaine position  est le sommet d'un sous rectangle du rectangle initial telle que la longueur du côté est le sommet d'un sous rectangle du rectangle initial telle que la longueur du côté  soit rationnelle, le point soit rationnelle, le point  existe à priori d'après les contraintes imposées par l'énoncé, de même on définit la position existe à priori d'après les contraintes imposées par l'énoncé, de même on définit la position  de la même façon, sa dernière position de la même façon, sa dernière position  sera alors la position pour laquelle le point sera alors la position pour laquelle le point  mène à l’extérieur du rectangle, donc le point mène à l’extérieur du rectangle, donc le point  appartient nécessairement à l'un des côtés du rectangle initial qui définit soit une largeur soit une longueur du rectangle initial, la longueur du chemin parcouru est rationnelle par construction, quitte à retirer les montées ou les translations selon la nature du côté précédant on garde une distance toujours rationnelle puisque par construction les montées et les translations sont également rationnelles ,on voit donc immédiatement que la largeur ou la longueur du rectangle est rationnelle appartient nécessairement à l'un des côtés du rectangle initial qui définit soit une largeur soit une longueur du rectangle initial, la longueur du chemin parcouru est rationnelle par construction, quitte à retirer les montées ou les translations selon la nature du côté précédant on garde une distance toujours rationnelle puisque par construction les montées et les translations sont également rationnelles ,on voit donc immédiatement que la largeur ou la longueur du rectangle est rationnelle  Bonsoir, selon votre raisonnement la longueur "et" la largeur sont rationnelles  non ? | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Dim 04 Aoû 2013, 01:10 Dim 04 Aoû 2013, 01:10 | |
| - Mehdi.O a écrit:
- Vz a écrit:
- On suppose qu'un fourmi commence son chemin d'un sommet du rectangle
 , on définit alors son parcours de la façon suivante, sa prochaine position , on définit alors son parcours de la façon suivante, sa prochaine position  est le sommet d'un sous rectangle du rectangle initial telle que la longueur du côté est le sommet d'un sous rectangle du rectangle initial telle que la longueur du côté  soit rationnelle, le point soit rationnelle, le point  existe à priori d'après les contraintes imposées par l'énoncé, de même on définit la position existe à priori d'après les contraintes imposées par l'énoncé, de même on définit la position  de la même façon, sa dernière position de la même façon, sa dernière position  sera alors la position pour laquelle le point sera alors la position pour laquelle le point  mène à l’extérieur du rectangle, donc le point mène à l’extérieur du rectangle, donc le point  appartient nécessairement à l'un des côtés du rectangle initial qui définit soit une largeur soit une longueur du rectangle initial, la longueur du chemin parcouru est rationnelle par construction, quitte à retirer les montées ou les translations selon la nature du côté précédant on garde une distance toujours rationnelle puisque par construction les montées et les translations sont également rationnelles ,on voit donc immédiatement que la largeur ou la longueur du rectangle est rationnelle appartient nécessairement à l'un des côtés du rectangle initial qui définit soit une largeur soit une longueur du rectangle initial, la longueur du chemin parcouru est rationnelle par construction, quitte à retirer les montées ou les translations selon la nature du côté précédant on garde une distance toujours rationnelle puisque par construction les montées et les translations sont également rationnelles ,on voit donc immédiatement que la largeur ou la longueur du rectangle est rationnelle  Bonsoir, selon votre raisonnement la longueur "et" la largeur sont rationnelles :Dnon ? Si le fourmi arrive dans la largeur du rectangle alors sa longueur serait égale à la somme des montées qui est rationnelle par construction, sinon il arrivera dans la longueur du rectangle et sa largeur serait donc égale à la somme des translations...çe serait ton cas si le fourmi arrive au sommet du rectangle qui lie diagonalement le sommet initial, j'ai oublié d'imposer au parcours le fait que le fourmi ne peut se déplacer que dans un seul sens, c'est à dire soit il se déplace à gauche (translation) soit il monte (montée)... | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Dim 04 Aoû 2013, 01:18 Dim 04 Aoû 2013, 01:18 | |
|
Dernière édition par Mehdi.O le Dim 04 Aoû 2013, 01:49, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  | |
| |
|
  | |
| | direction mp mp* |  |
|
