| | direction mp mp* |  |
|
+11MohE Saiichi aissa expert_run kalm seledeur tahasinbad abdelbaki.attioui Mehdi.O nmo galillee56 15 participants |
|
| Auteur | Message |
|---|
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Dim 04 Aoû 2013, 01:26 Dim 04 Aoû 2013, 01:26 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 14:23 Lun 05 Aoû 2013, 14:23 | |
| Vz pourrez vous nous donner des indications parce que personnellement je bug en attendant voici un nouvel exo Exo34: | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 16:47 Lun 05 Aoû 2013, 16:47 | |
| - galillee56 a écrit:
- Vz pourrez vous nous donner des indications parce que personnellement je bug
en attendant voici un nouvel exo
Exo34:
 Salam, Voici ma solution à cet exercice : 1) On Note B_n ce polynôme, il est clair que B_n(X+1)=B_n(X)+B_(n-1)(X) (1), on fixe y et on considère le polynôme B_n(X+y) et le polynôme :  , ces deux ont le même degré qui est n et le même coefficient dominant, donc pour qu'ils soient egaux, il suffit qu'ils aient même valeur pour X€{0,1,..,n-1}, ce qui peut être facilement vérifié par une récurrence finie sur X, tout en utilisant la formule (1). 2) On considère l'endomorphisme f sur IR_n[X] défini par: f(P)(X)=P(x+1), celui-ci est clairement un automorphisme ( sa réciproque est f^-1(P)(X)=P(X-1)) ,la matrice de f dans la base canonique de IR_n[X] est :  , son inverse est :  , et ainsi si on note A la matrice ligne formée par a_0,..,a_n et B la matrice ligne formée par b_0,..,b_n , on a : A=B.M=> B=A.M^-1, d'où le résultat. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 18:31 Lun 05 Aoû 2013, 18:31 | |
| bien joue mehdi.o exo35: | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 19:25 Lun 05 Aoû 2013, 19:25 | |
| - galillee56 a écrit:
- bien joue mehdi.o
exo35:
 Je propose ma solution: Il est très bien connu que les deux fonctions 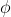 et 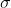 sont multiplicatives. Il suffit pour cela de comparer ces quantités lorsque  où 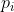 est premier et 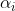 est un entier positif. On dispose des formules: =\sigma(p_i^{\alpha_i})=\frac{p_i^{\alpha_i+1}-1}{p_i-1}) et =\phi(p_i^{\alpha_i})=(p_i-1)p_i^{\alpha_i-1}) . On a .\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}(p_i-1).p_i^{\alpha_i-1}<p_i^{2\alpha_i}=n^2) , ce qui dit que: .\phi(n)}<n) . Et on a +\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}+(p_i-1).p_i^{\alpha_i-1}\ge2\sqrt{p_i^{\alpha_i-1}.(p_i^{\alpha_i+1}-1)}>2\sqrt{p_i^{2\alpha_i}}=2n) , donc +\phi(n)}{2}>n) . On a donc pour  , les inégalités: +\phi(n)}{2}>n>\sqrt{\sigma(n).\phi(n)}) . On retient les mêmes comparaisons pour n'importe quel entiers. Sauf erreurs. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 19:31 Lun 05 Aoû 2013, 19:31 | |
| - galillee56 a écrit:
- nmo a écrit:
- En attente d'une confirmation, je propose l'exercice suivant:
Exercice 30:
Montrer qu'il existe une base de ) constituée de matrices inversibles. constituée de matrices inversibles.
PS: L'exercice est tiré d'un Oral Banque Mine-Ponts (2013). en attendant une réponse a l'exo 29 je propose ceci pour l'exo 30
montrons que la famille (I+E_{i,j}) est libre supposons qu'elle liee c a dire qu il existe a_i,j tel sum(a_{i,j}(I+E_{i,j} (i,j) different de (i0,j0))=a_{i0,j0}(I+E_{i0+j0}) i0 differente de j0 en ecrivant la matrice a_(i0,j0)=0 il ne reste plus que les terme pour les quels i=j sum(a_{i,i}(I+E_{i,i}))=a_{i0,i0}(I+E_{i0,i0}) on trouve que les a_(i,i}=-a_{i0,i0} i different de i0 et la somme des a_{i,i} i different de i0 = 2a_{i0,i0} a_i0=0 donc ils sont tous nul la famille est libre bon cardinal c'est une base et tous les elements sont inversible L'idée est bonne. Mais ce n'est pas celle que j'attendais... En attendant une confirmation de la solution précédente, je propose cet exercice: Exercice 36:Montrer que l'ensemble ) est dense dans ) . Et retrouver ensuite le résultat de l'exercice 30. Bonne chance. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 20:11 Lun 05 Aoû 2013, 20:11 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 20:50 Lun 05 Aoû 2013, 20:50 | |
| Sinon, voilà une preuve à cette inégalité dans le cas général : On pose  ,l'inégalité à démontrer est :  , qui est équivalente à :  or les alpha_i sont tous supérieurs à 1, donc :  . D'où le résultat.
Dernière édition par Mehdi.O le Lun 05 Aoû 2013, 22:15, édité 1 fois | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 21:46 Lun 05 Aoû 2013, 21:46 | |
| - nmo a écrit:
- galillee56 a écrit:
- nmo a écrit:
- En attente d'une confirmation, je propose l'exercice suivant:
Exercice 30:
Montrer qu'il existe une base de ) constituée de matrices inversibles. constituée de matrices inversibles.
PS: L'exercice est tiré d'un Oral Banque Mine-Ponts (2013). en attendant une réponse a l'exo 29 je propose ceci pour l'exo 30
montrons que la famille (I+E_{i,j}) est libre supposons qu'elle liee c a dire qu il existe a_i,j tel sum(a_{i,j}(I+E_{i,j} (i,j) different de (i0,j0))=a_{i0,j0}(I+E_{i0+j0}) i0 differente de j0 en ecrivant la matrice a_(i0,j0)=0 il ne reste plus que les terme pour les quels i=j sum(a_{i,i}(I+E_{i,i}))=a_{i0,i0}(I+E_{i0,i0}) on trouve que les a_(i,i}=-a_{i0,i0} i different de i0 et la somme des a_{i,i} i different de i0 = 2a_{i0,i0} a_i0=0 donc ils sont tous nul la famille est libre bon cardinal c'est une base et tous les elements sont inversible L'idée est bonne. Mais ce n'est pas celle que j'attendais...
En attendant une confirmation de la solution précédente, je propose cet exercice:
Exercice 36:
Montrer que l'ensemble ) est dense dans est dense dans ) . .
Et retrouver ensuite le résultat de l'exercice 30.
Bonne chance. je crois savoir ou vous voulez en venir  M-aI est inversible si et seulement si a n est pas une valeur propre de M M-(1/n)I est inversible pour tout n a partir d un certain rang et cette suite tend vers M retour a l exo 30 on definit B_{i,j,n} une suite de matrice inversible qui tend vers E_{i,j} les B_{i,j,n} sont libre grace a la liberte des E_{i,j} en passant a la limite d'ou le resultat | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 21:52 Lun 05 Aoû 2013, 21:52 | |
| - galillee56 a écrit:
- nmo a écrit:
- galillee56 a écrit:
- nmo a écrit:
- En attente d'une confirmation, je propose l'exercice suivant:
Exercice 30:
Montrer qu'il existe une base de ) constituée de matrices inversibles. constituée de matrices inversibles.
PS: L'exercice est tiré d'un Oral Banque Mine-Ponts (2013). en attendant une réponse a l'exo 29 je propose ceci pour l'exo 30
montrons que la famille (I+E_{i,j}) est libre supposons qu'elle liee c a dire qu il existe a_i,j tel sum(a_{i,j}(I+E_{i,j} (i,j) different de (i0,j0))=a_{i0,j0}(I+E_{i0+j0}) i0 differente de j0 en ecrivant la matrice a_(i0,j0)=0 il ne reste plus que les terme pour les quels i=j sum(a_{i,i}(I+E_{i,i}))=a_{i0,i0}(I+E_{i0,i0}) on trouve que les a_(i,i}=-a_{i0,i0} i different de i0 et la somme des a_{i,i} i different de i0 = 2a_{i0,i0} a_i0=0 donc ils sont tous nul la famille est libre bon cardinal c'est une base et tous les elements sont inversible L'idée est bonne. Mais ce n'est pas celle que j'attendais...
En attendant une confirmation de la solution précédente, je propose cet exercice:
Exercice 36:
Montrer que l'ensemble ) est dense dans est dense dans ) . .
Et retrouver ensuite le résultat de l'exercice 30.
Bonne chance. je crois savoir ou vous voulez en venir 
M-aI est inversible si et seulement si a n est pas une valeur propre de M
M-(1/n)I est inversible pour tout n a partir d un certain rang et cette suite tend vers M
retour a l exo 30 on definit B_{i,j,n} une suite de matrice inversible qui tend vers E_{i,j}
les B_{i,j,n} sont libre grace a la liberte des E_{i,j} en passant a la limite d'ou le resultat n est suppose fixe ici , parce quand tu dis on passe à la limite .. ? | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 22:06 Lun 05 Aoû 2013, 22:06 | |
| en fait le n c'est l entier qui verifie la liberte car on supposons que pour tout n B_{i,j,n} est liee en passant a la limite E_{i,j} aussi serait liee d'ou une contradiction
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 22:08 Lun 05 Aoû 2013, 22:08 | |
| - galillee56 a écrit:
- en fait le n c'est l entier qui verifie la liberte car on supposons que pour tout n B_{i,j,n} est liee en passant a la limite E_{i,j} aussi serait liee d'ou une contradiction
Ah d'accord, à toi de proposer un exercice | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 22:12 Lun 05 Aoû 2013, 22:12 | |
| bon voila un exo que je trouve vraiment marrant et tres interressant en meme temps c'est ULM
Exo 37:
soit N une matrice nilpotente de Mn(C) montrer que pour tout k dans N*, il existe N_{k} tq (I+N_{k}/k)^k=I+N et etudier la convergence de N_k et trouver la limite | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 22:28 Lun 05 Aoû 2013, 22:28 | |
| - Mehdi.O a écrit:
- nmo a écrit:
- galillee56 a écrit:
- bien joue mehdi.o
exo35:
 Je propose ma solution:
Il est très bien connu que les deux fonctions 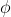 et et 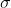 sont multiplicatives. sont multiplicatives.
Il suffit pour cela de comparer ces quantités lorsque  où où 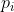 est premier et est premier et 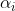 est un entier positif. est un entier positif.
On dispose des formules: =\sigma(p_i^{\alpha_i})=\frac{p_i^{\alpha_i+1}-1}{p_i-1}) et et =\phi(p_i^{\alpha_i})=(p_i-1)p_i^{\alpha_i-1}) . .
On a .\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}(p_i-1).p_i^{\alpha_i-1}<p_i^{2\alpha_i}=n^2) , ce qui dit que: , ce qui dit que: .\phi(n)}<n) . .
Et on a +\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}+(p_i-1).p_i^{\alpha_i-1}\ge2\sqrt{p_i^{\alpha_i-1}.(p_i^{\alpha_i+1}-1)}>2\sqrt{p_i^{2\alpha_i}}=2n) , donc , donc +\phi(n)}{2}>n) . .
On a donc pour  , les inégalités: , les inégalités: +\phi(n)}{2}>n>\sqrt{\sigma(n).\phi(n)}) . .
On retient les mêmes comparaisons pour n'importe quel entiers.
Sauf erreurs. Désolé mais prouver ça pour les puissances des premiers, ne nous permet pas de conclure pour tout entier pour l'inégalité où il y a la moyenne arithmétique. càd phi(n)+sigma(n)>=2n. Oui, tu as raison. En fait, j'ai voulu corriger. Mais, tu m'as devancé. - Mehdi.O a écrit:
- Sinon, voilà une preuve à cette inégalité dans le cas général :
On pose  ,l'inégalité à démontrer est : ,l'inégalité à démontrer est :
 , qui est équivalente à : , qui est équivalente à :

or les alpha_i sont tous supérieurs à 1, donc :
 . .
D'où le résultat. Je ne vois pas comment tu as aboutit à l'inégalité: +\prod_{i=1}^{r}(1-\frac{1}{p_i})\ge2) . Merci de détailler. | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Lun 05 Aoû 2013, 22:34 Lun 05 Aoû 2013, 22:34 | |
| - nmo a écrit:
- Mehdi.O a écrit:
- nmo a écrit:
- galillee56 a écrit:
- bien joue mehdi.o
exo35:
 Je propose ma solution:
Il est très bien connu que les deux fonctions 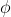 et et 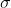 sont multiplicatives. sont multiplicatives.
Il suffit pour cela de comparer ces quantités lorsque  où où 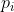 est premier et est premier et 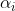 est un entier positif. est un entier positif.
On dispose des formules: =\sigma(p_i^{\alpha_i})=\frac{p_i^{\alpha_i+1}-1}{p_i-1}) et et =\phi(p_i^{\alpha_i})=(p_i-1)p_i^{\alpha_i-1}) . .
On a .\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}(p_i-1).p_i^{\alpha_i-1}<p_i^{2\alpha_i}=n^2) , ce qui dit que: , ce qui dit que: .\phi(n)}<n) . .
Et on a +\phi(n)=\frac{p_i^{\alpha_i+1}-1}{p_i-1}+(p_i-1).p_i^{\alpha_i-1}\ge2\sqrt{p_i^{\alpha_i-1}.(p_i^{\alpha_i+1}-1)}>2\sqrt{p_i^{2\alpha_i}}=2n) , donc , donc +\phi(n)}{2}>n) . .
On a donc pour  , les inégalités: , les inégalités: +\phi(n)}{2}>n>\sqrt{\sigma(n).\phi(n)}) . .
On retient les mêmes comparaisons pour n'importe quel entiers.
Sauf erreurs. Désolé mais prouver ça pour les puissances des premiers, ne nous permet pas de conclure pour tout entier pour l'inégalité où il y a la moyenne arithmétique. càd phi(n)+sigma(n)>=2n. Oui, tu as raison.
En fait, j'ai voulu corriger. Mais, tu m'as devancé.
- Mehdi.O a écrit:
- Sinon, voilà une preuve à cette inégalité dans le cas général :
On pose  ,l'inégalité à démontrer est : ,l'inégalité à démontrer est :
 , qui est équivalente à : , qui est équivalente à :

or les alpha_i sont tous supérieurs à 1, donc :
 . .
D'où le résultat. Je ne vois pas comment tu as aboutit à l'inégalité: +\prod_{i=1}^{r}(1-\frac{1}{p_i})\ge2) . .
Merci de détailler. Bah tu développes, on aura les mêmes termes à un signe près, ceux qui sont négatifs et positifs vont s'annuler et il restera 2 + des parcelles positives .. | |
|
  | |
Vz
Féru

 Nombre de messages : 63 Nombre de messages : 63
Age : 31
Date d'inscription : 14/11/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 06 Aoû 2013, 03:22 Mar 06 Aoû 2013, 03:22 | |
| | |
|
  | |
abdelbaki.attioui
Administrateur

 Nombre de messages : 2564 Nombre de messages : 2564
Localisation : maroc
Date d'inscription : 27/11/2005
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 06 Aoû 2013, 10:22 Mar 06 Aoû 2013, 10:22 | |
| | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mar 06 Aoû 2013, 16:22 Mar 06 Aoû 2013, 16:22 | |
| | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 07 Aoû 2013, 01:00 Mer 07 Aoû 2013, 01:00 | |
| Exo 38:
Montrer que pour qu'un endomorphisme de Mn(C) conserve le rang il suffit qu'il conserve le caractère inversible (C-à-d si A est inversible alors f(A) l'est aussi). | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 07 Aoû 2013, 01:48 Mer 07 Aoû 2013, 01:48 | |
| - expert_run a écrit:
- Exo 38:
Montrer que pour qu'un endomorphisme de Mn(C) conserve le rang il suffit qu'il conserve le caractère inversible (C-à-d si A est inversible alors f(A) l'est aussi). indice: - Spoiler:
soit A Mn(C) montrer qu'il existe P dans Gln(C) tq pour tout x dans R Ax+P est inversible et considerer le degre du polynome det(Ax+P) et montrer que f est inversible
| |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 07 Aoû 2013, 04:18 Mer 07 Aoû 2013, 04:18 | |
| Cet exercice est tiré d'un Ulm, mais avec des questions préliminaires, donc le donner directement c'est franchement très dur  , en tout cas j'ajoute une autre indication à celle de Galille56, essayer de montrer que f(M) est inversible ssi M inversible , et puis rg(f(M))>=rg(M)( pour démontrer cette inégalité, on montrera d'abord qu'il existe une matrice inversible G tq MG^-1 admette exactement rg(M) valeurs propres ) | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 07 Aoû 2013, 15:34 Mer 07 Aoû 2013, 15:34 | |
| moi ce que je trouve plutot interessant dans cet exo c'est de prouver que :
soit A dans Mn(C) il existe P tq pour tout x dans dans C Ax+P est inversible | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Mer 07 Aoû 2013, 18:02 Mer 07 Aoû 2013, 18:02 | |
| exo39:trouver la nature de la serie de terme general:  | |
|
  | |
expert_run
Expert sup

 Nombre de messages : 561 Nombre de messages : 561
Age : 30
Localisation : Marrakech
Date d'inscription : 30/01/2011
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 08 Aoû 2013, 04:23 Jeu 08 Aoû 2013, 04:23 | |
| - galillee56 a écrit:
- exo39:
trouver la nature de la serie de terme general:
 Solution:En posant (U_n)_n>=2 la suite en question et a=2pi*n. on a U_n =<int (2pi*n à (2n+1)pi) dt/(1+(a^2)sint)^(3/2) Or on a (1+(a^2 )sint )^(3/2)>=1+(a^3) (sint)^2 alors U_n<= int (2pi*n à (2n+1)pi) dt/(1+(a^3)sint)=2*int(0 à pi/2) dt/(1+(a^3)(sint)^2) En effectuant le changement de variable x=tan t on obtient: int(0 à pi/2) dt/(1+(a^3)sint)=int(0à+oo)dx/(1+x^2(1+a^3)) On pose encore u=xsqrt(1+a^3) alors int(0 à pi/2) dt/(1+(a^3)sint)=int(0à +00) du /((sqrt(1+a^3)(1+u^2))= pi/(2sqrt(1+a^3) qui est équivalent à pi/2a^(3/2) et puisque la série de terme général pi/2a^(3/2) converge alors la série en question converge. Dsl j'avais pas le temps de rédiger la solution en latex. | |
|
  | |
galillee56
Expert grade2

 Nombre de messages : 350 Nombre de messages : 350
Age : 29
Localisation : marrakech
Date d'inscription : 16/12/2012
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  Jeu 08 Aoû 2013, 04:42 Jeu 08 Aoû 2013, 04:42 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: direction mp mp* Sujet: Re: direction mp mp*  | |
| |
|
  | |
| | direction mp mp* |  |
|
