| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Lun 03 Fév 2014, 23:36 Lun 03 Fév 2014, 23:36 | |
| M. Ahmed TAHA a affirmé que : 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz dans le cas (a+b+c=3) .
J'essaierai de démontrer cette proposition qui est plus forte que celle qui stipule que: 3(xy+xz+yz)²+xyz(xy+xz+yz)>=10xyz .
Soient x,y,z>=0 et x+y+z=3.
On a 3(xy+yz+zx)^2 = (x+y+z)(xy+yz+zx)^2
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 5(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi xyz(xy+yz+zx) = x y^2 z^2 + y z^2 x^2 + z x^2 y^2
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
<--> 3(xy+yz+zx)^2 + xyz(xy+yz+zx) >= 30 (x^50 y^50 z^50)^(1/30) = 30(xyz)^(5/3) : IAG
Et comme 3 = x+y+z >= 3(xyz)^(1/3) : IAG <--> 1>= (xyz)^(1/3) <--> 1>= xyz, on a (xyz)^(5/3)>=xyz, donc 30(xyz)^(5/3) >= 30 xyz ,
donc 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz .
J'espère que cette démonstration est exempte d'erreurs, de plus je vous demande d'avoir l'amabilité de m'indiquer les étapes de la démonstration qui utilise le théorème du réordonnement: J'ai essayé de résoudre ce problème par cette méthode, mais je me suis trouvé inéxorablement face à un problème du sens de cette inéquation.
Merci d'avance. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 04 Fév 2014, 02:34 Mar 04 Fév 2014, 02:34 | |
| - aymanemaysae a écrit:
- M. Ahmed TAHA a affirmé que : 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz dans le cas (a+b+c=3) .
J'essaierai de démontrer cette proposition qui est plus forte que celle qui stipule que: 3(xy+xz+yz)²+xyz(xy+xz+yz)>=10xyz .
Soient x,y,z>=0 et x+y+z=3.
On a 3(xy+yz+zx)^2 = (x+y+z)(xy+yz+zx)^2
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 5(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi xyz(xy+yz+zx) = x y^2 z^2 + y z^2 x^2 + z x^2 y^2
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
<--> 3(xy+yz+zx)^2 + xyz(xy+yz+zx) >= 30 (x^50 y^50 z^50)^(1/30) = 30(xyz)^(5/3) : IAG
Et comme 3 = x+y+z >= 3(xyz)^(1/3) : IAG <--> 1>= (xyz)^(1/3) <--> 1>= xyz, on a (xyz)^(5/3)>=xyz, donc 30(xyz)^(5/3) >= 30 xyz ,
donc 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz .
J'espère que cette démonstration est exempte d'erreurs, de plus je vous demande d'avoir l'amabilité de m'indiquer les étapes de la démonstration qui utilise le théorème du réordonnement: J'ai essayé de résoudre ce problème par cette méthode, mais je me suis trouvé inéxorablement face à un problème du sens de cette inéquation.
Merci d'avance. dsl Mr aymanemaysae cette solution est fausse si 1 > xyz alors (xyz)^(5/3) <xyz | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 04 Fév 2014, 09:56 Mar 04 Fév 2014, 09:56 | |
| Rien ne sert de courir, il faut arriver à bon port.
A défaut de démontrer que: 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz, j'essaierai de démontrer que: 3(xy+xz+yz)²+xyz(xy+xz+yz)>=18xyz .
Et pour ne pas commettre la même erreur, je vais développer les deux côtés de l'inéquation et simplifier ensuite l'expression obtenue.
Soient x,y,z>=0 et x+y+z=3.
On a 3(xy+yz+zx)^2 = (x+y+z)(xy+yz+zx)^2
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 5(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi xyz(xy+yz+zx) = x y^2 z^2 + y z^2 x^2 + z x^2 y^2
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi 18 xyz = 2 * 9 * xyz = 2 (x+y+z)^2 xyz = 2 (x^2 + y^2 + z^2 + 2xy + 2yz + 2zx) xyz = 2 (x^3 yz + y^3 zx + z^3 xy + 2 x^2 y^2 z + 2 y^2 z^2 x + 2 z^2 x^2 y) ,
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)>= 18 xyz
<--> (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2) >= 2 (x^3 yz + y^3 zx + z^3 xy + 2 x^2 y^2 z + 2 y^2 z^2 x + 2 z^2 x^2 y)
<--> (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x y^2 z^2 + y z^2 x^2 + z x^2 y^2) >= 0 : expression logiquement vraie car x,y et z sont des réels positifs.
donc 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 18 xyz.
Ceci implique que 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 10 xyz (CQFD).
J'ose espèrer que cette démonstration est exempte d'erreurs, de plus je vous demande d'avoir l'amabilité de m'indiquer les étapes de la démonstration qui utilise le théorème du réordonnement: J'ai essayé de résoudre ce problème par cette méthode, mais je me suis trouvé inéxorablement face à un problème du sens de cette inéquation.
Merci d'avance. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 04 Fév 2014, 10:31 Mar 04 Fév 2014, 10:31 | |
| - aymanemaysae a écrit:
- Rien ne sert de courir, il faut arriver à bon port.
A défaut de démontrer que: 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 30xyz, j'essaierai de démontrer que: 3(xy+xz+yz)²+xyz(xy+xz+yz)>=18xyz .
Et pour ne pas commettre la même erreur, je vais développer les deux côtés de l'inéquation et simplifier ensuite l'expression obtenue.
Soient x,y,z>=0 et x+y+z=3.
On a 3(xy+yz+zx)^2 = (x+y+z)(xy+yz+zx)^2
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 5(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi xyz(xy+yz+zx) = x y^2 z^2 + y z^2 x^2 + z x^2 y^2
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)
= (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2)
On a aussi 18 xyz = 2 * 9 * xyz = 2 (x+y+z)^2 xyz = 2 (x^2 + y^2 + z^2 + 2xy + 2yz + 2zx) xyz = 2 (x^3 yz + y^3 zx + z^3 xy + 2 x^2 y^2 z + 2 y^2 z^2 x + 2 z^2 x^2 y) ,
donc 3(xy+yz+zx)^2 + xyz(xy+yz+zx)>= 18 xyz
<--> (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x^3 yz + y^3 zx + z^3 xy) + 6(x y^2 z^2 + y z^2 x^2 + z x^2 y^2) >= 2 (x^3 yz + y^3 zx + z^3 xy + 2 x^2 y^2 z + 2 y^2 z^2 x + 2 z^2 x^2 y)
<--> (x^3 y^2 + y^3 z^2 + z^3 x^2) + (x^2 y^3 + y^2 z^3 + z^2 x^3) + 2(x y^2 z^2 + y z^2 x^2 + z x^2 y^2) >= 0 : expression logiquement vraie car x,y et z sont des réels positifs.
donc 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 18 xyz.
Ceci implique que 3(xy+xz+yz)²+xyz(xy+xz+yz) >= 10 xyz (CQFD).
J'ose espèrer que cette démonstration est exempte d'erreurs, de plus je vous demande d'avoir l'amabilité de m'indiquer les étapes de la démonstration qui utilise le théorème du réordonnement: J'ai essayé de résoudre ce problème par cette méthode, mais je me suis trouvé inéxorablement face à un problème du sens de cette inéquation.
Merci d'avance. bah voici une méthode plus simple on a 3(xy+xz+yz)² > 9xyz(x+y+z)=27xyz alors 3(xy+xz+yz)²+xyz(xy+xz+yz) > 27xyz c tt | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 04 Fév 2014, 13:13 Mar 04 Fév 2014, 13:13 | |
| Cette méthode est si élégante que je ne peux me priver de lui rendre les honneurs qui lui sont dus en la réécrivant en détail:
Soient x,y et z des réels positifs tels que x+y+z = 3,
on a (xy + yz + zx)^2 = x^2 y^2 + y^2 z^2 + z^2 x^2 + 2 xy z^2 + 2 yz x^2 + 2 zx y^2,
et comme x^2 y^2 + y^2 z^2 + z^2 x^2 >= xy z^2 + yz x^2 + zx y^2: application de la formule a^2 +b^2 +c^2 >= ab+bc+ca avec a = xy, b = yz et c = zx ,
on a:
(xy + yz + zx)^2 >= 3 (xy z^2 + yz x^2 + zx y^2) = 3 xyz (x+y+z) = 9 xyz,
donc 3 (xy + yz + zx)^2 >= 27 xyz
et par conséquent: 3 (xy + yz + zx)^2 + xyz(xy + yz + zx) >= 27 xyz.
Vraiment c'est ingénieux, Bravo! | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 07 Fév 2014, 16:14 Ven 07 Fév 2014, 16:14 | |
| voici une autre
Soit x,y et z des réels positifs tel que : x+y+z=3
Montrer que : 3(xy+xz+yz)²+xyz(xy+xz+yz)>10xyz
et que : 9(xy+xz+yz)+4xyz(xy+xz+yz)>4(xy+xz+yz)²+3xyz
Pour la deuxième inéquation, je n'ai pas trouvé de solution. Si M. Taha a l'obligeance de m'indiquer un chemin pour le résoudre, je lui serai très reconnaissant: j'ai tout essayé, et je crois qu'il y a une astuce que j'aimerai connaître.
Merci | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 11 Fév 2014, 20:18 Mar 11 Fév 2014, 20:18 | |
| Bonsoir; j'ajoute une autre inegalité :
a,b et c etant des reels positifs t.q : a+b+c=1
Trouvez la valeur maximale de l expression
1/(a^2-4a+9) + 1/(b^2-4b+9) + 1/(c^2-4c+9) .
Bonne chance !
AMICALEMENT. | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 11 Fév 2014, 23:46 Mar 11 Fév 2014, 23:46 | |
| M. Humber dans cette page: https://mathsmaroc.jeun.fr/t20477-aide-sur-une-olympiade#171054 avait donné une démonstration très élégante de cet exercice dont le résultat est : 7/18. M. Humber avait écrit: Bonsoir à tous les matheux,Jensen ne marche pas pour cet exercice, essayez de majorer chacun des trois termes par une fonction f . La somme contiendra le a+b+c qui vaut 1 et le 7 /18 . Il faut donc penser à retrancher 1 à 7 et diviser ce qui reste par 3 pour se rapprocher de la majoration. Il faut remarquer sinon que cette fonction majorante égale l'un des termes de l'inégalité pour 0 et 1. Donc si f(x)=ax+b : 1/9=b et a+b=1/(1-4+9)=1/6 ce qui donne b=1/9 et a=1/18. Conclusion : f(x)=(x+2)/18 . Il ne reste plus qu'à vérifier qu'elle satisfait bien la majoration voulue.Merci pour vous deux: c'était très constructif. | |
|
  | |
bianco verde
Maître

 Nombre de messages : 208 Nombre de messages : 208
Age : 26
Localisation : la terre
Date d'inscription : 19/12/2013
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 12 Fév 2014, 12:28 Mer 12 Fév 2014, 12:28 | |
| j'ajoute une autre : x y et z des reels positifs tels que 1/x + 1/y + 1/z= 2 montrez que V(x+y+z)>=SumV(x-1) {iran 1998}
Mr.aymanemaysae ^^ merci pour vos interventions «» ce sujet est trop bon pour l'achever maintenant . | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 12 Fév 2014, 16:49 Mer 12 Fév 2014, 16:49 | |
| - aymanemaysae a écrit:
- voici une autre
Soit x,y et z des réels positifs tel que : x+y+z=3
Montrer que : 3(xy+xz+yz)²+xyz(xy+xz+yz)>10xyz
et que : 9(xy+xz+yz)+4xyz(xy+xz+yz)>4(xy+xz+yz)²+3xyz
Pour la deuxième inéquation, je n'ai pas trouvé de solution. Si M. Taha a l'obligeance de m'indiquer un chemin pour le résoudre, je lui serai très reconnaissant: j'ai tout essayé, et je crois qu'il y a une astuce que j'aimerai connaître.
Merci dsl Mr aymanemaysae mai Je n'ai pas encore trouvé une solution complète. | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 12 Fév 2014, 17:17 Mer 12 Fév 2014, 17:17 | |
| - bianco verde a écrit:
- j'ajoute une autre : x y et z des reels positifs tels que 1/x + 1/y + 1/z= 2 montrez que V(x+y+z)>=SumV(x-1) {iran 1998}
Mr.aymanemaysae ^^ merci pour vos interventions «» ce sujet est trop bon pour l'achever maintenant . voici a solution  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 12 Fév 2014, 17:22 Mer 12 Fév 2014, 17:22 | |
| | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 | |
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 | |
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 18 Fév 2014, 12:36 Mar 18 Fév 2014, 12:36 | |
| Merci M. Ahmed_TAHA, grâce à votre indice j'ai pu orienter mes recherches et trouver une page dans un livre qui explicite trois solutions de cet exercice: vos remarques et vos indices me sont toujours d'un grand secours dans ma quête du savoir. Pour ne rien vous cacher, ça faisait presque plus de dix jours que je cherchais inlassablement une solution à cet exercice qui revenait à mon esprit comme un leitmotiv, et ce n'est que votre indice qui m'a mis sur le bon chemin à suivre: encore une fois Merci.  | |
|
  | |
Ahmed Taha
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 28
Localisation : lmarriikh
Date d'inscription : 06/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 18 Fév 2014, 15:11 Mar 18 Fév 2014, 15:11 | |
| - aymanemaysae a écrit:
- Merci M. Ahmed_TAHA, grâce à votre indice j'ai pu orienter mes recherches et trouver une page dans un livre qui explicite trois solutions de cet exercice: vos remarques et vos indices me sont toujours d'un grand secours dans ma quête du savoir.
Pour ne rien vous cacher, ça faisait presque plus de dix jours que je cherchais inlassablement une solution à cet exercice qui revenait à mon esprit comme un leitmotiv, et ce n'est que votre indice qui m'a mis sur le bon chemin à suivre: encore une fois Merci.
 pour la 1er solution on a l'inverse par chebychev 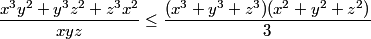 donc la 1er solution est fausse. pour la 3eme ca sera facile par la méthode de Mr legend-crush ou par Caushy on a  donc 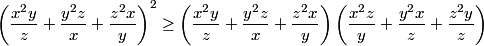 et par Caushy 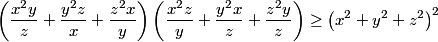 alors 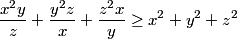 en tt cas merci pour les solutions  . | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 18 Fév 2014, 17:17 Mar 18 Fév 2014, 17:17 | |
| Pour montrer l'indice que Mr Ahmad Taha a donné, c'est equivalent à:
x(y²-z²)+yz(y-z)>=0 (x>y>z>0) ce qui complete la solution je pense | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 18 Fév 2014, 22:14 Mar 18 Fév 2014, 22:14 | |
| salut. je propose un exercice si ca genes pas trop ^^ 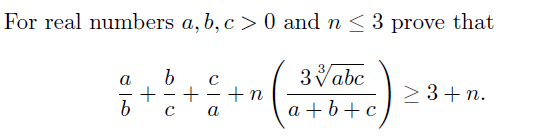 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 19 Fév 2014, 00:04 Mer 19 Fév 2014, 00:04 | |
| M. Ahmed Taha, vous avez raison en ce qui concerne la solution n° 1 de l'exercice: votre remarque m'a évité d'induire dans l'erreur les visiteurs de cette page et aussi de me rendre compte que certaines éditions sur le Web ne sont pas fiables, je ne peux que vous en remercier. De plus, la solution que vous avez proposée est de loin la meilleure.
M. legend-Crush, j'ai essayé de retrouver l'équivalence que vous avez obtenu, mais en vain. j'espère que vous aurez l'amabilité de me l'expliciter: ce sera vraiment très gentil de votre part et très constructif pour moi. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 19 Fév 2014, 00:29 Mer 19 Fév 2014, 00:29 | |
| - aymanemaysae a écrit:
M. legend-Crush, j'ai essayé de retrouver l'équivalence que vous avez obtenu, mais en vain. j'espère que vous aurez l'amabilité de me l'expliciter: ce sera vraiment très gentil de votre part et très constructif pour moi. Pour etre franc c'est dans un livre que je l'ai trouvé, mmais voici les étapes: c'est equivalent à: 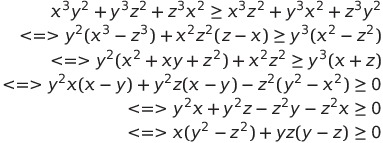 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 19 Fév 2014, 15:14 Mer 19 Fév 2014, 15:14 | |
| Merci M.Legend_Crush d'avoir répondu à ma demande malgré qu'il faisait très tard. En ce qui concerne votre méthode, permettez-moi d'exprimer quelques remarques qui n'occultent guère sa splendeur: 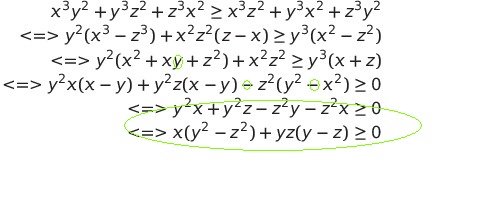 - Dans la troisième ligne il y a une faute de frappe: un "y" à la place d'un "z". - Dans la quatrième ligne, deux autres fautes de frappe qui vous ont empêché de conclure: les deux "-" à la place des deux "+" vous ont forcé à ajouter les deux dernières lignes, alors qu'il suffisait de conclure par y^2 x(x-y) + y^2 z (x-y) + z^2 (y^2 + x^2) >= 0 : expression logiquement vraie, puisque x>=y. A la fin, je vous félicite pour l'idée principale de la démonstration qui consistait à mettre en facteur (x-y), chose à laquelle je n y pas pensé. | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 19 Fév 2014, 17:35 Mer 19 Fév 2014, 17:35 | |
| - aymanemaysae a écrit:
- Merci M.Legend_Crush d'avoir répondu à ma demande malgré qu'il faisait très tard.
En ce qui concerne votre méthode, permettez-moi d'exprimer quelques remarques qui n'occultent guère sa splendeur:
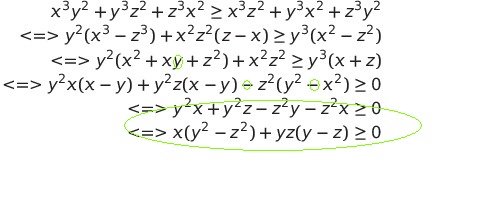
- Dans la troisième ligne il y a une faute de frappe: un "y" à la place d'un "z".
- Dans la quatrième ligne, deux autres fautes de frappe qui vous ont empêché de conclure:
les deux "-" à la place des deux "+" vous ont forcé à ajouter les deux dernières lignes, alors qu'il suffisait de conclure
par y^2 x(x-y) + y^2 z (x-y) + z^2 (y^2 + x^2) >= 0 : expression logiquement vraie, puisque x>=y.
A la fin, je vous félicite pour l'idée principale de la démonstration qui consistait à mettre en facteur
(x-y), chose à laquelle je n y pas pensé. Desolé pour les fautes de frappe, C'était à coup sûr a cause de l'heure, et le fait que j'utilisais un ordinateur avec bq de touches manquantes . Sinon, Je propose une inegalité: Let a,b,c,d be REAL numbers such that a²+b²+c²+d²=4. Prove that a^3+b^3+c^3+d^3 =< 8 | |
|
  | |
aymanemaysae
Expert grade1
 Nombre de messages : 428 Nombre de messages : 428
Age : 28
Date d'inscription : 22/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 19 Fév 2014, 21:00 Mer 19 Fév 2014, 21:00 | |
| Merci pour l'inéquation: je préfère la désignation d' "inéquation" à celle d' "inégalité". En ce qui concerne la résolution de l'exercice, j'avoue que pendant sa rédaction, j'avais le sentiment du "Déjà vu", ou plus précisément du "Déjà résolu". En tout cas voici ma proposition:  Si ma démonstration est exempte d'erreurs, je ne propose aucun exercice pour laisser l'occasion à l'exercice de M. Elidrissi que je trouve très intéressant: 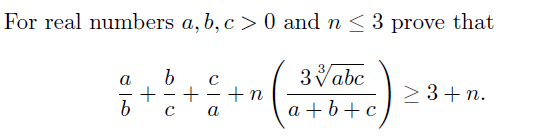 | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 21 Fév 2014, 21:20 Ven 21 Fév 2014, 21:20 | |
| On pose :  Sauf erreur de ma part, l'inégalité est équivalente à :  Où :   On utilise la méthode SOS-Schur en supposant que  est le plus petit élément et il nous suffit de démontrer que les expressions  et  sont positives, ce qui je pense être vrai sans vouloir me noyer dans les calculs. | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 21 Fév 2014, 23:15 Ven 21 Fév 2014, 23:15 | |
| | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
