| | monde des inégalités |  |
|
+16King elidrissi Nas8 Amine Natik aymanemaysae DAMP aymas Ahmed Taha nmo bianco verde Zouhair-Evariste Humber seledeur legend-crush Sketshup L-W-P 20 participants |
|
| Auteur | Message |
|---|
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 21 Fév 2014, 23:27 Ven 21 Fév 2014, 23:27 | |
| | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Ven 21 Fév 2014, 23:56 Ven 21 Fév 2014, 23:56 | |
| J'ai pas comprit comment l'utilisé mais en tout cas merci voici la solution :  En tout cas c'est mon frère qui m'a aidé à trouver la solution  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 00:03 Sam 22 Fév 2014, 00:03 | |
| vraiment tres bien!!
, mais une petite correction, c est xyz=1 pas abc=1
et ca c est pour n=3.il reste n=2 et n=1
je crois que c est a toi de poster un exercice | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 00:21 Sam 22 Fév 2014, 00:21 | |
| - elidrissi a écrit:
- vraiment tres bien!!
, mais une petite correction, c est xyz=1 pas abc=1
et ca c est pour n=3.il reste n=2 et n=1
je crois que c est a toi de poster un exercice oui vous avez raison xyz=1 dans le cas n=3 l'inégalité est plus forte alors les deux autres cas n£{1,2} sont facile. voici l'inégalité que j'ai trouvé  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 02:12 Sam 22 Fév 2014, 02:12 | |
| on a selon le theoreme de T2 : 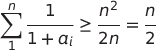 AM-GM:  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 09:01 Sam 22 Fév 2014, 09:01 | |
| si c'est correct, je laisse place a Mr.aymanemaysae qui a eu l’amabilité de me laisser son tour | |
|
  | |
Freud.
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Localisation : Casablanca
Date d'inscription : 22/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 11:42 Sam 22 Fév 2014, 11:42 | |
| voici un autre exo que je n'arrive pas à résourdre  Prove that in any acute-angled triangle ABC we have :  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 20:12 Sam 22 Fév 2014, 20:12 | |
| LHS = 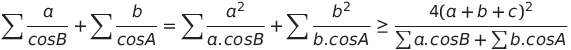 on a  ce qui est vrai. on a donc l inegalitee demandee. sauf erreur  | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 | |
  | |
Freud.
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Localisation : Casablanca
Date d'inscription : 22/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 21:00 Sam 22 Fév 2014, 21:00 | |
| bravo, trés bon solution à toi mnt poste un exo  | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 21:01 Sam 22 Fév 2014, 21:01 | |
| merci ^^
come j ai dis plutot je laisse mon tour a Mr. Aymanemaysae, comme il a eu l amabilitee de me passer le sien | |
|
  | |
Freud.
Débutant

 Nombre de messages : 10 Nombre de messages : 10
Age : 27
Localisation : Casablanca
Date d'inscription : 22/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 21:09 Sam 22 Fév 2014, 21:09 | |
| autre solution proposé (c'est pas ma solu) : Notre ing devient   par Cauchez :   donc on peut slmn démonter  fini  | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Sam 22 Fév 2014, 22:52 Sam 22 Fév 2014, 22:52 | |
| | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 11:18 Dim 23 Fév 2014, 11:18 | |
| d'accord, merci Mr.
je dois reviser ma trigo apparement | |
|
  | |
King
Maître

 Nombre de messages : 125 Nombre de messages : 125
Age : 32
Localisation : The Castle
Date d'inscription : 03/08/2010
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 19:02 Dim 23 Fév 2014, 19:02 | |
| Vous trouverez ici un document que j'avais rédigé il y a plus de 3 ans, et qui comporte une grande partie des identités et des inégalités à connaître pour résoudre les inégalités géométriques.
http://www.mediafire.com/view/2yydvylxhe881p3/Geo-Triangle.pdf
NB : J'avais oublié de signaler sur le document que l'inégalité de Walker n'est applicable que dans un triangle aigu, d'ailleurs ça se voit à partir de la démonstration. | |
|
  | |
elidrissi
Maître

 Nombre de messages : 258 Nombre de messages : 258
Age : 27
Localisation : maths land
Date d'inscription : 03/06/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 20:10 Dim 23 Fév 2014, 20:10 | |
| tres bien fait Mr. je tacherais de tout apprendre. il ne manque qu un peu d exercices pour assimiler , a mon avis. apres tout, on continue le marathon. voila un bon exo : 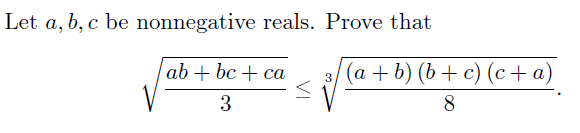 | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 | |
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 21:23 Dim 23 Fév 2014, 21:23 | |
| soient x,y,z des réels positifs vérifiant la relation x+y+z=1.
Démontrer la double inégalité : 0<xy+xz+yz-2xyz<7/27 | |
|
  | |
legend-crush
Expert sup

 Nombre de messages : 545 Nombre de messages : 545
Age : 27
Localisation : Rabat
Date d'inscription : 25/12/2012
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 21:37 Dim 23 Fév 2014, 21:37 | |
| La première partie peut être prouvée comme suit:
(x+y+z)(1/x+1/y+1/z)>=9 ==> xy+xz+yz>=9xyz ==> xy+xz+yz-2xyz>=7xyz >=0
Sauf Erreur | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Dim 23 Fév 2014, 23:36 Dim 23 Fév 2014, 23:36 | |
| - legend-crush a écrit:
- La première partie peut être prouvée comme suit:
(x+y+z)(1/x+1/y+1/z)>=9 ==> xy+xz+yz>=9xyz ==> xy+xz+yz-2xyz>=7xyz >=0
Sauf Erreur cette solution est vrai quand x,y,z>0 donc il faut étudie les deux cas z=0 et x,y>0 ou y=z=0 et x=1 ou bien il suffit de remplacer 1/x+1/y+1/z par xy+xz+yz. | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mar 25 Fév 2014, 16:52 Mar 25 Fév 2014, 16:52 | |
| - elmrini a écrit:
- soient x,y,z des réels positifs vérifiant la relation x+y+z=1.
Démontrer la double inégalité : 0<xy+xz+yz-2xyz<7/27 pour continuer je poste une solution pour ce problème d'aprés Schur  d'où : xy+xz+yz-2xyz <7/27 Que chacun se sente libre de proposer une nouvelle inégalité. | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 26 Fév 2014, 15:34 Mer 26 Fév 2014, 15:34 | |
| a,b,c réels positifs Montrez que 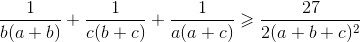 | |
|
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 | |
  | |
elmrini
Maître
 Nombre de messages : 80 Nombre de messages : 80
Age : 28
Date d'inscription : 21/02/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 26 Fév 2014, 16:17 Mer 26 Fév 2014, 16:17 | |
| si vous avez une autre tu peu le proposer  | |
|
  | |
DAMP
Féru
 Nombre de messages : 45 Nombre de messages : 45
Age : 28
Date d'inscription : 08/01/2014
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  Mer 26 Fév 2014, 16:40 Mer 26 Fév 2014, 16:40 | |
| Bien joué il y un une autre méthode avec Hölder: On a: 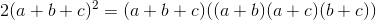 L’inégalité est donc équivalente a 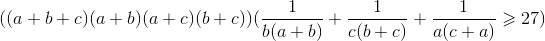 Ce qui est vrais avec l’inégalité de Hölder. A toi de poster | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: monde des inégalités Sujet: Re: monde des inégalités  | |
| |
|
  | |
| | monde des inégalités |  |
|
