| | #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> |  |
|
+27schwartz Newton abdelilah o0aminbe0o kaderov saad007 Weierstrass stipuler yassine-mansouri badr ali 20/20 khamaths Oumzil otman4u rockabdel selfrespect samir JASPER Conan the lord of the maths radouane_BNE stof065 codex00 saiif3301 wiles digital_brain Alaoui.Omar 31 participants |
|
| Auteur | Message |
|---|
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 20:51 Dim 01 Juil 2007, 20:51 | |
| pardon Mr Samir , car je ne l'avais pas vu , mais la solution qu'a donné
Mr abdelbaki est surprenante ! | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 20:55 Dim 01 Juil 2007, 20:55 | |
| EXERCICE N°20
soit : a,b,c >= 0
Montrer Que : a^4b + b^4c + c^4d + d^4a >= abcd(a+b+c+d)
Lisez ce qui est en rouge avant de répondre
Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 21:00 Dim 01 Juil 2007, 21:00 | |
| salut
par symetrie des rôle on peut supposé que a>=b>=c>=d .d'aprés chebychev et aussi AM_GM on a
a^4b + b^4c + c^4d + d^4a >= 1/4(a^4 + b^4 + c^4 + d^4)(a+b+c+d) >=1/4 (a+b+c+d)(4*abcd^(4/4) )=abcd(a+b+c+d)
__BestFriend__
Dernière édition par le Dim 01 Juil 2007, 22:07, édité 1 fois | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 21:11 Dim 01 Juil 2007, 21:11 | |
| allez BestFriend propose un autre exo | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 21:38 Dim 01 Juil 2007, 21:38 | |
| - BeStFrIeNd a écrit:
- salut
par symetrie des rôle on peut supposé que a>=b>=c>=d .d'aprés chebychev et aussi AM_GM on a
a^4b + b^4c + c^4d + d^4a >= 1/4(a^4 + b^4 + c^4 + d^4)(a+b+c+d) >=1/4 (a+b+c+d)(4*abcd^(1/4) )=abcd(a+b+c+d)
__BestFriend__ me ne dis pas seulement les theoremes , explique !surtout celle de chebychev  | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:09 Dim 01 Juil 2007, 22:09 | |
| comment ça
a^4b + b^4c + c^4d + d^4a >= 1/4(a^4 + b^4 + c^4 + d^4)(a+b+c+d) | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:16 Dim 01 Juil 2007, 22:16 | |
| - Conan a écrit:
- comment ça
a^4b + b^4c + c^4d + d^4a >= 1/4(a^4 + b^4 + c^4 + d^4)(a+b+c+d) D'abord je comprend pas où est ton probléme! par symétrie des rôle ,on peut supposer que: a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4 Donc a^4b + b^4c + c^4d + d^4a >=(1/4)( a^4 + b^4 + c^4 + d^4 )(a+b+c+d)c'est tout! | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:18 Dim 01 Juil 2007, 22:18 | |
| mais comment tu as passer de ça
a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4
à ça :
a^4b + b^4c + c^4d + d^4a >=(1/4)(a^4 + b^4 + c^4 + d^4)(a+b+c+d) | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:20 Dim 01 Juil 2007, 22:20 | |
| - Conan a écrit:
- mais comment tu as passer de ça
a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4
à ça :
a^4b + b^4c + c^4d + d^4a >=(1/4)(a^4 + b^4 + c^4 + d^4)(a+b+c+d) Tu peut demander a chebychev mon ami. | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:23 Dim 01 Juil 2007, 22:23 | |
| - BeStFrIeNd a écrit:
- Conan a écrit:
- mais comment tu as passer de ça
a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4
à ça :
a^4b + b^4c + c^4d + d^4a >=(1/4)(a^4 + b^4 + c^4 + d^4)(a+b+c+d)
Tu peut demander a chebychev mon ami. mais fais attention : on a a^4b + b^4c + c^4d + d^4a mais pour que ça soit avec chebychev , on dois avoir : a^4d + b^4c + c^4b + d^4a | |
|
  | |
Oumzil
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 28/08/2006
 |  Sujet: salut Sujet: salut  Dim 01 Juil 2007, 22:23 Dim 01 Juil 2007, 22:23 | |
| voilà une sollution : ( c'est la même qu'a bestfreind )  PS: on peut supposer que a >= b >= c >= d | |
|
  | |
digital_brain
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 31/03/2007
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:25 Dim 01 Juil 2007, 22:25 | |
| - Conan a écrit:
- mais comment tu as passer de ça
a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4
à ça :
a^4b + b^4c + c^4d + d^4a >=(1/4)(a^4 + b^4 + c^4 + d^4)(a+b+c+d) ce passage la conan est exactement l inegalite de chybechev | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:29 Dim 01 Juil 2007, 22:29 | |
| - digital_brain a écrit:
- Conan a écrit:
- mais comment tu as passer de ça
a >= b >= c >= d <==> a^4 >= b^4 >= c^4 >= d^4
à ça :
a^4b + b^4c + c^4d + d^4a >=(1/4)(a^4 + b^4 + c^4 + d^4)(a+b+c+d)
ce passage la conan est exactement l inegalite de chybechev on a a^4b + b^4c + c^4d + d^4a mais pour que ça soit avec chebychev , on dois avoir :a^4d + b^4c + c^4b + d^4a | |
|
  | |
Oumzil
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 28/08/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:35 Dim 01 Juil 2007, 22:35 | |
| Conan ton exercice est numero 1 ou 2 ( en rouge ) ? 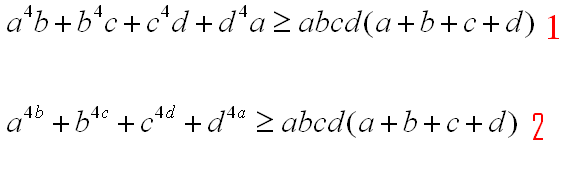 | |
|
  | |
saiif3301
Expert grade2
 Nombre de messages : 378 Nombre de messages : 378
Age : 34
Localisation : benslimane
Date d'inscription : 07/05/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:35 Dim 01 Juil 2007, 22:35 | |
| oui ta raison pour chebechève c est pas n importe quoi il faut avoir le plus grand avec le plus grand pour faire chèbèchve | |
|
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:36 Dim 01 Juil 2007, 22:36 | |
| - Oumzil a écrit:
- Conan ton exercice est numero 1 ou 2 ( en rouge ) ?
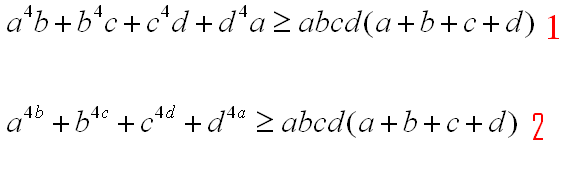 num 1 | |
|
  | |
saiif3301
Expert grade2
 Nombre de messages : 378 Nombre de messages : 378
Age : 34
Localisation : benslimane
Date d'inscription : 07/05/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:39 Dim 01 Juil 2007, 22:39 | |
| mais att on doit voir si la rèponce de bestfriend est juste ou nn | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 | |
  | |
Conan
Expert sup

 Nombre de messages : 1722 Nombre de messages : 1722
Age : 34
Localisation : Paris
Date d'inscription : 27/12/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 22:42 Dim 01 Juil 2007, 22:42 | |
| - saiif3301 a écrit:
- mais att on doit voir si la rèponce de bestfriend est juste ou nn
ce n'etais pas le theo de chebychev mais celui de réordonnement  regarde page 11 coté inegalité | |
|
  | |
Oumzil
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 28/08/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 23:35 Dim 01 Juil 2007, 23:35 | |
| voilà la sollution que je proposes :  | |
|
  | |
stof065
Expert sup

 Nombre de messages : 540 Nombre de messages : 540
Age : 34
Date d'inscription : 01/02/2007
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 23:38 Dim 01 Juil 2007, 23:38 | |
| qlq soit n£N n=2k ou n=2k+1
pour n=2k
(3^n-2^n)/n = (9^k-4^k)/2k
=(5*sum(de i=0 a k-1) 9^k-i-1*4^i)/2k
=(5*(4Q+9^n))/2k ( n est pas un entier)
n=2k+1
(3^n-2^n)/n= (3*9^k-2*4^k)/(2k+1)
=(3(9^k-4^k)+4^k)/(2k+1)
=(3(9^k-4^k))/(2k+1) + (4^k)/(2k+1)
n>=2
PGCD(4.(2k+1))=1
<=>PGCD(4^n.(2k+1))=1
c-à-d 4^n/(2k+1) n appartien pas a N | |
|
  | |
Oumzil
Maître

 Nombre de messages : 240 Nombre de messages : 240
Age : 35
Date d'inscription : 28/08/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Dim 01 Juil 2007, 23:50 Dim 01 Juil 2007, 23:50 | |
| - stof065 a écrit:
- n=2k+1
(3^n-2^n)/n= (3*9^k-2*4^k)/(2k+1)
=(3(9^k-4^k)+4^k)/(2k+1)
=(3(9^k-4^k))/(2k+1) + (4^k)/(2k+1)
n>=2
PGCD(4.(2k+1))=1
<=>PGCD(4^n.(2k+1))=1
c-à-d 4^n/(2k+1) n appartien pas a N Je crois qu'il faut prouver que (3(9^k-4^k))/(2k+1) appartient à IN  car la somme de deux nombre qui sont pas entiers peut etre entière  | |
|
  | |
Alaoui.Omar
Expert sup

 Nombre de messages : 1738 Nombre de messages : 1738
Age : 34
Localisation : London
Date d'inscription : 29/09/2006
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Lun 02 Juil 2007, 02:11 Lun 02 Juil 2007, 02:11 | |
| - stof065 a écrit:
- qlq soit n£N n=2k ou n=2k+1
pour n=2k
(3^n-2^n)/n = (9^k-4^k)/2k
=(5*sum(de i=0 a k-1) 9^k-i-1*4^i)/2k
=(5*(4Q+9^n))/2k ( n est pas un entier)
n=2k+1
(3^n-2^n)/n= (3*9^k-2*4^k)/(2k+1)
=(3(9^k-4^k)+4^k)/(2k+1)
=(3(9^k-4^k))/(2k+1) + (4^k)/(2k+1)
n>=2
PGCD(4.(2k+1))=1
<=>PGCD(4^n.(2k+1))=1
c-à-d 4^n/(2k+1) n appartien pas a N utilise le mathstype stp | |
|
  | |
ali 20/20
Maître

 Nombre de messages : 239 Nombre de messages : 239
Date d'inscription : 01/07/2007
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Lun 02 Juil 2007, 12:05 Lun 02 Juil 2007, 12:05 | |
| est c que je peus participer dans votre tournoi | |
|
  | |
samir
Administrateur

Nombre de messages : 1872
Localisation : www.mathematiciens.tk
Date d'inscription : 23/08/2005
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  Lun 02 Juil 2007, 12:21 Lun 02 Juil 2007, 12:21 | |
| - ali 20/20 a écrit:
- est c que je peus participer dans votre tournoi
non vous n'estes pas parmis les inscrits | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> Sujet: Re: #Grand Jeu d'été (2007 ) TSM EST COMENCE ==>  | |
| |
|
  | |
| | #Grand Jeu d'été (2007 ) TSM EST COMENCE ==> |  |
|
