#Grand Jeu d'été (2007 ) TSM EST COMENCE ==>

et voila que je me reppel c'est un exo du premier test des olympiades de premiere

Ton exo Conan!!

où est l'exo Conan,

x,y,z >=0 ,tel que : xyz >= 1

montrer que :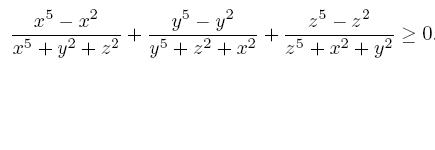

#Grand Jeu d'été (2007 ) TSM EST COMENCE ==> - Page 13 070710064505836656

Expert sup Nombre de messages : 540 Age : 34 Date d'inscription : 01/02/2007

deja postée

et ancien exo de l'oim

EXRCICE N° 28
montrer que pour tout a,b,c >0 tel que abc = 1

#Grand Jeu d'été (2007 ) TSM EST COMENCE ==> - Page 13 07071010

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

piusque a,betc sont strictement positifs et abc=1 alors on a au moins deux nombres,par exemple b-1 et c-1, qui vérifient (b-1)(c-1)>=0(ce cas est toujours vérifié).
d'après Holder on a:
(a^3+1)(b^3+1)(c^3+1)>=(a+bc)^3
<=>rac3((a^3+1)(b^3+1)(c^3+1))+1>=a+bc+1
il suffit alors de montrer que:
a+bc+1>=1/a+1/b+1/c=ab+bc+ca
<=>a+1>=ab+ac
<=>a(1-b)+ac(b-1)>=0
<=>(b-1)(c-1)>=0
ce qui est vrai d'après la première remarque.
d'où le réponse.
j'ai une belle solution que je vais poster après.

salut boukharfane ! je l'ai troué assez artificiel! holder:!!!!!! ya pas de methodes directe?

comme j'ai mentionné,il ya une autre méthode belle et directe comme tu veux mais ça demande bcp de temps pour l'écrire,et je te promets que je vais la poster as soon as possible.

EXERCICE N° 29
Soient x,y,a et b des réels positifs tels que x#y;x#2y,y#2x,a#3b et
(2x-y)/(2y-x)=(a+3b)/(a-3b)
PROUVER que (x²+y²)/(x²-y²)>=1

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

c'est evident non? y² sup -y²

boukharfane radouane a écrit:: salut tout le monde!
Soient x,y,a et b des réels positifs tels que x#y;x#2y,y#2x,a#3b et
(2x-y)/(2y-x)=(a+3b)/(a-3b).
PROUVER que (x²+y²)/(x²-y²)>=1

pour l'exo de Conan,je vous propose une autre méthode!
le truc de cet exericie réside dans la substitution suivante:
Posons p=a+b+c et q=ab+bc+ca.
On a (a^3+1)(b^3+1)(c^3+1)=(abc)^3+1+a^3+b^3+c^3+(ab)^3+(bc)^3+(ca)^3
d'autre part:
a^3+b^3+c^3=p^3-3pq+3 et
(ab)^3+(bc)^3+(ca)^3=q^3-3pq+3
l'inégalité qu'on veut démontrer devient:
p^3+q^3-6pq+8>=(q-1)^3
<=>p^3+3q^2+9>=6pq+3q
on a déja montrer dans un autre exo que q>=p(c'est facile)
on peut aussi montrer facilement que p^3+3>=4pq et
3q^2>=3q+2pq
(en effet on peut utiliser l'inégalité de Schur et q>=p et p,q>=3).on sommant les deux inégalités pour obtenir le résultat voulu

quel est le problème Mon ami Mahdi,c'est pas trés difficil je pense!!

boukharfane radouane a écrit:: salut tout le monde!
Soient x,y,a et b des réels positifs tels que x#y;x#2y,y#2x,a#3b et
(2x-y)/(2y-x)=(a+3b)/(a-3b).
PROUVER que (x²+y²)/(x²-y²)>=1

on a : x² >= x² et y² >= -y² donc x²+y² >= x²-y²

et on a d'aprés l'ennoncé que : x#y

et pusque x et y sont tout les deux positive donc x # -y

et mnt x²+y² >= x²-y² <=> (x²+y²)/(x²-y²) >= 1

tu ne pense pas Mon ami Conan que tu n'a pas utiliser le fait que (2x-y)/(2y-x)=(a+3b)/(a-3b).

boukharfane radouane a écrit:: tu ne pense pas Mon ami Conan que tu n'a pas utiliser le fait que (2x-y)/(2y-x)=(a+3b)/(a-3b).

mais cite moi mon erreur !

je pense qu'il ya une manque de données,et si vous voulez,je vais changer l'exo!!

boukharfane radouane a écrit:: je pense qu'il ya une manque de données,et si vous voulez,je vais changer l'exo!!

ok vas-y , mais avant tu peux detailler un peu ce que tu as ecrit de Holder

en donnaint par exemple son theoreme ! geek

c'est connue je pense le théorème de Holder,il suffit d'écrire
(a^3+1)(b^3+1)(c^3+1)=(a^3+1)(1+b^3)(1+c^3).

voici un autre exo:

EXERCICE N° 29
trouver tous les réels qui vérifient:
2x*rac(y-1)+2y*rac(z-1)+2z*rac(x-1)>=xy+yz+zx

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

boukharfane radouane a écrit:: c'est connue je pense le théorème de Holder,il suffit d'écrire
(a^3+1)(b^3+1)(c^3+1)=(a^3+1)(1+b^3)(1+c^3).

nn je connais seulement son nom , explique stp

Mon ami Conan,googler sur elle et tu vas trouver les informations que tu cherches!!!

boukharfane radouane a écrit:: Mon ami Conan,googler sur elle et tu vas trouver les informations que tu cherches!!!

$

je l'ai trouvé avec des sigma et PI que je n'ai pas bien comprise Sad

» Grand Jeu d'été (2007 ) TSM __Resultats__
» Grand Jeu d'Hiver TSM 2007-2008
» GRAND COMPETITION D'HIVER TSM 2007-2008!
» c'est un grand grand grand défi
» problème N°75 de la semaine (02/04/2007-08/04/2007)