#Grand Jeu d'été (2007 ) TSM EST COMENCE ==>

Conan a écrit:

boukharfane radouane a écrit:

Mon ami Conan,googler sur elle et tu vas trouver les informations que tu cherches!!!

$

je l'ai trouvé avec des sigma et PI que je n'ai pas bien comprise

l'inégalité de holder

neutrino a écrit:

Conan a écrit:

boukharfane radouane a écrit:

Mon ami Conan,googler sur elle et tu vas trouver les informations que tu cherches!!!

$

je l'ai trouvé avec des sigma et PI que je n'ai pas bien comprise

l'inégalité de holder

je ne pense pas que raduane a parler de cette inégalité !

voila :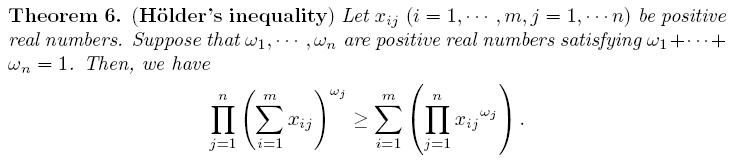



vous pouriez detailler cela

oui c'est ça l'inégalité

boukharfane radouane a écrit:

oui c'est ça l'inégalité

tu peux la detailler seulement sur 3 nombre a et b et c pour mieu comprendre

voila mnt elle est claire





donc Radouane , (a^3+1)(b^3+1)(c^3+1)>= a^3 + (bc)^3

et pas(a^3+1)(b^3+1)(c^3+1)>=(a+bc)^3

en plus tu n'a pas la sum = 1 , alors explique toi

vous voyez pas qu'il faut varier un peu le type des exercices il faut pas proposer juste ceux des inegalités

slt
on a y>=1.x>=1.z>=1
y-1+1>=2rac(y-1)
<=>2xrac(y-1)<=xy (cas d égalité y=2)
pour les autre o6
on deduit que
2xrac(y-1)+2yrac(z-1)+2zrac(x-1)<=xy+yz+zx
avec le seul cas d égalité quand x=y=z=2
donc les seuls nombres sont =y=z=2
a+

pose ton exo Stof

att je cherche.

EXERCICE N° 30
a.b.c>0
montrer que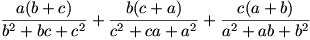
>=2

Lisez ce qui est en rouge avant de répondre

Les reponses doivent etre poster ici du le moment qu'on propose l'exo et le premier qui donne une solution juste avec une démonstration complète aura 2 points et proposera lui aussi un exo et ainsi de suite.
si personne n'as résolu l'exo durant 48 heures alors celui qui à proposer l'exo donnera la solution et proposera un autre

que les inegalités ... yapas que les inegalités dans les maths? je pense que ya d'autres chapitres plus important!!

boukharfane radouane a écrit:

on a:
1/(b²+bc+c²)>=1/(b²+2bc+c²)
=>a(b+c)/(b²+bc+c²)>=a(b+c)/(b+c)²=a/(b+c)
d'où
a(b+c)/(b²+bc+c²)+b(a+c)/(a²+ac+c²)+c(a+b)/(a²+b²+ab)>=a/(b+c)+b/(a+c)+c/(a+b)>=3/2>2.(d'après NESBITT)
d'où la réponse voulu.

je ne crois pas

pourquoi mon ami Selfrespect

on a pas 3>4 amigo lol

pardon.

slt
on a :
a(b+c)/{2(b²+c²+bc)}=a(b+c)/{b²+c²+(b+c)²}
et on a (b+c)²=<2(b²+c²)
alors a(b+c)/{2(c²+b²+bc)}>={1/3}a(b+c)/(b²+c²)
d'autre par on a : (b+c)/(b²+c²)>=1/rac(bc)
donc : a(b+c)/(b²+c²+bc)>={1/3}(a/rac(bc))
de meme les autres puis sommation on obtient:
S/2>= {1/3}(a/rac(bc)+b/rac(ac)+c/rac(ba))>= 1 (IAG)
d'ou S>=2
(je crois que tu dois posté un autre exo 48 h)

selfrespect a écrit:

slt
on a :
a(b+c)/{2(b²+c²+bc)}=a(b+c)/{b²+c²+(b+c)²}
et on a (b+c)²=<2(b²+c²)
alors a(b+c)/{2(c²+b²+bc)}>={1/3}a(b+c)/(b²+c²)
d'autre par on a : (b+c)/(b²+c²)>=1/rac(bc)
donc : a(b+c)/(b²+c²+bc)>={1/3}(a/rac(bc))
de meme les autres puis sommation on obtient:
S/2>= {1/3}(a/rac(bc)+b/rac(ac)+c/rac(ba))>= 1 (IAG)
d'ou S>=2
(je crois que tu dois posté un autre exo 48 h)

nn c pas vrai : car prend par exemple :

b=1 et c=4 ça devien alors : 5/17 >= 1/2 d'ou 10 >= 17 ce qui est faux

bien vu conan

en fait rac(bc)(b+c)-(b²+c²)=-(rac(b)-rac(c))²(..une quantité positif)
en tt cas j'ai essayé de rectifier mais mon pc etait blokéé ..
ben en tt cas il dit poster un nouveau exo ,

selfrespect a écrit:

en fait rac(bc)(b+c)-(b²+c²)=-(rac(b)-rac(c))²(..une quantité positif)
en tt cas j'ai essayé de rectifier mais mon pc etait blokéé ..
ben en tt cas il dit poster un nouveau exo ,

-positive veut dire negatif

on a :

je note S ce qui est en gauche

a(b+c)/[2(b²+c²+bc)]=a(b+c)/[b²+c²+(b+c)²]

et d'aprés C-S on a : 2(b²+c²) >= (b+c)²

donc : a(b+c)/[2(c²+b²+bc)]>=(1/3) a(b+c)/(b²+c²)

et par symetrie de roles on trouves que :

(3/2) S >= a(b+c)/(b²+c²) + b(a+c)/(a²+c²) + c(a+b)/(a²+b²)

et on a :

A = a(b+c)/(b²+c²) + b(a+c)/(a²+c²) + c(a+b)/(a²+b²)

= ((b+c)/a)(a²/(b²+c²)) + ((a+c)/b)(b²/(a²+c²)) + ((a+b)/c)(c²/(a²+b²))

et selon Chebychev :

on a : 3*A >= { (b+c)/a + (a+c)/b + (a+b)/c } { a²/(b²+c²) + b²/(a²+c²) + c²/(a²+b²)}

et selon Nesbitt :


et encore : a²/(b²+c²) + b²/(a²+c²) + c²/(a²+b²) >= 3/2


et on a : (b+c)/a + (a+c)/b + (a+b)/c } >= 6


donc : 3*A >= 3/2 * 6 d'ou A >= 3

et on a : 3/2 S >= A >= 3 d'ou : S >= 2

Conan a écrit:

on a :

je note S ce qui est en gauche

a(b+c)/[2(b²+c²+bc)]=a(b+c)/[b²+c²+(b+c)²]

et d'aprés C-S on a : 2(b²+c²) >= (b+c)²

donc : a(b+c)/[2(c²+b²+bc)]>=(1/3) a(b+c)/(b²+c²)

et par symetrie de roles on trouves que :

(3/2) S >= a(b+c)/(b²+c²) + b(a+c)/(a²+c²) + c(a+b)/(a²+b²)

et on a :

A = a(b+c)/(b²+c²) + b(a+c)/(a²+c²) + c(a+b)/(a²+b²)

= ((b+c)/a)(a²/(b²+c²)) + ((a+c)/b)(b²/(a²+c²)) + ((a+b)/c)(c²/(a²+b²))

et selon Chebychev :

on a : 3*A >= { a/(b+c) + b/(a+c) + c/(a+b) } { a²/(b²+c²) + b²/(a²+c²) + c²/(a²+b²)}

et selon Nesbitt :

on a : a/(b+c) + b/(a+c) + c/(a+b) >= 3/2

et encore : a²/(b²+c²) + b²/(a²+c²) + c²/(a²+b²) >= 3/2

donc : 3*A >= 3/2 * 3/2 d'ou A >= 3/4

et on a : 3/2 S >= A >= 3/4 d'ou : S >= 2

c'et S>=1/2 !!
(ressaye encore )

refais un coup d'oeil, c corriger