| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
+49Loliiiita amigo-6 yasmine yasserito hind nassri tarask Mehdi.O imanos Mlle Betty Xien Arithmysis Miss imane abdrrazak Othmaann oussama1305 Calculus zouhir mizmaz M.Marjani Med oussadan madani reda-t master codex00 Dijkschneier houssa Ayoub M-H sweet-mounir l_Soufiane_l hmima Sylphaen soumitous fmsi majdouline yassine-516 fatima agorram yumi samix rachid18 MohE darkpseudo houssam110 naplhitl radouane_BNE xyzakaria tahiri_soufiane issam erriahi mp23 nmo 53 participants |
|
| Auteur | Message |
|---|
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 04 Mar 2010, 16:14 Jeu 04 Mar 2010, 16:14 | |
| Et voici la solution du deuxième problème:
Posons AC=AB=a.
Donc BF=EC=a et CD=DE=a/2.
On a ABC un triangle rectangle en A.
Donc BC^2=AB^2+AC^2.
Donc BC^2=a^2+a^2.
Donc BC^2=2a^2.
Et on a BCD un triangle rectangle en C.
Donc BD^2=BC^2+DC^2.
Donc BD^2=2a^2+(a/2)^2.
Donc BD^2=2a^2+(a^2)/4.
Donc BD^2=(9a^2)/4.==>(1)
Et on a IED un triangle rectangle en E.
Donc ID^2=IE^2+ED^2.
Donc ID^2=(FE/2)^2+ED^2.
Donc ID^2=(BC/2)^2+ED^2.
Donc ID^2=BC^2/4+(a/2)^2.
Donc ID^2=(2a^2)/4+(a^2)/4.
Donc ID^2=(3a^2)/4.==>(2)
Et on a BFI un triangle rectangle en F.
Donc BI^2=BF^2+FI^2.
Donc BI^2=a^2+IE^2.
Donc BI^2=a^2+(2a^2)/4.
Donc BI^2=(3a^2)/2.==>(3)
Et de 2 et 3 on conclut que BI^2+ID^2=(3a^2)/2+(3a^2)/4.
Donc BI^2+ID^2=(9a^2)/4.
Et on a d'après 1 que BD^2=(9a^2)/4.
Soit en résumé BD^2=BI^2+ID^2.
Et d'après le réciproque du théorème de pytagore, le triangle IBD est rectangle en I.
Donc l'angle BID est droit.
CQFD. sauf faute de frappe. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 04 Mar 2010, 16:26 Jeu 04 Mar 2010, 16:26 | |
| Je vous propose ainsi ces deux problèmes d'algèbre: Problème1:Trouvez x,y, et z des réels vérifiant: z^2-4x=1 et y^2+6z=-17 et x^2+2y=2. Problème2:Le nombre suivant est-il naturel?  . Bonne chance.P.S: ce sont des exercices assez facile. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 09 Mar 2010, 11:47 Mar 09 Mar 2010, 11:47 | |
| Un problème de plus : Problème :Résoudre dans  l'équation suivante :  | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Mar 09 Mar 2010, 13:29 Mar 09 Mar 2010, 13:29 | |
| Slt Dijkschneier  - Dijkschneier a écrit:
- Un problème de plus :
Problème :
Résoudre dans  l'équation suivante : l'équation suivante :
  [/ On simplifier l'equation : V(((x-2030)/22)+1)+V(((x-2030)/21)+1)+V(((x-2030)/20)+1)=V(((x-2030)/2008)+1)+V(((x-2030)/2009)+1)+V(((x-2030))/2010+1) [V(((x-2030)/22)+1)]²=[V(((x-2030))/2010+1)]² Donc : (x-2008)/22=(x-20)/2010 ca veut dire : x=2030 Je vais vérifier si 2030 est la seule solution de l'équation : Si x-2030>0 On a : V(((x-2030)/22)+1)>=V(((x-2030)/2008)+1) V(((x-2030)/21)+1)>=V(((x-2030)/2009)+1) V(((x-2030)/20)+1)>=V(((x-2030))/2010)+1) Donc : V(((x-2030)/22)+1)+V(((x-2030)/21)+1)+V(((x-2030)/20)+1)>=V(((x-2030)/2008)+1)+V(((x-2030)/2009)+1)+V(((x-2030))/2010+1) Posons : x-2030=Y pour plus de simplification ,l'inigalité demeure : V((Y/22)+1)+V((Y/21)+1)+V((Y/20)+1)>=V((Y/2008)+1)+V((Y/2009)+1)+V((Y/2010)+1) Alors: S={2030} Si Y<0 C'est impossible donc : S={} on conclut enfin que la solution de l'equation : S={2030} CQFG | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 | |
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 15:23 Jeu 11 Mar 2010, 15:23 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- Un problème de plus :
Problème :
Résoudre dans  l'équation suivante : l'équation suivante :
 Je vous attends )) j'espére que c'est juste. Ta solution ne semble pas être parfaite. Il te faut discuter pour cette équation plus de 6 cas. Il existe une équation plus célèbre, la voici:  . A laquelle on donne une solution un peu biarre. Je présente dans mon prochain message une belle solution pour celle de Dijkschneier. C'est une methode qu'un ami m'a appri il y deux semaines. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 16:12 Jeu 11 Mar 2010, 16:12 | |
| - Dijkschneier a écrit:
Problème :
Résoudre dans  l'équation suivante : l'équation suivante :
 . On a  . Donc  . Donc  . D'autre part, on a  . Donc  . Donc }{\sqrt{\frac{x-2008}{22}}%20+%20\sqrt{\frac{x-22}{2008}}%20}) . Donc  \frac{1986}{\sqrt{\frac{x-2008}{22}}%20+%20\sqrt{\frac{x-22}{2008}}%20}) . De même on a  \frac{1988}{\sqrt{\frac{x-2009}{21}}%20+%20\sqrt{\frac{x-21}{2009}}%20}) . Et ausi on a \frac{1990}{\sqrt{\frac{x-2010}{20}}%20+%20\sqrt{\frac{x-20}{2010}}%20}) . Revenons à notre équation: On a  . Donc  \frac{1986}{\sqrt{\frac{x-2008}{22}}%20+%20\sqrt{\frac{x-22}{2008}}%20}+(x-2038) \frac{1988}{\sqrt{\frac{x-2009}{21}}%20+%20\sqrt{\frac{x-21}{2009}}%20}+(x-2038)\frac{1990}{\sqrt{\frac{x-2010}{20}}%20+%20\sqrt{\frac{x-20}{2010}}%20}=0) . Donc  \Biggggg ( \frac{1986}{\sqrt{\frac{x-2008}{22}}%20+%20\sqrt{\frac{x-22}{2008}}%20}+\frac{1988}{\sqrt{\frac{x-2009}{21}}%20+%20\sqrt{\frac{x-21}{2009}}%20}+\frac{1990}{\sqrt{\frac{x-2010}{20}}%20+%20\sqrt{\frac{x-20}{2010}}%20} \Biggggg )=0) . Donc 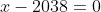 . Car  est toujours positifs. Donc 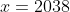 . CQFD. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 16:19 Jeu 11 Mar 2010, 16:19 | |
| Pour le premier:
On a z^2-4x=1 et y^2+6z=-17 et x^2+2y=2.
Soit en sommant: z^2-4x+y^2+6z+x^2+2y=1-17+2.
Donc z^2+6z+x^2-4x+y^2+2y=-14.
Donc z^2+6z+x^2-4x+y^2+2y+14=0.
Donc z^2+6z+9+x^2-4x+4+y^2+2y+1=0.
Donc (z+3)^2+(x-2)^2+(y+1)^2=0.
Donc (z+3)^2=0 et (x-2)^2=0 et (y+1)^2=0.
Donc z+3=0 et x-2=0 et y+1=0.
Donc z=-3 et x=2 et y=-1.
Est-ce difficile? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 16:39 Jeu 11 Mar 2010, 16:39 | |
| Pour le deuxième: Posons  . On a  . Donc  . Donc ^2-2\sqrt{3}+1^2}+\sqrt{(4\sqrt{3})^2-2*7*4\sqrt{3}+7^2}) . Donc ^2} +\sqrt{(4\sqrt{3}-7)^2}) . On a 3>1. Donc V3>1. Donc V3 -1>0. Donc ^2}=4(\sqrt{3}-1)) . Donc ^2}=4\sqrt{3}-4) . Et on a 49>48. Donc V49>V48. Donc 7>4V3. Donc 0>4V3 -7. Donc ^2}=7-4\sqrt{3}) . Revenons à A: On a ^2} +\sqrt{(4\sqrt{3}-7)^2}) . Donc  . Et finalement 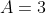 . Donc le nombre proposé est naturel. Est-ce difficile? | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 16:45 Jeu 11 Mar 2010, 16:45 | |
| Je vous propose ainsi ce problème, éspérant qu'il soit à la hauteur:
Soit x un réel non nul vérifiant x^2=4x-1.
Calculez x^3+x^2+x+1/x+1/x^2+1/x^3.
Bonne chance.
Celui ou celle qui répond poste un autre exercice.
P.S: c'est un exercice très facile. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 11 Mar 2010, 19:11 Jeu 11 Mar 2010, 19:11 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Dim 14 Mar 2010, 00:03 Dim 14 Mar 2010, 00:03 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Dijkschneier a écrit:
- Un problème de plus :
Problème :
Résoudre dans  l'équation suivante : l'équation suivante :
 Je vous attends )) j'espére que c'est juste. Ta solution ne semble pas être parfaite.
Il te faut discuter pour cette équation plus de 6 cas.
Il existe une équation plus célèbre, la voici:
Slt nmo , oui ;il ya plusieurs methodes , mais il suffit de discuter sur Y>0 et Y<0 dans mon cas pour voir s'il y avait d'autres solutions sue |R. T'as une belle methode ,le probléme qu'on a trouver les S différents! dans ce cas x=2030 non ? et dans le probléme que tu m'as donné x=10. Il ya une autre methode mais avec les outils mathématics de premiére. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 18 Mar 2010, 19:12 Jeu 18 Mar 2010, 19:12 | |
| Encore une fois personne ne répond, voici la solution:
On a x^2=4x-1.
Donc x^2+1=4x.
Donc (x^2+1)/x=4x/x.
Donc x^2/x + 1/x=4.
Donc x+1/x=4.==>(1)
Donc (x+1/x)^2=4^2.
Donc x^2+2x*1/x+1/x^2=16.
Donc x^2+2+1/x^2=16.
Donc x^2+1/x^2=14.==>(2)
En multipliant 1 et 2, on trouve (x^2+1/x^2)(x+1/x)=14*4.
Donc x^3+x+1/x+1/x^3=56.
Donc, par addition de 1, on trouve x^3+x+1/x+1/x^3+x+1/x=56+14.
Donc x^3+x^2+x+1/x+1/x^2+1/x^3=70.
C'était facile. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 18 Mar 2010, 19:25 Jeu 18 Mar 2010, 19:25 | |
| Même s'il est facile, voici mon exercice: ABC triangle avec des angles aigus, h est son hauteur passant par A, posons a=BC et AC=b et c=AB. Prouver que:  Bonne chance. Bonne chance. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 18 Mar 2010, 20:26 Jeu 18 Mar 2010, 20:26 | |
| - nmo a écrit:
- nmo.[/b]
Dsl , j'avais 4 devoirs cette semaine donc j'avais trop peu de temps, c'est pourquoi j'arrive pas à vous partager ici. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 25 Mar 2010, 18:41 Jeu 25 Mar 2010, 18:41 | |
| - nmo a écrit:
- ABC triangle avec des angles aigus, h est son hauteur passant par A, posons a=BC et AC=b et c=AB.
Prouver que: 
[b]b] soit H le projeté orthogonal de A sur [BC] (BH-CH)²>=0 BH²+CH²-2BH*CH>=0 2BH²+2CH²-(BH+CH)²>=0 2BH²+2CH²-a²>=0 Donc : BH²=c²-h² CH²=b²-h² Don't le résultat. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Jeu 25 Mar 2010, 18:49 Jeu 25 Mar 2010, 18:49 | |
| problème proposé: soient a b et c des réels distincts. montrer que:  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 11:43 Sam 27 Mar 2010, 11:43 | |
| - M.Marjani a écrit:
- problème proposé:
soient a b et c des réels distincts.
montrer que:
 Tout d'abord, posons m=b/a et n=c/b et p=a/c. On a mnp=b/a*c/b*a/c. Donc mnp=1. Donc b=am et c=bn et a=cp. On veut démontrer que ^2+(\frac{b}{b-c})^2+(\frac{c}{c-a})^2 \ge 1) . C'est à dire ^2+(\frac{b}{b-bn})^2+(\frac{c}{c-cp})^2 \ge 1) . C'est à dire })^2+(\frac{b}{b(1-n)})^2+(\frac{c}{c(1-p)})^2 \ge 1) . C'est à dire ^2+(\frac{1}{1-n})^2+(\frac{1}{1-p})^2 \ge 1) . On pose 1-m=x et 1-n=y et 1-p=z. Donc m=1-x et n=1-y et p=1-z. Et on a mnp=1. Donc (1-x)(1-y)(1-z)=1. Donc (1-y-x+xy)(1-z)=1. Donc 1-z-y+yz-x+xz+xy-xyz=1. Donc xy+zx+zy=x+y+z+xyz. Donc (xy+zx+zy)^2=(x+y+z+xyz)^2. Donc (xy)^2+(zx)^2+(zy)^2+2xy*zx+2xy*zy+2zx*zy=(x+y+z)^2+(xyz)^2+2xyz(x+y+z). Donc (xy)^2+(zx)^2+(zy)^2+2x*yzx+2xyz*y+2zxy*z=(x+y+z)^2+(xyz)^2+2xyz(x+y+z). Donc (xy)^2+(zx)^2+(zy)^2+2xyz(x+y+z)=(x+y+z)^2+(xyz)^2+2xyz(x+y+z). Donc (xy)^2+(zx)^2+(zy)^2=(x+y+z)^2+(xyz)^2. Donc (xy)^2+(zx)^2+(zy)^2-(xyz)^2=(x+y+z)^2. D'autre part, on a 0=<(x+y+z)^2. Donc 0=<(xy)^2+(zx)^2+(zy)^2-(xyz)^2. Donc (xyz)^2=<(xy)^2+(zx)^2+(zy)^2. En divisant par (xyz)^2 on obtient 1=<(1/x)^2+(1/y)^2+(1/z)^2. Donc ^2+(\frac{1}{1-n})^2+(\frac{1}{1-p})^2 \ge 1) . Donc ^2+(\frac{b}{b-c})^2+(\frac{c}{c-a})^2 \ge 1) . CQFD. Sauf faute de frappe. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 11:48 Sam 27 Mar 2010, 11:48 | |
| Problèmes propposés: Résolvez en IR les deux équation suivantes: ^2}=3) .  . Bonne chance.P.S: les deux équations sont indépendantes. | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 13:09 Sam 27 Mar 2010, 13:09 | |
| Pour le 2éme on a 0<x<144 Et :   Le 1er possibilité don x=9 la 2éme n'admet pas de solution positif . Ps: Pour la 2éme on pose X=V(12-Vx) | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 13:14 Sam 27 Mar 2010, 13:14 | |
|
Dernière édition par M.Marjani le Dim 27 Fév 2011, 02:05, édité 1 fois | |
|
  | |
mizmaz
Maître
 Nombre de messages : 234 Nombre de messages : 234
Age : 31
Date d'inscription : 24/10/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 13:41 Sam 27 Mar 2010, 13:41 | |
| Pour la première : ^2}%20=%203%20\Leftrightarrow%20x^2+\frac{x^2}{x^2-2x+1}-3=0%20\Leftrightarrow%20\frac{x^2(x^2-2x+1)+x^2-3(x^2-2x+1)}{(x-1)^2}%20=%200%20\Leftrightarrow%20\frac{x^4-2x^3+x^2%20+%20x^2-3x^2+6x-3}{(x-1)^2}%20=%200%20\Leftrightarrow%20\frac{x^4-2x^3-x^2+6x-3}{(x-1)^2}=0%20\Leftrightarrow%20\frac{(x^2-3x+3)(x^2+x-1)}{(x-1)^2}%20=%200%20\Rightarrow%20S=\begin{Bmatrix}%20-\frac{1+\sqrt{5}}{2},\frac{-1+\sqrt{5}}{2}%20\end{Bmatrix}) Sauf erreur !  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 13:48 Sam 27 Mar 2010, 13:48 | |
| Deux autres, tant qu'on y est : Problème 1 :Résoudre dans [0; 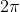 ] l'inéquation : }}\geq%20\sqrt{2}\cos{(2x)}) . Problème 2 :Soit ABC un triangle. a,b et c sont ses longueurs de côté, et alpha, bêta et gamma ses angles respectifs. Montrez que : (\cos{\alpha}+\cos{\beta}+\cos{\gamma}-1)) . | |
|
  | |
Sylphaen
Expert sup

 Nombre de messages : 555 Nombre de messages : 555
Age : 30
Localisation : Rabat
Date d'inscription : 30/11/2009
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 14:03 Sam 27 Mar 2010, 14:03 | |
| La factorisation est un peu magik ^^ sinon voici une autre solution pour l'équation : On fixe y=1/x on se ramène à : 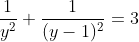 Pour équilibrer ( avoir une équation de 2éme degré) on pose z=y-1/2 Ca donne : 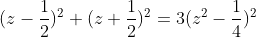 encore un changement de variable : a=z²>=0 ca donne : 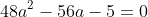 La solution positif est a=5/4 Puis on trouve aisément les valeurs de x | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  Sam 27 Mar 2010, 16:30 Sam 27 Mar 2010, 16:30 | |
| - mizmaz a écrit:
- Pour la première :
^2}%20=%203%20\Leftrightarrow%20x^2+\frac{x^2}{x^2-2x+1}-3=0%20\Leftrightarrow%20\frac{x^2(x^2-2x+1)+x^2-3(x^2-2x+1)}{(x-1)^2}%20=%200%20\Leftrightarrow%20\frac{x^4-2x^3+x^2%20+%20x^2-3x^2+6x-3}{(x-1)^2}%20=%200%20\Leftrightarrow%20\frac{x^4-2x^3-x^2+6x-3}{(x-1)^2}=0%20\Leftrightarrow%20\frac{(x^2-3x+3)(x^2+x-1)}{(x-1)^2}%20=%200%20\Rightarrow%20S=\begin{Bmatrix}%20-\frac{1+\sqrt{5}}{2},\frac{-1+\sqrt{5}}{2}%20\end{Bmatrix})
Sauf erreur !  Bonne réponse mizmaz , une petite remarque S={(-1+V5)/2;1;(-1-V5)/2} Car : Dans le premier on va trouver que : S={} et l'autre : S={(1+V5)/2;(-1-V5)/2} et l'autre : (x-1)²=0 <=> x=1 <=> S={1} Donc : S={(1+V5)/2;(-1-V5)/2;1} Bonne chance. | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010) Sujet: Re: Préparations aux olympiades de tronc commun (2009-2010)  | |
| |
|
  | |
| | Préparations aux olympiades de tronc commun (2009-2010) |  |
|
