Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)

Elle est vraiment moche ma soluce pour cet exo // Quand on introduit des fonctions en arithmétiques ça devient

le plus important c'est qu'elle soit correct , tu peux la poster si tu veux

memath a écrit:

en attendant une reponse correct je propose un autre exo :

trouver tous les entiers strictement positifs x et y tel que :

x+y²+z^3=xyz et z=pgcd(x,y)

petite indication : disjonction des cas ,z=1, z=x , z=y

qu'est ce que ça veut dire LHS et RHS?

Left hand side et right hand side.

memath a écrit:

en attendant une reponse correct je propose un autre exo :

trouver tous les entiers strictement positifs x et y tel que :

x+y²+z^3=xyz et z=pgcd(x,y)



Ps: ici on ne poste que la solution , qui doit de preference etre correct !!
vos approches sont les bienvenus sauf qu'ils doivent etre signalé comme etant que des approches , merci.

C'est un problem shortlist 1995 je laisse la chance aux autres pour rechercher

en citant la source tu leurs a privé de leurs chances.
poste la soluce puis un autre exo
ps:la solution officielle est trés moche , il existe bcp plus elegant

Toutes mes excuses memath je voulais seulement au lieu d'ecrire toute la solution que si qqun veut la solution de ce problème il suffit de rechercher dans le shortlist 1995 car ca fait un bon moment que personne n'a resolut ce problème Donc je vais poster un nouveau exo :

Montrer que pour tt a,b,c les longeurs d'un triangle on a

a^3+b^3+3abc> c^3

Abdek_M a écrit:

Toutes mes excuses memath je voulais seulement au lieu d'ecrire toute la solution que si qqun veut la solution de ce problème il suffit de rechercher dans le shortlist 1995 car ca fait un bon moment que personne n'a resolut ce problème Donc je vais poster un nouveau exo :

Montrer que pour tt a,b,c les longeurs d'un triangle on a

a^3+b^3+3abc> c^3

l'inegalité etant trés faible une trés bonne question serai de determiner le minimum de LHS-RHS

a,b et c étant les longueurs des côtés d'un triangle, il est possible de réaliser la substitution de Ravi. Soit donc 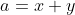, 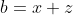et 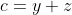où x,y et z sont des réels strictement positifs.
Ainsi, l'inégalité à démontrer est équivalente à :

qui est largement vraie.

c juste mais il existe une solution plus élegante en 1 ligne tu peux posté un nouveau exo

Avec une autre solution on a :

a³+b³=(a+b)((a+b)²-3ab))
>c(c²-3ab) =c³-3abc

D'où la conclusion

On a :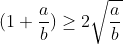

D'où :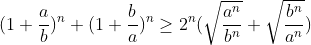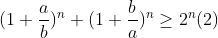



Puis conclure ..

En effet, une simple identité remarquable...

Sylphaen poste ton nouveau exo

Permettez moi de poster ce probleme.
a,b,c,d,e>0
tel que a²+b²+c²=d²+e² et a^4+b^4+c^4=d^4+e^4
comparer a^3+b^3+c^3 et e^3+d^3

vous pouvez continuer le jeu sans resoudre ce probleme car il est vraiment assez compliqué.
mais ca reste un bon entrainement pour l'imo et celui qui l'aura il aura une forte chance pour avoir une medaille d'or
Bonne chance.

Voilà pour changer un peu j'ai choisi celui de géo ^^

Dans la figure, (CC') ne semble pas perpendiculaire à (AB). Ça a été fait exprès ?

Bof tu sais l'énoncé suffit , on s'en fou pas mal de la figure puisqu'on peux la tracer nous même.

Soit et les projections hortoghonales des points sur les coté opposés Il est clair que donc les points sont cocycliques il s'ensuit que et comme et alors les triangles et sont egaux donc et Posons donc on a donc le triangle est rectangle. il s'ensuit que car AC'B' est isocel
et d'autre part on a et et donc les triangles et sont egaux d'ou et et posons donc on a donc le triangle est rectangle et donc

de 1 et 2 on en déduit que d'ou la le resultat

memath a écrit:

voici un autre jolie probleme en attendant une solution pour le precedant :

quel est la valeur de k et des reels x1 , x2, ....xk tel que leurs somme egal à 100 et leur produit est maximal.

wa feen a bba mehdi

si j'ai bien compris ton beau pb , je pense que ce k et les x_i n'existent pas;

supposons que ce k et ces reels existent ; alors le produit x_1*x_2*..........x_k=P ( avec sum(x_i)=100) est maximale

considerons les nombres x_1;x_2;.........x_k, x_k;-x_k leur somme vaut 100 , alors P * ( x_1) *(-x_1) <= P cequi montre que P est postif

soit a_1,a_2........a_p des reels tq leur somme est nulle , donc x_1+....x_k+a_1+.....a_p=100 donc P*prod ( a_p) <= P et comme P est positif , alors prod(a_p)<=1 ce qui n'est pas tjrs vrai ....

P.S : positif = stictement positif , car P est clairement non nul
(sauf erreur)
A+

Tu peux poster un exo Abdek ^^

Voila un e xo tré facile de geometrie:
Soit ABCD un quadrilatère de coté a et b et c et d Montrer que l'aire de ABCD est inferieur ou égal à ac + bd/2

On pose :
BC=a
CD=b
AD=c
AB=d
On a :
S=S(ABD)+S(BCD)
S=1/2 ( cd Sin  + ab Sin C )

S ≤ 1/2 (ab+cd) car |Sin(x)|≤1