| | Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) |  |
|
+23Smaeiil.B Sylphaen samix Othmaann Abdek_M Dijkschneier Yassino codex00 MohE houssa just-abdess hindou11 beautiful mind l3arbi MissBac Figo memath S.Freud rachid18 . EINSTEINIUM Thalès Perelman 27 participants |
|
| Auteur | Message |
|---|
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Lun 14 Déc 2009, 22:43 Lun 14 Déc 2009, 22:43 | |
| oui,pour ordonner les variables il faut que l'expression soit cyclique ou symetrique.. | |
|
  | |
Thalès
Expert grade1

 Nombre de messages : 400 Nombre de messages : 400
Age : 32
Localisation : Casablanca
Date d'inscription : 15/05/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Lun 14 Déc 2009, 22:52 Lun 14 Déc 2009, 22:52 | |
| Je viens d'éditer mon post en expliquant ma démarche. | |
|
  | |
beautiful mind
Maître

 Nombre de messages : 117 Nombre de messages : 117
Age : 33
Date d'inscription : 01/04/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mar 15 Déc 2009, 14:42 Mar 15 Déc 2009, 14:42 | |
| Sans utiliser tous ce que vous avez établit je vous propose cette solution magique,
Sum(1/ai)Sum(ai/(i²))>=(Sum(1/i))²
Or,
Sum(1/ai)<=1+1/2+......+1/n(On s'en fout de leur ordre!)
Donc,
Sum(ai/(i²))>=(Sum(1/i))²/(Sum(1/i))=Sum(1/i). | |
|
  | |
EINSTEINIUM
Maître

 Nombre de messages : 245 Nombre de messages : 245
Age : 31
Localisation : Oujda
Date d'inscription : 29/01/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mar 15 Déc 2009, 19:27 Mar 15 Déc 2009, 19:27 | |
| Je crois qu'il est temps de poster la solution puisque presque 24 heures s"est écoulé : Solution :Comme 0 et 1 appartiennent à E alors 1/2 appartient à E. supposons aue Card(E)>3 et soit c un élement de E et c £ ]1/2,1[ on va prouver que c=2/3. supposons que c#2/3 en prenons c tel que |c-2/3| soit minimale (ce qui est impossible car E est finit) comme c>1/2 alors c/2 £ E et c/2<1/2 et on en déduit que (c/2 +1)/2 £ E. mais |(c/2 +1)/2 -2/3|=1/4|c- 2/3| ce qui est impossible . on démontre de meme que E intersection ]0,1/2[={1/3} donc cardE=<5 et l'ensemble maximal est {0,1/3,1/2,2/3,1} Voila un Problème assez facile: soit x_1,x_2,x_3...x_n des réels positif et n>1 tel que:  Montrer que :  | |
|
  | |
memath
Expert sup

 Nombre de messages : 1645 Nombre de messages : 1645
Age : 32
Localisation : oujda
Date d'inscription : 17/02/2007
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mer 16 Déc 2009, 19:36 Mer 16 Déc 2009, 19:36 | |
| je donne un indice pour avancer  - Spoiler:
x --> 1/(1+e^x) est convexe et qui dit convexe dit...
| |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mer 16 Déc 2009, 21:10 Mer 16 Déc 2009, 21:10 | |
| slt!! oui memath,j'ai touché au environs de Ln mais j'ai pas tombé dans sa réciproque ^^.ca va donner immédiatement avec jensen. je propose maintenant le problème suivant: trouver tt les fonctions f en déterminant B tel que:   a£IR a£IR. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mer 16 Déc 2009, 21:36 Mer 16 Déc 2009, 21:36 | |
| ^{\frac{1}{n}}%20\geq%20n-1%20\Leftrightarrow%20\frac{1}{n}\sum%20x_{i}%20\geq%20\ln%20\left%20(n-1%20\right%20)) Or,  , donc ) d'après Cauchy-Schwartz, d'où 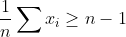 (n est non nul). Mais il est clair que ) , d'où la conclusion. | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mer 16 Déc 2009, 21:58 Mer 16 Déc 2009, 21:58 | |
| slt Dijkschneier  dans la premiere ligne: 1/n.sum{ Ln{x_i}}... | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Mer 16 Déc 2009, 22:18 Mer 16 Déc 2009, 22:18 | |
| Effectivement, ma démonstration est erronée. | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Jeu 17 Déc 2009, 14:05 Jeu 17 Déc 2009, 14:05 | |
| slt hamza !!
pour ton e.f:
on va vraiment poser T(x)=(1/(x-a)+a) de IR-{a} ---> IR-{a}.
puisque T(T(x)) =x pr tt x £ IR-{a} donc T est une involution
ce qu'on en déduit que :
f(x)=A(x,T(x)) avec A est une fonction symetrique de IR-{a} ---> IR
il existe une infinitée de tel fonction , par exemple:
f(x)=xT(x) ; f(x)=x+T(x) ... | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Jeu 17 Déc 2009, 14:07 Jeu 17 Déc 2009, 14:07 | |
| bien joué redwan lol (les mémoires  ) poste un exo  | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Jeu 17 Déc 2009, 14:37 Jeu 17 Déc 2009, 14:37 | |
| Oui hamza les mémoires lol  je vais proposer une e.f : Trouver toutes les fonction de IR--->IR telles que : pr tt xy £ IR : f(xy)=f(x)f(y) | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:04 Ven 18 Déc 2009, 17:04 | |
| salut , peut etre cette e.f et un peu dure .
c'est vrai que l'e.f satisfait f(x)=x .
j'ai une solution intuitive ,mais qui manque du précision .
j'en suis pas sur . | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:17 Ven 18 Déc 2009, 17:17 | |
| - . a écrit:
- salut , peut etre cette e.f et un peu dure .
c'est vrai que l'e.f satisfait f(x)=x .
j'ai une solution intuitive ,mais qui manque du précision .
j'en suis pas sur . peut etre que l'e.f lui manque qq conditions... je propose un nouveau pb pour continuer: Problème. Montrer que pour (a,b,c)>0 tel que:  on a:  | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:34 Ven 18 Déc 2009, 17:34 | |
| Posons   et  L'inegalité est equivalente à  par cauchy  il suffit de prouver que  ou bien  ce qui est immediat par am gm puisque xyz=1 Problème : Montrer que pour a,b,c les longuers d'un triangle on a : a/(b+c)+b/(a+c)+c/(a+b)<2 | |
|
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:35 Ven 18 Déc 2009, 17:35 | |
| Si vous en avez le temps et la patience. Que signifie cyc en dessous du Sigma ? | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:36 Ven 18 Déc 2009, 17:36 | |
| On pose 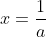 , 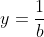 , et 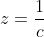 . Ainsi, on a 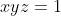 et l'inégalité devient :  Or, ^{2}}{2(x+y+z)}&space;=&space;\frac{x+y+z}{2}&space;\geq&space;\frac{3(xyz^{\frac{1}{3}})}{2}&space;=&space;\frac{3}{2}) , d'après C.S + IAG CQFD | |
|
  | |
hindou11
Maître

 Nombre de messages : 148 Nombre de messages : 148
Age : 32
Date d'inscription : 28/03/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:38 Ven 18 Déc 2009, 17:38 | |
| bonjour
[1/a^3(b+c)]+ [1/ b^3(a+c)] +[1/ c^3 (a+b)] >= 3*3^V[(1/a^3(b+c))*(1/ b^3(a+c))*(1/ c^3 (a+b))] (*)
& a^3(b+c)>=2a²
b^3(a+c)>=2b²
c^3 (a+b)>=2c²
on remplace dans (*)
1/a^3(b+c) + 1/ b^3(a+c) + 1/ c^3 (a+b) >= 3*3^V[1/8a²b²c²]
1/a^3(b+c) + 1/ b^3(a+c) + 1/ c^3 (a+b) >=3/2
désolée j'ai pas vu ton message dj ^^ | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:43 Ven 18 Déc 2009, 17:43 | |
| +(b+c)}&space;<&space;2) Or, +(b+c)&space;>&space;a+b+c&space;\Leftrightarrow&space;\frac{2a}{(b+c)+(b+c)}&space;<&space;\frac{2a}{a+b+c}) d'après l'inégalité triangulaire. D'où +(b+c)}&space;<&space;\frac{2(a+b+c)}{a+b+c}&space;=&space;2) | |
|
  | |
Perelman
Expert sup
 Nombre de messages : 2013 Nombre de messages : 2013
Age : 33
Localisation : kenitra
Date d'inscription : 08/02/2008
 | |
  | |
Othmaann
Expert grade1
 Nombre de messages : 444 Nombre de messages : 444
Age : 32
Localisation : Rabat
Date d'inscription : 15/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 17:58 Ven 18 Déc 2009, 17:58 | |
| | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 | |
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 18:12 Ven 18 Déc 2009, 18:12 | |
| on a par Cauchy shwarz et Am-Gm:  et d'ou le resultat | |
|
  | |
Abdek_M
Maître

 Nombre de messages : 162 Nombre de messages : 162
Age : 31
Localisation : France
Date d'inscription : 18/12/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Ven 18 Déc 2009, 18:17 Ven 18 Déc 2009, 18:17 | |
| Problème a,b,c>0: Montrer que  | |
|
  | |
.
Maître
 Nombre de messages : 296 Nombre de messages : 296
Age : 33
Localisation : Maroc.
Date d'inscription : 18/08/2009
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  Sam 19 Déc 2009, 00:24 Sam 19 Déc 2009, 00:24 | |
| premièrement on va poser a=tb et b=t'c (avec  ) donc a=tt'c et b=t'c et c=c , remplaçons ces valeur dans notre inegalité et on obtient :  aprés bcp de calcul on obtient :  maintenent on va presiser [ A(t)-B(t) ]' de façon à etudier la monotonie de A(t)-B(t) !!  donc : [ A(t)-B(t) ] est strictement croissante sur  donc :  ce qui est clairment vrai puisque  . avec l'igalité si t=t'=1 ou bien a=b=c . je sais pas si j'ai fait des fautes de calcule mais la methode reste toujours vrai  . je veux une verification ! | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) Sujet: Re: Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.)  | |
| |
|
  | |
| | Grand Jeu d'Hiver 2009-2010.(préparation à l'imo 2010.) |  |
|
