| | Préparations aux olympiades de première (2010-2011) |  |
|
+37mtb ali-mes n.naoufal King expert_run Mehdi.A Sylphaen Nayssi amigo-6 kaj mima Misterayyoub boubou math az360 zouhir YIRA mayback princessdesmaths darkpseudo ayoubmath mizmaz yasserito tahasinbad Sweetk Nettah108 mathslover Othmaann Mehdi.O soumitous W.Elluizi tarask Sporovitch M.Marjani chamitos007 -Crash- nmo louis Dijkschneier 41 participants |
|
| Auteur | Message |
|---|
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 05 Avr 2011, 22:36 Mar 05 Avr 2011, 22:36 | |
| - nmo a écrit:
- W.Elluizi a écrit:
- On obtient alors de l'inégalité triangulaire que:
 Il faut le démontrer. Pour ce faire,rien de plus simple qu'une récurrence sur n: Admettons en un premier temps que:  donc:  Et on posant encore:  On ré-applique l'inégalité triangulaire:  Et le résultat en découle. | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 05 Avr 2011, 22:57 Mar 05 Avr 2011, 22:57 | |
| | |
|
  | |
W.Elluizi
Maître

 Nombre de messages : 153 Nombre de messages : 153
Age : 30
Date d'inscription : 21/04/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Mar 05 Avr 2011, 23:16 Mar 05 Avr 2011, 23:16 | |
| Je ne dispose actuellement d'aucun problème comportant de l'intérêt,donc que chacun se sente libre d'en poster un. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 13:34 Ven 08 Avr 2011, 13:34 | |
| Je propose: Exercice 87:Trouvez le plus petit entier n tel que  et n est compris entre 1000 et 1111. Bonne chance. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 13:46 Ven 08 Avr 2011, 13:46 | |
| Je parie qu'il s'agit là aussi d'un problème marocain  | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 13:54 Ven 08 Avr 2011, 13:54 | |
| - M.Marjani a écrit:
- Dijkschneier a écrit:
- d=pgcd(x,y), x=dx', y=dy'
d² | d²x'y' = xy | x²+y²-x = d²x'² + d²y'² - dx' ===> d² | dx' ===> d|x' ===> x'=dx'' ===> x=d²x''²
x | xy | x²+y²-x ===> x | y² ===> d²x'' | d²y'² ===> x'' | y'²
x'' et y'² premiers entre eux ===> x''=1
Done ! Pour quelle raison les deux naturelles x" et y'² sont premiers entre eux ? Je crois avoir trouvé une réponse à cette question: On pose: k=PGCD(x,y²), on a d'un côté: k=PGCD(x,y²)=PGCD(d².x'',d².y'²)=d².PGCD(x'',y'²). Et d'un autre côté: &\Rightarrow k/x\text{ et }k/y^2\\&\Rightarrow k/x^2\text{ et }k/y^2\\&\Rightarrow k/x^2\wedge y^2\\&\Rightarrow k\wedge (x^2\wedge y^2)=k\\&\Rightarrow k\wedge d^2=k\\&\Rightarrow \big(d^2.(x''\wedge y'^2)\big)\wedge d^2=d^2.(x''\wedge y'^2)\\&\Rightarrow d^2.\big((x''\wedge y'^2)\big)\wedge 1=d^2.(x''\wedge y'^2)\\&\Rightarrow \big((x''\wedge y'^2)\big)\wedge 1=x''\wedge y'^2\\&\Rightarrow x''\wedge y'^2=1\end{align*}) . Donc x'' et y'² sont premiers entre eux. Sauf erreur. | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 14:01 Ven 08 Avr 2011, 14:01 | |
| Pourquoi tant de peine nmo ?
Puisque x' et y' sont premiers entre eux, alors x' et y' ne partagent aucun facteur en commun, et donc leurs diviseurs à fortiori n'en partagent pas non plus !!
La morale, c'est de toujours utiliser la décomposition en facteurs premiers pour vérifier mentalement la primalité entre deux entiers...
Tout comme le ferait un algorithme simpliste... | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 14:03 Ven 08 Avr 2011, 14:03 | |
| - Dijkschneier a écrit:
- Je parie qu'il s'agit là aussi d'un problème marocain
 Je ne suis pas au courant de sa source, mais il est ennuyeux. Je sais la procédure de résolution, que je vais écrire après deux jours si personne ne me devance. Et voici un problème de plus: Problème 88:Soit a et b deux entiers naturels tel que 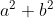 soit premier. Démontrez que l'équattion  n'admet pas de solutions entières. Bonne chance. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 14:35 Ven 08 Avr 2011, 14:35 | |
| a^2-4b-4 = p - b^2-4b-4 = p-(b+2)^2
Il faut que ce nombre soit un carré parfait CAD p = x^2+(b+2)^2 or on a déjà
p= a^2+b^2 et on sait d'après le théorème des deux carré qu'un nombre premier p =1[4] s'écris de façon unique sous la forme de deux carré
donc a = b+2 et x=b donc p = b^2+(b+2)^2 = b^2+b^2+4b+4 qui est pair et ceci est une contradiction avec le fait que p soit premier et p ne peut être égal à 2 car 2b^2+4b+4 > 2 . | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 14:42 Ven 08 Avr 2011, 14:42 | |
| | |
|
  | |
M.Marjani
Expert sup

 Nombre de messages : 1665 Nombre de messages : 1665
Age : 30
Date d'inscription : 05/03/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 14:59 Ven 08 Avr 2011, 14:59 | |
| - nmo a écrit:
- M.Marjani a écrit:
- Dijkschneier a écrit:
- d=pgcd(x,y), x=dx', y=dy'
d² | d²x'y' = xy | x²+y²-x = d²x'² + d²y'² - dx' ===> d² | dx' ===> d|x' ===> x'=dx'' ===> x=d²x''²
x | xy | x²+y²-x ===> x | y² ===> d²x'' | d²y'² ===> x'' | y'²
x'' et y'² premiers entre eux ===> x''=1
Done ! Pour quelle raison les deux naturelles x" et y'² sont premiers entre eux ? Je crois avoir trouvé une réponse à cette question:
On pose: k=PGCD(x,y²), on a d'un côté: k=PGCD(x,y²)=PGCD(d².x'',d².y'²)=d².PGCD(x'',y'²).
Et d'un autre côté:
&\Rightarrow k/x\text{ et }k/y^2\\&\Rightarrow k/x^2\text{ et }k/y^2\\&\Rightarrow k/x^2\wedge y^2\\&\Rightarrow k\wedge (x^2\wedge y^2)=k\\&\Rightarrow k\wedge d^2=k\\&\Rightarrow \big(d^2.(x''\wedge y'^2)\big)\wedge d^2=d^2.(x''\wedge y'^2)\\&\Rightarrow d^2.\big((x''\wedge y'^2)\big)\wedge 1=d^2.(x''\wedge y'^2)\\&\Rightarrow \big((x''\wedge y'^2)\big)\wedge 1=x''\wedge y'^2\\&\Rightarrow x''\wedge y'^2=1\end{align*}) . .
Donc x'' et y'² sont premiers entre eux.
Sauf erreur. Bien. Une bonne rédaction. - Dijkschneier a écrit:
- Puisque x' et y' sont premiers entre eux, alors x' et y' ne partagent aucun facteur en commun.
C'est ce que je cherche. Si c'étaient x' et y' premiers nous dirige directement à dire que x'' et y' premiers entre eux ce que tu n'as pas supposer au début. La solution reste trés jolie en fait.  | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 19:41 Ven 08 Avr 2011, 19:41 | |
| Problème 89 :
Bon voila un lemme très intéressant :
Prouvez que PGCD ( a^n-1,a^m-1)=a^(PGCD(m,n))-1 | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 19:47 Ven 08 Avr 2011, 19:47 | |
| Bien trop connu, cela dit.
Et je crois qu'il y a même une généralisation à a et b, plutôt que a et 1. | |
|
  | |
darkpseudo
Expert sup
 Nombre de messages : 817 Nombre de messages : 817
Age : 31
Date d'inscription : 31/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 20:39 Ven 08 Avr 2011, 20:39 | |
| En effet c'est un incontournable , mais il serait bien dommage que d'autres ne le sache pas , au moins là tout le monde le connais  | |
|
  | |
Dijkschneier
Expert sup
 Nombre de messages : 1482 Nombre de messages : 1482
Age : 30
Date d'inscription : 12/12/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Ven 08 Avr 2011, 21:09 Ven 08 Avr 2011, 21:09 | |
| La généralisation (avec a et b premiers entre eux) est plus laborieuse cela dit.
EDIT : pas vraiment, en fait.
Dernière édition par Dijkschneier le Mar 12 Avr 2011, 11:10, édité 1 fois | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Avr 2011, 14:07 Sam 09 Avr 2011, 14:07 | |
| - nmo a écrit:
- Problème 88:
Soit a et b deux entiers naturels tel que 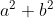 soit premier. soit premier.
Démontrez que l'équattion  n'admet pas de solutions entières. n'admet pas de solutions entières.
Bonne chance. Je procède par absurde: Supposons que l'équation admette deux solutions entières  et  . Alors, on aura:  et  . Et puis: ^2=b^2\text{ et }(\alpha+\beta)^2=a^2\\&\Rightarrow (\alpha.\beta-1)^2+(\alpha+\beta)^2=b^2+a^2\\&\Rightarrow \alpha^2.\beta^2-2\alpha.\beta+1+\alpha^2+\beta^2+2\alpha.\beta=a^2+b^2\\&\Rightarrow \alpha^2.\beta^2+1+\alpha^2+\beta^2=a^2+b^2\\&\Rightarrow (1+\alpha^2)(1+\beta^2)=a^2+b^2\end{align*}) . Et puisque 0 n'est pas une solution à l'équation, alors  et  . Soit  et  ou encore  et  . Ce qui veut bien dire que 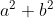 est composé, en contradiction avec les données. On en conclut que l'equation n'admet pas de solutions entières. Sauf erreur. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Avr 2011, 14:18 Sam 09 Avr 2011, 14:18 | |
| Voici un exercice que j'ai inventé: Problème 90:Soit E un ensemble à  entiers non-nuls et inférieurs ou égaux à  . (n est un entiers non nul, m est inférieur à  ). Démontrez qu'il existe au moins deux entiers de l'ensmble E tel que leurs différence vaut  . (((Par exemple, E est l'ensemble composé de 57 (50*1+7) entiers non-nuls et inférieurs ou égaux à 100 (100*1). Le but de l'exercice est de démontrer qu'il existe deux entiers de l'ensemble E tesl que leurs différences vaut 13 (2*7-1).))) Bonne chance.P.S:Je ne dispose pas de la solution du problème, ce ne sont que des remarques qui m'ont guidé à ce résultat. Amusez vous bien à faire cet exercice.
Dernière édition par nmo le Mar 12 Avr 2011, 18:15, édité 2 fois | |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Sam 09 Avr 2011, 23:18 Sam 09 Avr 2011, 23:18 | |
| Bonjour  Voici ma réponse pour le problème 87 On a : 1111≡ 1 [10] ; 1222≡ 2 [10] ; 1333≡ 3 [10] ; 1444≡ 4 [10]
Donc : 1111^n≡ 1 [10] ; 1222^n≡ 2^n [10] ; 1333^n≡ 3^n [10] ; 1444^n≡ 4^n [10]
1111^n+1222^n+1333^n+1444^n ≡ 1+2^n+3^n+4^n [10]
Démonstration par disjonction des cas :
• n= 4k
2^4≡ 6 [10] ; 3^4≡ 1 [10] ; 4^4≡ 6 [10]
2^n≡ 6^k [10] ; 3^n≡ 1 [10] ; 4^n≡ 6^k [10]
1+2^n+3^n+4^n≡ 2(1+6^k) [10] On remarque que : 6² ≡ 6 [10] ; 6^3 ≡ 6 [10] ;
Supposons que 6^k≡ 6 [10] Et démontrons que : 6^k+1 ≡ 6 [10] ∀k∊ℕ
6^(k+1) – 6 = 6(6^k-1) = 6(10k+6-1)= 6Ok+30 = 10(6k+3) = 10 K / K=6k+3
⇒ 6^(k+1) – 6 ≡ 0 [10] ⇒ 6^(k+1)≡ 6 [10]
6^k ≡ 6 [10] ⇒ 2(6^k + 1) ≡ 4 [10] ⇒ 1+2^n+3^n+4^n≡ 4 [10]⇒ 1111^n+1222^n+1333^n+1444^n ≡ 4 [10]
• n= 4k+1
2n= 2.6^k [10] ; 3^n≡ 3 [10] ; 4n≡ 4.6^k [10]
1+2^n+3^n+4^n≡ 4+6.6^k [10] et on a 6^k ≡ 6 [10] ⇒ 6.6^k + 4 ≡ 0 [10]
Donc 1+2^n+3^n+4^n≡ 0 [10] ce qui implique 1111^n+1222^n+1333^n+1444^n ≡ 0 [10]
• n= 4k+2
2^n= 4.6^k [10] ; 3^n≡ -1 [10] ; 4^n≡ 6.6k [10]
1+2^n+3^n+4^n≡ 10.6^k [10]≡ 0 [10] ⇒ 1111^n+1222^n+1333^n+1444^n ≡ 0 [10]
• n= 4k+3
2^n= 8.6^k [10] ; 3^n≡ -3 [10] ; 4^n≡ 4.6^k [10]
1+2^n+3^n+4^n≡ -2+12.6^k [10] ≡ 2(-1+ 6^(k+1)) et on a 6^k ≡ 6 [10] ⇒ 6^(k+1) ≡ 6 [10]⇒ -1 + 6^(k+1)≡ 5 [10] ⇒2(-1+ 6^(k+1))≡ 0 [10]⇒1+2^n+3^n+4^n ≡ 0 [10]⇒ 1111^n+1222^n+1333^n+1444^n ≡ 0 [10] 10|1111^n+1222^n+1333^n+1444^n ⇔ n= 4k+1 ; n= 4k+2 ; n= 4k+3 / k∊ℕ
Cherchons le plus petit nombre n / 1000 ≤ n ≤ 1111
Le plus petit n : n = 4k+1
1000= 4.250 donc n(min)= 4.250+1
n(min)= 1001 Amicalement  | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 10 Avr 2011, 18:05 Dim 10 Avr 2011, 18:05 | |
| Salut scp je veux la solution de cette olimpiades meme si l'ex est facil postez svp la réponse !!
1) Resoudre en IR le systeme :
x^3 + x^2 =2
x^2+ xy +y^2 -y=0
2)soient x et y deux reels strictement positifs tels que x+y=8
Prouvez que (x+1/y)^2 +(y+1/x)^2 >= 289/8
3) Soit ABC un triangle dont l'angle c mesure 60 degre
prouvez que AB/BC +AB/CA >=2
4) Soit ABCD un trapeze de bases [AB] et [CD] dont les diagonales se coupent en O. On désigne par a et b les aires des triangles OAB et OCD.
Calculez l'aire du trapeze en fonction de a et b
Merci
P.s j'aimerai qu on me dise pas que cet exercise est deja fait sinon me dire la page ou il est fai
| |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Dim 10 Avr 2011, 20:05 Dim 10 Avr 2011, 20:05 | |
| jai besoin des reponses Urgent!
| |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Avr 2011, 11:00 Lun 11 Avr 2011, 11:00 | |
| - kaj mima a écrit:
- Bonjour
 Voici ma réponse pour le problème 87 On a : 1111≡ 1 [10] ; 1222≡ 2 [10] ; 1333≡ 3 [10] ; 1444≡ 4 [10] Voici ma réponse pour le problème 87 On a : 1111≡ 1 [10] ; 1222≡ 2 [10] ; 1333≡ 3 [10] ; 1444≡ 4 [10]
Donc : 1111^n≡ 1 [10] ; 1222^n≡ 2^n [10] ; 1333^n≡ 3^n [10] ; 1444^n≡ 4^n [10]
1111^n+1222^n+1333^n+1444^n ≡ 1+2^n+3^n+4^n [10]
Démonstration par disjonction des cas :
• n= 4k
2^4≡ 6 [10] ; 3^4≡ 1 [10] ; 4^4≡ 6 [10]
2^n≡ 6^k [10] ; 3^n≡ 1 [10] ; 4^n≡ 6^k [10]
1+2^n+3^n+4^n≡ 2(1+6^k) [10] On remarque que : 6² ≡ 6 [10] ; 6^3 ≡ 6 [10] ;
Supposons que 6^k≡ 6 [10] Et démontrons que : 6^k+1 ≡ 6 [10] ∀k∊ℕ
6^(k+1) – 6 = 6(6^k-1) = 6(10k+6-1)= 6Ok+30 = 10(6k+3) = 10 K / K=6k+3
⇒ 6^(k+1) – 6 ≡ 0 [10] ⇒ 6^(k+1)≡ 6 [10]
6^k ≡ 6 [10] ⇒ 2(6^k + 1) ≡ 4 [10] ⇒ 1+2^n+3^n+4^n≡ 4 [10]⇒ 1111^n+1222^n+1333^n+1444^n ≡ 4 [10]
• n= 4k+1
2n= 2.6^k [10] ; 3^n≡ 3 [10] ; 4n≡ 4.6^k [10]
1+2^n+3^n+4^n≡ 4+6.6^k [10] et on a 6^k ≡ 6 [10] ⇒ 6.6^k + 4 ≡ 0 [10]
Donc 1+2^n+3^n+4^n≡ 0 [10] ce qui implique 1111^n+1222^n+1333^n+1444^n ≡ 0 [10]
• n= 4k+2
2^n= 4.6^k [10] ; 3^n≡ -1 [10] ; 4^n≡ 6.6k [10]
1+2^n+3^n+4^n≡ 10.6^k [10]≡ 0 [10] ⇒ 1111^n+1222^n+1333^n+1444^n ≡ 0 [10]
• n= 4k+3
2^n= 8.6^k [10] ; 3^n≡ -3 [10] ; 4^n≡ 4.6^k [10]
1+2^n+3^n+4^n≡ -2+12.6^k [10] ≡ 2(-1+ 6^(k+1)) et on a 6^k ≡ 6 [10] ⇒ 6^(k+1) ≡ 6 [10]⇒ -1 + 6^(k+1)≡ 5 [10] ⇒2(-1+ 6^(k+1))≡ 0 [10]⇒1+2^n+3^n+4^n ≡ 0 [10]⇒ 1111^n+1222^n+1333^n+1444^n ≡ 0 [10] 10|1111^n+1222^n+1333^n+1444^n ⇔ n= 4k+1 ; n= 4k+2 ; n= 4k+3 / k∊ℕ
Cherchons le plus petit nombre n / 1000 ≤ n ≤ 1111
Le plus petit n : n = 4k+1
1000= 4.250 donc n(min)= 4.250+1
n(min)= 1001 Amicalement  Oui c'est ça ce que j'avais en tête. Bravo, c'est une belle solution. | |
|
  | |
nmo
Expert sup
 Nombre de messages : 2249 Nombre de messages : 2249
Age : 31
Localisation : Elgara
Date d'inscription : 29/10/2009
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Avr 2011, 11:56 Lun 11 Avr 2011, 11:56 | |
| - darkpseudo a écrit:
- Problème 89 :
Bon voila un lemme très intéressant :
Prouvez que PGCD ( a^n-1,a^m-1)=a^(PGCD(m,n))-1 Puisque le PGCD est strictement positif, il faut ajouter à l'exercice la condition a>1, ainsi que m et n sont des entiers. A moi de le démontrer: Par symétrique des rôles, mon étude comporte deux cas, ou bien n divise m, ou bien m et n sont premiers entre eux. Cas premier:  . On a :m=k\times n) . Démontrons tout d'abord qu'on a  , en effet: &\Rightarrow a^n\equiv1(a^n-1)\\&\Rightarrow (a^n)^k\equiv1^k(a^n-1)\\&\Rightarrow a^{nk}\equiv1(a^n-1)\\&\Rightarrow a^m\equiv1(a^n-1)\\&\Rightarrow a^m-1\equiv0(a^n-1)\end{align*}) . Donc  . On a d'un côté  , alors  . Et d'un autre côté  , alors \wedge(a^m-1)=a^n-1) . On peut affirmer que \wedge(a^m-1)=a^{n\wedge m}-1) . Cas second: m et n sont premiers entre eux. Puisque m et n sont premiers entre eux, on a  et on suppose que n>m. On doit alors démontrer que \wedge(a^m-1)=a-1) . Par ailleurs: :a^k-1=(a-1).(a^{k-1}+a^{k-2}+\cdots+a^2+a^1+a^0)) . Et pour simplifier, on écrit: :a^k-1=(a-1).(\sum_{i=0}^{k-1}a^i)) . Par équivalence, on démontre que .(\sum_{i=0}^{n-1}a^i)\bigg)\wedge\bigg((a-1).(\sum_{i=0}^{m-1}a^i)\bigg)=a-1) . Donc \bigg(\big(\sum_{i=0}^{n-1}a^i\big)\wedge\big(\sum_{i=0}^{m-1}a^i\big)\bigg)=a-1) . Soit \wedge\big(\sum_{i=0}^{m-1}a^i\big)=1) . On utilise pour démontrer ce fait, l'algorithme d'Euclide: Puisque n>m, on pose n=m+r tel que r est strictement positif et r est inférieur à m. Il s'agit là de la division euclédienne de n par m. On a: +a^{r}+a^{r-1}+a^{r-2}+\cdots+a^2+a^1+a^0\end{align*}) . Soit +(\sum_{i=0}^{r-1}a^i)) . Ainsi: \wedge\big(\sum_{i=0}^{m-1}a^i\big)=\big(\sum_{i=0}^{m-1}a^i\big)\wedge\big(\sum_{i=0}^{r-1}a^i\big)) . On itère ce processus plusieurs fois, jusqu'à un reste qui vaut 1, car PGCD(m,n)=1 Appelon ce reste t (t=1), et le reste qui le précède s. On aura: \wedge\big(\sum_{i=0}^{m-1}a^i\big)=\big(\sum_{i=0}^{s-1}a^i\big)\wedge\big(\sum_{i=0}^{t-1}a^i\big)) . Avec  . Et par conséquent, \wedge\big(\sum_{i=0}^{m-1}a^i\big)=\big(\sum_{i=0}^{s-1}a^i\big)\wedge1) . Soit \wedge\big(\sum_{i=0}^{m-1}a^i\big)=1) . CQFD. Sauf erreur. J'attends une confirmation. | |
|
  | |
amigo-6
Maître
 Nombre de messages : 108 Nombre de messages : 108
Age : 28
Localisation : Fes
Date d'inscription : 09/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Avr 2011, 12:43 Lun 11 Avr 2011, 12:43 | |
| J'atten une réponse a mon olimpiade svp
| |
|
  | |
kaj mima
Expert grade1
 Nombre de messages : 422 Nombre de messages : 422
Age : 30
Localisation : Tétouan
Date d'inscription : 05/03/2011
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Avr 2011, 12:52 Lun 11 Avr 2011, 12:52 | |
| | |
|
  | |
Mehdi.O
Expert sup
 Nombre de messages : 815 Nombre de messages : 815
Age : 29
Localisation : Rabat
Date d'inscription : 23/07/2010
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  Lun 11 Avr 2011, 13:58 Lun 11 Avr 2011, 13:58 | |
| En attendant, je postes cette petite inégalité : Problème 91 :Soit x,y,z des réels strictement positives. Prouvez que : 
Dernière édition par Mehdi.O le Lun 11 Avr 2011, 17:25, édité 1 fois | |
|
  | |
Contenu sponsorisé
 |  Sujet: Re: Préparations aux olympiades de première (2010-2011) Sujet: Re: Préparations aux olympiades de première (2010-2011)  | |
| |
|
  | |
| | Préparations aux olympiades de première (2010-2011) |  |
|
